Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-24T22:49:19.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of the Prandtl model for katabatic slope flows

Published online by Cambridge University Press:  28 February 2019

Cheng-Nian Xiao Open the ORCID record for Cheng-Nian Xiao [Opens in a new window]  and
Inanc Senocak Open the ORCID record for Inanc Senocak [Opens in a new window]
Cheng-Nian Xiao
Affiliation:
Department of Mechanical Engineering and Materials Science, University of Pittsburgh, Pittsburgh, PA 15261, USA
Inanc Senocak*
Affiliation:
Department of Mechanical Engineering and Materials Science, University of Pittsburgh, Pittsburgh, PA 15261, USA
*
†Email address for correspondence: senocak@pitt.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the stability of the Prandtl model for katabatic slope flows using both linear stability theory and direct numerical simulations. Starting from Prandtl’s analytical solution for uniformly cooled laminar slope flows, we use linear stability theory to identify the onset of instability and features of the most unstable modes. Our results show that the Prandtl model for parallel katabatic slope flows is prone to transverse and longitudinal modes of instability. The transverse mode of instability manifests itself as stationary vortical flow structures aligned in the along-slope direction, whereas the longitudinal mode of instability emerges as waves propagating in the base-flow direction. Beyond the stability limits, these two modes of instability coexist and form a complex flow structure crisscrossing the plane of flow. The emergence of a particular form of these instabilities depends strongly on three dimensionless parameters, which are the slope angle, the Prandtl number and a newly introduced stratification perturbation parameter, which is proportional to the relative importance of the disturbance to the background stratification due to the imposed surface buoyancy flux. We demonstrate that when this parameter is sufficiently large, then the stabilising effect of the background stratification can be overcome. For shallow slopes, the transverse mode of instability emerges despite meeting the Miles–Howard stability criterion of 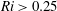$Ri>0.25$. At steep slope angles, slope flow can remain linearly stable despite attaining Richardson numbers as low as 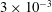$3\times 10^{-3}$.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Geophysical and Geological Flows: Stratified flows
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 865 , 25 April 2019 , R2
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Candelier, J., Le Dizès, S. & Millet, C. 2011 Shear instability in a stratified fluid when shear and stratification are not aligned. J. Fluid Mech. 685, 191–201.10.1017/jfm.2011.306Google Scholar
Chen, J., Bai, Y. & Le Dizès, S. 2016 Instability of a boundary layer flow on a vertical wall in a stably stratified fluid. J. Fluid Mech. 795, 262–277.10.1017/jfm.2016.202Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability, 2nd edn. Cambridge University Press.10.1017/CBO9780511616938Google Scholar
Facchini, G., Favier, B., Le Gal, P., Wang, M. & Le Bars, M. 2018 The linear instability of the stratified plane Couette flow. J. Fluid Mech. 853, 205–234.10.1017/jfm.2018.556Google Scholar
Fedorovich, E. & Shapiro, A. 2009 Structure of numerically simulated katabatic and anabatic flows along steep slopes. Acta Geophys. 57 (4), 981–1010.10.2478/s11600-009-0027-4Google Scholar
Görtler, H. 1959 Über eine Analogie zwischen den Instabilitäten laminarer Grenzschichtströmungen an konkaven Wänden und an erwärmten Wänden. Ing.-Arch. 28 (1), 71–78.10.1007/BF00536101Google Scholar
Jacobsen, D. A. & Senocak, I. 2013 Multi-level parallelism for incompressible flow computations on GPU clusters. Parallel Comput. 39 (1), 1–20.10.1016/j.parco.2012.10.002Google Scholar
Kaminski, A. K., Caulfield, C. P. & Taylor, J. R. 2017 Nonlinear evolution of linear optimal perturbations of strongly stratified shear layers. J. Fluid Mech. 825, 213–244.10.1017/jfm.2017.396Google Scholar
Kolář, V. 2007 Vortex identification: new requirements and limitations. Intl J. Heat Fluid Flow 28 (4), 638–652.10.1016/j.ijheatfluidflow.2007.03.004Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10 (4), 496–508.10.1017/S0022112061000305Google Scholar
Miller, J. R. & Gage, K. S. 1972 Prandtl number dependence of the stability of a stratified free shear layer. Phys. Fluids 15 (5), 723–725.10.1063/1.1693973Google Scholar
Prandtl, L. 1942 Führer durch die Strömungslehre. Vieweg und Sohn.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.10.1007/978-1-4613-0185-1Google Scholar
Shapiro, A. & Fedorovich, E. 2004 Unsteady convectively driven flow along a vertical plate immersed in a stably stratified fluid. J. Fluid Mech. 498, 333–352.10.1017/S0022112003006803Google Scholar
Shapiro, A. & Fedorovich, E. 2014 A boundary-layer scaling for turbulent katabatic flow. Boundary-Layer Meteorol. 153 (1), 1–17.10.1007/s10546-014-9933-3Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223 (605–615), 289–343.10.1098/rsta.1923.0008Google Scholar
Umphrey, C., DeLeon, R. & Senocak, I. 2017 Direct numerical simulation of turbulent katabatic slope flows with an immersed boundary method. Boundary-Layer Meteorol. 164 (3), 367–382.10.1007/s10546-017-0252-3Google Scholar