Article contents
Separation length scaling for dual-incident shock wave–turbulent boundary layer interactions with different shock wave distances
Published online by Cambridge University Press: 30 March 2023
Abstract
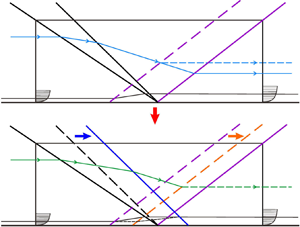
In this study, the length scaling for the boundary layer separation induced by two incident shock waves is experimentally and analytically investigated. The experiments are performed in a Mach 2.73 flow. A double-wedge shock generator with two deflection angles ( $\alpha _1$ and
$\alpha _1$ and  $\alpha _2$) is employed to generate two incident shock waves. Two deflection angle combinations with an identical total deflection angle are adopted: (
$\alpha _2$) is employed to generate two incident shock waves. Two deflection angle combinations with an identical total deflection angle are adopted: ( $\alpha _1 = 7^\circ$,
$\alpha _1 = 7^\circ$,  $\alpha _2 = 5^\circ$) and (
$\alpha _2 = 5^\circ$) and ( $\alpha _1 = 5^\circ$,
$\alpha _1 = 5^\circ$,  $\alpha _2 = 7^\circ$). For each deflection angle combination, the flow features of the dual-incident shock wave–turbulent boundary layer interactions (dual-ISWTBLIs) under five shock wave distance conditions are examined via schlieren photography, wall-pressure measurements and surface oil-flow visualisation. The experimental results show that the separation point moves downstream with increasing shock wave distance (
$\alpha _2 = 7^\circ$). For each deflection angle combination, the flow features of the dual-incident shock wave–turbulent boundary layer interactions (dual-ISWTBLIs) under five shock wave distance conditions are examined via schlieren photography, wall-pressure measurements and surface oil-flow visualisation. The experimental results show that the separation point moves downstream with increasing shock wave distance ( $d$). For the dual-ISWTBLIs exhibiting a coupling separation state, the upstream interaction length (
$d$). For the dual-ISWTBLIs exhibiting a coupling separation state, the upstream interaction length ( $L_{int}$) of the separation region approximately linearly decreases with increasing
$L_{int}$) of the separation region approximately linearly decreases with increasing  $d$, and the decrease rate of
$d$, and the decrease rate of  $L_{int}$ with
$L_{int}$ with  $d$ increases with the second deflection angle under the condition of an identical total deflection angle. Based on control volume analysis of mass and momentum conservations, the relation between
$d$ increases with the second deflection angle under the condition of an identical total deflection angle. Based on control volume analysis of mass and momentum conservations, the relation between  $L_{int}$ and
$L_{int}$ and  $d$ is analytically determined to be approximately linear for the dual-ISWTBLIs with a coupling separation region, and the slope of the linear relation obtained analytically agrees well with that obtained experimentally. Furthermore, a prediction method for
$d$ is analytically determined to be approximately linear for the dual-ISWTBLIs with a coupling separation region, and the slope of the linear relation obtained analytically agrees well with that obtained experimentally. Furthermore, a prediction method for  $L_{int}$ of the dual-ISWTBLIs with a coupling separation region is proposed, and the relative error of the predicted
$L_{int}$ of the dual-ISWTBLIs with a coupling separation region is proposed, and the relative error of the predicted  $L_{int}$ in comparison with the experimental result is
$L_{int}$ in comparison with the experimental result is  $\sim$10 %.
$\sim$10 %.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 4
- Cited by





