1. Introduction
Combustors in gas turbine engines present two sources of noise associated with the combustion process (Dowling & Mahmoudi Reference Dowling and Mahmoudi2015; Ihme Reference Ihme2017; Tam et al. Reference Tam, Bake, Hultgren and Poinsot2019): (i) direct combustion noise and (ii) indirect combustion noise. The first component designates the generation of pressure fluctuations arising from unsteady heat released by the flame. Unsteady combustion also generates flow perturbations in the form of temperature, vorticity and mixture-composition inhomogeneities. These perturbations, which are silent while advected by a uniform flow (Chu & Kovásznay Reference Chu and Kovásznay1958), generate further sound when accelerated/decelerated (Marble & Candel Reference Marble and Candel1977; Bake et al. Reference Bake, Richter, Mühlbauer, Kings, Röhle, Thiele and Noll2009). This second source of noise is termed indirect combustion noise and can be further classified into three subcomponents depending on the flow perturbation causing it: (i) entropy noise (Marble & Candel Reference Marble and Candel1977; Bake et al. Reference Bake, Richter, Mühlbauer, Kings, Röhle, Thiele and Noll2009), (ii) vortex noise (Kings & Bake Reference Kings and Bake2010) and (iii) compositional noise (Strahle Reference Strahle1976; Magri, O'Brien & Ihme Reference Magri, O'Brien and Ihme2016; Ihme Reference Ihme2017). Entropy noise is believed to be the dominant component (Morgans & Duran Reference Morgans and Duran2016) and, consequently, has been the focus of most research on indirect combustion noise. The present paper deals with entropy noise as the main component of indirect combustion noise.
Indirect combustion noise contributes to the total exhaust noise of aeroengines, via the downstream propagating component (Leyko, Nicoud & Poinsot Reference Leyko, Nicoud and Poinsot2009; Duran et al. Reference Duran, Moreau, Nicoud, Livebardon, Bouty and Poinsot2014; Tam, Li & Schuster Reference Tam, Li and Schuster2016). It also modifies the stability of the combustor, via the upstream propagating component (Goh & Morgans Reference Goh and Morgans2013; Morgans & Duran Reference Morgans and Duran2016). Thermoacoustic instabilities (Candel Reference Candel2002; Lieuwen Reference Lieuwen2003) arise from the two-way coupling between acoustic disturbances and heat release within the combustion chamber. They lead to large amplitude self-excited oscillations which have the potential to cause severe structural damage to the combustion chamber and the turbine. Therefore, predicting and suppressing combustion instabilities at an early design stage is a priority. To correctly assess the stability of a combustor, indirect combustion noise generated by flow inhomogeneities going through the nozzle guide vanes (NGVs) at the exit of the combustion chamber must be accurately described.
The generation of entropy noise comprises three stages that can be studied and modelled separately. First, incompressible temperature fluctuations, the so-called entropy waves, are generated at the flame by an unsteady heat release rate (Bragg Reference Bragg1963; Strahle Reference Strahle1978; Dowling Reference Dowling1995). Karimi, Brear & Moase (Reference Karimi, Brear and Moase2008) showed that one-dimensional, non-diffusive flows with heat communication behave as low-pass filters when excited by an unsteady heat release rate: an effective cutoff frequency exists, below which significant entropy generation occurs and above which entropy generation diminishes. Yoon (Reference Yoon2020) found that the entropic cutoff frequency is inversely proportional to the flame residence time. Entropy generation has been the subject of recent investigations using low-order models (Chen, Bomberg & Polifke Reference Chen, Bomberg and Polifke2016), numerical simulations (Semlitsch et al. Reference Semlitsch, Hynes, Langella, Swaminathan and Dowling2019) and experimental measurements (Wang et al. Reference Wang, Liu, Wang, Li and Qi2019; Weilenmann et al. Reference Weilenmann, Doll, Bombach, Blondé, Ebi, Xiong and Noiray2020a).
Second, entropy waves advect towards the combustor exit and are dissipated and dispersed in the process (Sattelmayer Reference Sattelmayer2003; Morgans, Goh & Dahan Reference Morgans, Goh and Dahan2013). At low frequencies, diffusion was found to be negligible and shear dispersion arising from the velocity profile was found to be the main mechanism in the decay of entropy waves (Morgans et al. Reference Morgans, Goh and Dahan2013; Giusti et al. Reference Giusti, Worth, Mastorakos and Dowling2017; Xia et al. Reference Xia, Duran, Morgans and Han2018). Fattahi, Hosseinalipour & Karimi (Reference Fattahi, Hosseinalipour and Karimi2017) studied numerically the dissipation of entropy waves in a turbulent channel flow and showed that the high-frequency components are always strongly damped. This result was further supported by experimental results in a circular duct (Hosseinalipour et al. Reference Hosseinalipour, Fattahi, Khalili, Tootoonchian and Karimi2020). The latter study also showed that the components of the entropy wave with convective wavelengths longer than the duct-diameter remain highly coherent throughout the duct, which supports the use of one-dimensional entropy noise models. At higher frequencies, the spatial correlation of the waves was lost. Christodoulou et al. (Reference Christodoulou, Karimi, Cammarano, Paul and Navarro-Martinez2020) developed a low-order model that accounts for variable shapes and amplitudes of entropy waves. The recent experimental work of Weilenmann, Xiong & Noiray (Reference Weilenmann, Xiong and Noiray2020b) suggests the need for low-order models that also describe dispersion effects owing to turbulent coherent structures. This was shown numerically by Xia et al. (Reference Xia, Duran, Morgans and Han2018).
A common conclusion of the studies on both generation and transport is the low-frequency nature of the waves reaching the end of the combustor. In a recent experiment by Greifenstein et al. (Reference Greifenstein, Heinze, Willert, Voigt, Zedda, Richter and Dreizler2020), the combined effect of both phenomena in a realistic combustor was studied. The study revealed the strong influence of a central precessing vortex core on the entropy profiles measured at the exit of the combustor.
Finally, the entropy waves that reach the exit of the combustor are accelerated and generate noise in the process. In gas turbines and aeroengines, the acceleration occurs through the turbine blade rows, while in lab-scale experiments, the acceleration is often provided by a nozzle flow. The case of interest for this paper is the former, but for the sake of completeness we offer a brief review of the state-of-the-art of entropy noise generated by nozzle flows. The seminal theory of Marble & Candel (Reference Marble and Candel1977) presents analytical transfer functions for the entropy noise generated in the zero-frequency limit assuming a quasi-one-dimensional and isentropic flow. This model was extended to higher frequencies by Moase, Brear & Manzie (Reference Moase, Brear and Manzie2007), Giauque, Huet & Clero (Reference Giauque, Huet and Clero2012), Stow, Dowling & Hynes (Reference Stow, Dowling and Hynes2002) and Goh & Morgans (Reference Goh and Morgans2011). Finally, the Magnus expansion of Duran & Moreau (Reference Duran and Moreau2013) generalised the model to be valid at any frequency. This was later extended to circumferential waves by Duran & Morgans (Reference Duran and Morgans2015). In the mid-frequencies, three-dimensional effects become apparent and must be described by the model (Emmanuelli et al. Reference Emmanuelli, Zheng, Huet, Giauque, Le Garrec and Ducruix2020; Huet, Emmanuelli & Le Garrec Reference Huet, Emmanuelli and Le Garrec2020). Further extensions of the quasi-one-dimensional theory include nonlinear effects (Huet & Giauque Reference Huet and Giauque2013), compositional inhomogeneities (Magri et al. Reference Magri, O'Brien and Ihme2016; Magri Reference Magri2017) and non-isentropic effects (De Domenico, Rolland & Hochgreb Reference De Domenico, Rolland and Hochgreb2019).
We now turn our attention to the entropy noise generated by blades. To solve this problem, Cumpsty & Marble (Reference Cumpsty and Marble1977b, Reference Cumpsty and Marblea) proposed an actuator disk method which considers flow fluctuations to be plane both upstream and downstream of the blade row undergoing a discontinuous jump of strength through it. This approach is based on the assumption that the entropy wavelength is large compared to the length of the blade and neglects the details of the mean flow (compact assumption). Mishra & Bodony (Reference Mishra and Bodony2013) and Leyko et al. (Reference Leyko, Duran, Moreau, Nicoud and Poinsot2014) compared the results of this theory with numerical simulations, which showed that disk actuator theory is only valid at low frequencies. Despite this limitation, disk actuator theory represents the current state-of-the-art for predicting the sound field generated by the interaction of entropy waves with blades. The theory was further extended to rotor cascades by Bauerheim et al. (Reference Bauerheim, Duran, Livebardon, Wang, Moreau and Poinsot2016).
In parallel to disk actuator models, a theory of entropy noise was developed using acoustic analogies combined with the Green's function method (Morfey Reference Morfey1973; Ffowcs Williams & Howe Reference Ffowcs Williams and Howe1975; Howe Reference Howe1975, Reference Howe2010; Yang, Guzmán-Iñigo & Morgans unpublished observations). This approach however is intrinsically limited to low-Mach-number flows, with entropy noise being important in the high-Mach-number regime. As an alternative to acoustic analogies, Bodony (Reference Bodony2009) proposed a model based on rapid distortion theory (Goldstein Reference Goldstein1978) and the Green's function method. Rapid distortion theory, which recast the problem as an inhomogeneous wave equation with a source term, is an exact rearrangement of the linearised compressible Euler equations. It has been widely used to describe high-frequency vortical noise for isolated aerofoils (Kerschen & Myers Reference Kerschen and Myers1987; Tsai Reference Tsai1992; Myers & Kerschen Reference Myers and Kerschen1995, Reference Myers and Kerschen1997) and cascades (Peake & Kerschen Reference Peake and Kerschen1997, Reference Peake and Kerschen2004). The aforementioned models account for entropy perturbations, but the low-frequency nature of entropy noise renders them of no use in practice. Recently, Baddoo & Ayton (Reference Baddoo and Ayton2020) developed a solution for cascades of blades valid at low-to-moderate frequencies. This approach was extended to account for compositional perturbations by Guzmán-Iñigo et al. (Reference Guzmán-Iñigo, Baddoo, Ayton and Morgans2019). The Baddoo and Ayton model assumes that the mean flow is a small perturbation to a uniform flow. This assumption, which is valid for compressor and fan cascades, is too restrictive for turbine cascades where the favourable pressure gradient allows for larger angles of attack, cambers and thickness of the aerofoils.
In this paper, we build on Bodony's approach and combine rapid distortion theory with a compact Green's function (Howe Reference Howe1975). Bodony (Reference Bodony2009) assumed the Mach number to be small and neglected the effect of the mean flow in the propagation of sound. The model was then used to propose a qualitative interpretation of the underlying physical mechanism, but no quantitative validation was provided. The contributions of this paper are twofold. First, we introduce the Born approximation (Snieder & Van Wijk Reference Snieder and Van Wijk2015, Ch. 23) to simplify the governing equations. This simplification allows a Green's function to be obtained that, using a Lorentz-type transformation, accounts for the effect of the mean flow even at subsonic Mach numbers close to unity. For thin aerofoils, this solution is valid for low-to-moderate frequencies and any subsonic Mach number. If the aerofoil is thicker or its camber or angle of attack is large, the proposed solution is still valid at the expense of the range of validity in frequency and Mach number. Second, we simplify the source term using thin-aerofoil theory and obtain a closed form solution by numerically integrating the different terms. This solution is compared with numerical simulations of the Euler equations, and show a very good agreement for a wide range of frequencies and Mach numbers.
This paper is organised as follows. In § 2, we introduce the governing equations of the problem. The acoustic propagation operator is simplified and an integral solution is proposed using the compact Green's function method in § 3. In § 4, the source term is also simplified using thin-aerofoil theory and a solution is obtained for a symmetric Joukowsky aerofoil in § 5. A summary of the results and conclusions are given in § 6.
2. Problem formulation
2.1. Configuration and governing equations
We consider the flow past a two-dimensional single aerofoil of semi-chord ![]() $b = c/2,$ as sketched in figure 1. The flow is taken to be inviscid, non-heat-conducting and a compressible perfect gas. Neglecting volumetric forces, as well as thermal and mass diffusion the conservation of mass, momentum and energy can be written, respectively, as
$b = c/2,$ as sketched in figure 1. The flow is taken to be inviscid, non-heat-conducting and a compressible perfect gas. Neglecting volumetric forces, as well as thermal and mass diffusion the conservation of mass, momentum and energy can be written, respectively, as
where ![]() $\rho$ is the density,
$\rho$ is the density, ![]() $p$ is the pressure,
$p$ is the pressure, ![]() $\boldsymbol {U}$ is the velocity,
$\boldsymbol {U}$ is the velocity, ![]() $s$ is the specific entropy and
$s$ is the specific entropy and ![]() $t$ is the time.
$t$ is the time.

Figure 1. Aerofoil of semi-chord ![]() $b$ at incidence angle
$b$ at incidence angle ![]() $\alpha$ encountering a convected entropy disturbance.
$\alpha$ encountering a convected entropy disturbance.
We suppose that the flow upstream consists of a uniform component of velocity ![]() $U_{\infty },$ density
$U_{\infty },$ density ![]() $\rho _{\infty }$ and speed of sound
$\rho _{\infty }$ and speed of sound ![]() $a_{\infty },$ on which there is superimposed a small unsteady motion. Consequently, the flow can be decomposed into a steady mean, denoted by
$a_{\infty },$ on which there is superimposed a small unsteady motion. Consequently, the flow can be decomposed into a steady mean, denoted by ![]() $(\boldsymbol {\cdot })_0$, and a perturbation component, denoted by
$(\boldsymbol {\cdot })_0$, and a perturbation component, denoted by ![]() $(\boldsymbol {\cdot })'.$
$(\boldsymbol {\cdot })'.$
The equations governing the mean flow are
The mean flow is also assumed homentropic, i.e. ![]() $s_0=0,$ and irrotational, i.e.
$s_0=0,$ and irrotational, i.e. ![]() ${\boldsymbol {\nabla } \times \boldsymbol {U}_0=0}$. Under the irrotational assumption, there exists a potential function such that
${\boldsymbol {\nabla } \times \boldsymbol {U}_0=0}$. Under the irrotational assumption, there exists a potential function such that ![]() $\boldsymbol {U}_{0}=\boldsymbol {\nabla } \varPhi$. Furthermore, and because the flow is two-dimensional, we can define a compressible stream function
$\boldsymbol {U}_{0}=\boldsymbol {\nabla } \varPhi$. Furthermore, and because the flow is two-dimensional, we can define a compressible stream function ![]() $\varPsi$ as
$\varPsi$ as
where the factor ![]() $\beta _{\infty }=\sqrt {1-M^{2}_{\infty }}$
$\beta _{\infty }=\sqrt {1-M^{2}_{\infty }}$ ![]() $(M_{\infty }=U_{\infty }/a_{\infty })$ corresponds to a Prandtl–Glauert transformation (Ashley & Landahl Reference Ashley and Landahl1985) and
$(M_{\infty }=U_{\infty }/a_{\infty })$ corresponds to a Prandtl–Glauert transformation (Ashley & Landahl Reference Ashley and Landahl1985) and ![]() $\boldsymbol {e_3}$ is the unit vector perpendicular to the
$\boldsymbol {e_3}$ is the unit vector perpendicular to the ![]() $x_1 - x_2$ plane.
$x_1 - x_2$ plane.
We assume that small-amplitude entropic disturbances are superimposed on the uniform flow (infinitely far upstream). These disturbances are convected downstream by the mean flow and interact with the aerofoil, which produces sound. Similar approaches have been employed (Myers Reference Myers1987; Tsai Reference Tsai1992; Myers & Kerschen Reference Myers and Kerschen1995, Reference Myers and Kerschen1997) in modelling gust–blade interaction. Neglecting squares of small quantities and subtracting out the mean flow equations, we obtain that the dynamics of the perturbation part is governed by
where ![]() $\textrm {D}_0/\textrm {D}t = \partial /\partial t + \boldsymbol {U}_0 \boldsymbol {\cdot } \boldsymbol {\nabla }$ is the material derivative with respect to the local mean flow. The perturbation density, pressure and entropy are related by the Gibbs equation, which leads to
$\textrm {D}_0/\textrm {D}t = \partial /\partial t + \boldsymbol {U}_0 \boldsymbol {\cdot } \boldsymbol {\nabla }$ is the material derivative with respect to the local mean flow. The perturbation density, pressure and entropy are related by the Gibbs equation, which leads to
where ![]() $\gamma$ is the ratio of the specific heat capacities of the gas at constant pressure
$\gamma$ is the ratio of the specific heat capacities of the gas at constant pressure ![]() $c_p$ and constant volume
$c_p$ and constant volume ![]() $c_v,$ i.e.
$c_v,$ i.e. ![]() $\gamma =c_p/c_v.$
$\gamma =c_p/c_v.$
2.2. Rapid distortion theory formulation
The generalisation of rapid distortion theory proposed by Goldstein (Reference Goldstein1978) provides a well-suited framework for solving (2.4). Goldstein (Reference Goldstein1978) showed that the analysis of the perturbation dynamics can be reduced to solving a single inhomogeneous wave equation by introducing the following splitting of the perturbation velocity and pressure:
and
The perturbation velocity is represented as the sum of a component that is the gradient of an acoustic potential ![]() $\phi ,$ a homogeneous component
$\phi ,$ a homogeneous component ![]() $\boldsymbol {u}^{(H)}$ and a term proportional to the perturbation entropy
$\boldsymbol {u}^{(H)}$ and a term proportional to the perturbation entropy ![]() $s'$. The homogeneous component,
$s'$. The homogeneous component, ![]() $\boldsymbol {u}^{(H)},$ satisfies a modified form of the linearised momentum equation:
$\boldsymbol {u}^{(H)},$ satisfies a modified form of the linearised momentum equation:
and ![]() $s'$ satisfies the energy equation (2.4c). These equations can be integrated exactly using the method of characteristics if appropriate boundary conditions are provided (see § 2.3).
$s'$ satisfies the energy equation (2.4c). These equations can be integrated exactly using the method of characteristics if appropriate boundary conditions are provided (see § 2.3).
To determine the acoustic potential ![]() $\phi ,$ (2.6), (2.7) and (2.5) are substituted into (2.4a) to obtain the following inhomogeneous, convective wave equation:
$\phi ,$ (2.6), (2.7) and (2.5) are substituted into (2.4a) to obtain the following inhomogeneous, convective wave equation:
subject to boundary conditions
where ![]() $\varSigma$ is the surface of the aerofoil and
$\varSigma$ is the surface of the aerofoil and ![]() $a_0$ is the local speed of sound of the mean flow.
$a_0$ is the local speed of sound of the mean flow.
The decomposition given by (2.6) and (2.7) greatly simplifies the problem: a coupled system of four partial differential equations (PDEs) is transformed into three fully decoupled PDEs ((2.8) and (2.4c)) together with a wave equation (2.9) coupled to the aforementioned ones only through the source term. The former equations can be integrated analytically, as explained in § 2.3, and an approximated solution to the latter is proposed in § 3.
2.3. Time-periodic entropy fluctuations
Equations (2.8) and (2.4c) can be integrated exactly using the method of characteristics if appropriate boundary conditions are provided. Here, we set a time-periodic entropic perturbation far upstream of the form:
where ![]() $k_1$ and
$k_1$ and ![]() $k_2$ are the wavenumbers of the perturbation in
$k_2$ are the wavenumbers of the perturbation in ![]() $x_1$ and
$x_1$ and ![]() $x_2,$ respectively, and
$x_2,$ respectively, and ![]() $\omega$ is the angular frequency. The relation
$\omega$ is the angular frequency. The relation ![]() $k_1 = \omega /U_{\infty }$ is satisfied. Equation (2.4c) can be integrated to yield:
$k_1 = \omega /U_{\infty }$ is satisfied. Equation (2.4c) can be integrated to yield:
where ![]() $\boldsymbol {k}= ( k_1, k_2 )^{\top }$ and
$\boldsymbol {k}= ( k_1, k_2 )^{\top }$ and ![]() $\boldsymbol {X}=( X_{\varPhi }, X_{\varPsi } )^{\top }$ are vectors containing, respectively, the entropy wavenumbers and mean-flow Lagrangian coordinates:
$\boldsymbol {X}=( X_{\varPhi }, X_{\varPsi } )^{\top }$ are vectors containing, respectively, the entropy wavenumbers and mean-flow Lagrangian coordinates:
with
as the drift function and ![]() $U_0$ is the magnitude of the velocity vector
$U_0$ is the magnitude of the velocity vector ![]() $\boldsymbol {U}_0.$ Note that the drift function
$\boldsymbol {U}_0.$ Note that the drift function ![]() $g$ is singular along any streamline passing through a stagnation point.
$g$ is singular along any streamline passing through a stagnation point.
Additionally, we assume that the disturbances of the mean flow far upstream of the body are purely entropic (![]() $\boldsymbol {u}'_{\infty }=0).$ Using this assumption, the homogeneous components of the perturbation velocity,
$\boldsymbol {u}'_{\infty }=0).$ Using this assumption, the homogeneous components of the perturbation velocity, ![]() $\boldsymbol {u}^{(H)}$, are directly obtained in Lagrangian coordinates (Kerschen & Balsa Reference Kerschen and Balsa1981) as
$\boldsymbol {u}^{(H)}$, are directly obtained in Lagrangian coordinates (Kerschen & Balsa Reference Kerschen and Balsa1981) as
with ![]() $u^{(H)}_t$ and
$u^{(H)}_t$ and ![]() $u^{(H)}_n$ denoting the velocity components parallel and normal to a streamline, respectively.
$u^{(H)}_n$ denoting the velocity components parallel and normal to a streamline, respectively.
The source term of (2.9) can now be obtained as
where
 $$\begin{align} \hat S(\varPhi,
\varPsi; \omega) &= \frac{A_s}{2} \left[{-}2
\frac{U_{\infty}^{2}}{U_0}\frac{\partial {U_0}}{\partial
{\varPhi}} + 2 \beta_{\infty}^{2}\frac{\rho_0
U_0^{2}}{\rho_{\infty}^{2}} \frac{\partial
{\rho_0}}{\partial {\varPsi}}\frac{\partial {g}}{\partial
{\varPsi}} \right. + \beta_{\infty}^{2}\frac{\rho_0^{2}
U_0^{2}}{\rho_{\infty}^{2}} \frac{\partial
{{}^{2}g}}{\partial {\varPsi^{2}}} + \mathrm{i}
k_1 {U_{\infty}}\nonumber\\ &\quad \times \left( \frac{U_{\infty}^{2}}{U_0^{2}} -
1 + \beta_{\infty}^{2}\frac{\rho_0^{2}
U_0^{2}}{\rho_{\infty}^{2}U_{\infty}^{2}}\frac{\partial
{g}}{\partial {\varPsi}} \frac{\partial {g}}{\partial
{\varPsi}} \right) + \mathrm{i} k_2
\beta_{\infty}\frac{\rho_0^{2}
U_0^{2}}{\rho_{\infty}^{2}{U_{\infty}}}\frac{\partial
{g}}{\partial {\varPsi}} \left. \vphantom{\frac{\rho_0^{2}
U_0^{2}}{{M_{\infty}}}\frac{\partial {g}}{\partial
{\varPsi}}} \right] \exp({\mathrm{i} \boldsymbol{k}
\boldsymbol{\cdot} \boldsymbol{X}}).
\end{align}$$
$$\begin{align} \hat S(\varPhi,
\varPsi; \omega) &= \frac{A_s}{2} \left[{-}2
\frac{U_{\infty}^{2}}{U_0}\frac{\partial {U_0}}{\partial
{\varPhi}} + 2 \beta_{\infty}^{2}\frac{\rho_0
U_0^{2}}{\rho_{\infty}^{2}} \frac{\partial
{\rho_0}}{\partial {\varPsi}}\frac{\partial {g}}{\partial
{\varPsi}} \right. + \beta_{\infty}^{2}\frac{\rho_0^{2}
U_0^{2}}{\rho_{\infty}^{2}} \frac{\partial
{{}^{2}g}}{\partial {\varPsi^{2}}} + \mathrm{i}
k_1 {U_{\infty}}\nonumber\\ &\quad \times \left( \frac{U_{\infty}^{2}}{U_0^{2}} -
1 + \beta_{\infty}^{2}\frac{\rho_0^{2}
U_0^{2}}{\rho_{\infty}^{2}U_{\infty}^{2}}\frac{\partial
{g}}{\partial {\varPsi}} \frac{\partial {g}}{\partial
{\varPsi}} \right) + \mathrm{i} k_2
\beta_{\infty}\frac{\rho_0^{2}
U_0^{2}}{\rho_{\infty}^{2}{U_{\infty}}}\frac{\partial
{g}}{\partial {\varPsi}} \left. \vphantom{\frac{\rho_0^{2}
U_0^{2}}{{M_{\infty}}}\frac{\partial {g}}{\partial
{\varPsi}}} \right] \exp({\mathrm{i} \boldsymbol{k}
\boldsymbol{\cdot} \boldsymbol{X}}).
\end{align}$$
The time-harmonic dependence of the source term and boundary conditions of (2.9) allow us to write a solution in the form ![]() $\phi (\boldsymbol {x},t) = \hat \phi (\boldsymbol {x}) \exp {( -\mathrm {i} \omega t )}.$ Introducing now the acoustic wavenumber
$\phi (\boldsymbol {x},t) = \hat \phi (\boldsymbol {x}) \exp {( -\mathrm {i} \omega t )}.$ Introducing now the acoustic wavenumber ![]() $\kappa _0=\omega /a_0$ and local Mach number
$\kappa _0=\omega /a_0$ and local Mach number ![]() $\boldsymbol {M}_0=\boldsymbol {U}_0/a_0,$ this equation can be rewritten as
$\boldsymbol {M}_0=\boldsymbol {U}_0/a_0,$ this equation can be rewritten as
with
 $$\begin{gather} \mathcal{L}_{0}\left(\hat \phi \right) = \boldsymbol{\nabla} \hat \phi \boldsymbol{\cdot} \left(-\boldsymbol{M}_0 \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{M}_0 + \boldsymbol{\nabla} \ln \rho_0 + \boldsymbol{M}_0( \boldsymbol{M}_0 \boldsymbol{\cdot} \boldsymbol{\nabla} \ln a_0) \right)\nonumber\\ +\, \mathrm{i} \hat \phi \left( \boldsymbol{M}_0\boldsymbol{\cdot} \boldsymbol{\nabla} \kappa_0 - \kappa_0\boldsymbol{M}_0\boldsymbol{\cdot} \boldsymbol{\nabla} \ln a_0 \right). \end{gather}$$
$$\begin{gather} \mathcal{L}_{0}\left(\hat \phi \right) = \boldsymbol{\nabla} \hat \phi \boldsymbol{\cdot} \left(-\boldsymbol{M}_0 \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{M}_0 + \boldsymbol{\nabla} \ln \rho_0 + \boldsymbol{M}_0( \boldsymbol{M}_0 \boldsymbol{\cdot} \boldsymbol{\nabla} \ln a_0) \right)\nonumber\\ +\, \mathrm{i} \hat \phi \left( \boldsymbol{M}_0\boldsymbol{\cdot} \boldsymbol{\nabla} \kappa_0 - \kappa_0\boldsymbol{M}_0\boldsymbol{\cdot} \boldsymbol{\nabla} \ln a_0 \right). \end{gather}$$Note that the sign of (2.9) has been reversed in (2.18), hence the definition of the source term in (2.16) as minus its right-hand side.
To set the context of the analysis, we now summarise the assumptions used up to this point. Viscous effects and, thus, the presence of boundary layers are neglected. Boundary layers are expected to enhance the shear of entropy waves close to the walls, especially in confined flows. Second, the magnitude of the entropic and acoustic waves is assumed to be small compared to the mean flow so that the governing equations can be linearised. The mean flow is assumed homentropic and irrotational. Finally, the mean flow is taken to be two-dimensional so that a streamfunction can be defined. This allows us to obtain the entropy distribution as in (2.12) and, thus, the source term given by (2.17).
3. Solution using the compact Green's function
In this section, we obtain an approximate solution to (2.18) using the Green's function method (Howe Reference Howe1975, Reference Howe2003). This equation has variable coefficients and further simplifications are required. In § 3.1, we simplify the acoustic propagation operator on the left-hand side using the Born approximation. An integral solution is then proposed in § 3.2.
3.1. Born approximation
Let us decompose the local Mach number and acoustic wavenumber on the left-hand side of (2.18) into an homogeneous and inhomogeneous part, such as
where ![]() $\boldsymbol {e}_{1}$ denotes the unit vector in the
$\boldsymbol {e}_{1}$ denotes the unit vector in the ![]() $x_1$-direction and
$x_1$-direction and ![]() $\kappa _{\infty }=\omega /a_{\infty }$ is the acoustic wavenumber in the far field. Equation (2.18) can now be recast as
$\kappa _{\infty }=\omega /a_{\infty }$ is the acoustic wavenumber in the far field. Equation (2.18) can now be recast as
 \begin{equation} \left[ \nabla^{2} + \left( \kappa_{\infty}+ \mathrm{i} M_{\infty}\frac{\partial}{\partial x_1}\right)^{2} \right]\hat \phi + \mathcal{L}_{\varDelta}\left( \hat \phi \right) = \hat S, \end{equation}
\begin{equation} \left[ \nabla^{2} + \left( \kappa_{\infty}+ \mathrm{i} M_{\infty}\frac{\partial}{\partial x_1}\right)^{2} \right]\hat \phi + \mathcal{L}_{\varDelta}\left( \hat \phi \right) = \hat S, \end{equation}
where the operator ![]() $\mathcal {L}_{\varDelta }$ is given by
$\mathcal {L}_{\varDelta }$ is given by
This operator captures the effect of the mean-flow inhomogeneity on the acoustic propagation. If its effect is weak, we can neglect it and assume that the source term acts on the uniform portion of the mean flow, such that
 \begin{equation} \left[ \nabla^{2} + \left( \kappa_{\infty} + \mathrm{i} M_{\infty}\frac{\partial}{\partial x_1}\right)^{2} \right]\hat \phi_{\infty} = \hat S. \end{equation}
\begin{equation} \left[ \nabla^{2} + \left( \kappa_{\infty} + \mathrm{i} M_{\infty}\frac{\partial}{\partial x_1}\right)^{2} \right]\hat \phi_{\infty} = \hat S. \end{equation}
This approximation can be further improved by considering the effect of the inhomogeneity on the acoustic field as a second-order source term correction, i.e. ![]() $\hat \phi = \hat \phi _{\infty } + \hat \phi _{\varDelta },$ where
$\hat \phi = \hat \phi _{\infty } + \hat \phi _{\varDelta },$ where ![]() $\hat \phi _{\varDelta }$ satisfies
$\hat \phi _{\varDelta }$ satisfies
 \begin{equation} \left[ \nabla^{2} + \left( \kappa_{\infty} + \mathrm{i} M_{\infty}\frac{\partial}{\partial x_1}\right)^{2} \right]\hat \phi_{\varDelta} ={-}\mathcal{L}_{\varDelta}\left( \hat \phi_{\infty} \right). \end{equation}
\begin{equation} \left[ \nabla^{2} + \left( \kappa_{\infty} + \mathrm{i} M_{\infty}\frac{\partial}{\partial x_1}\right)^{2} \right]\hat \phi_{\varDelta} ={-}\mathcal{L}_{\varDelta}\left( \hat \phi_{\infty} \right). \end{equation}The above is known as the first-order Born approximation (Snieder & Van Wijk Reference Snieder and Van Wijk2015, Ch. 23). Chew (Reference Chew1995, Ch. 8) established the regime of validity of the Born approximation for the Helmholtz equation, and showed that it was especially pertinent at low frequencies. In Appendix A, we use a similar approach to show that the Born approximation limits of validity for (3.2) are given by
 $$\begin{gather} He^{2} \; \delta \kappa ^{2} \ll 1, \quad He \; M_{\infty} \; \delta\kappa \; \delta M \ll 1,\quad M_{\infty}^{2} \; \delta M^{2} \ll 1, \quad He^{2} \; \delta \kappa \ll 1,\nonumber\\ He \; M_{\infty} \; \delta M \ll 1, \quad He \; M_{\infty} \; \delta \kappa \ll 1 \quad \text{and} \quad M_{\infty}^{2} \; \delta M \ll 1, \end{gather}$$
$$\begin{gather} He^{2} \; \delta \kappa ^{2} \ll 1, \quad He \; M_{\infty} \; \delta\kappa \; \delta M \ll 1,\quad M_{\infty}^{2} \; \delta M^{2} \ll 1, \quad He^{2} \; \delta \kappa \ll 1,\nonumber\\ He \; M_{\infty} \; \delta M \ll 1, \quad He \; M_{\infty} \; \delta \kappa \ll 1 \quad \text{and} \quad M_{\infty}^{2} \; \delta M \ll 1, \end{gather}$$
where ![]() $\delta \kappa$ and
$\delta \kappa$ and ![]() $\delta M$ represent the order of the normalised wavenumber and Mach number inhomogeneity, respectively, and
$\delta M$ represent the order of the normalised wavenumber and Mach number inhomogeneity, respectively, and ![]() $He=\omega b/a_{\infty }$ is the Helmholtz number. This shows that the Born approximation is perfectly suited to problems at low frequencies, low Mach numbers and with weak mean-flow inhomogeneities. In § 4, we simplify the source term by assuming that the mean flow is a small perturbation to a uniform flow. Equation (3.6a–g) shows that if this condition holds, the Born approximation is valid for any subsonic Mach number and for low-to-moderate frequencies. At high frequencies, the Born approximation is not suitable even for weak scatterers. This conclusion, which was obtained using simple dimensional analysis, was already postulated by Myers & Kerschen (Reference Myers and Kerschen1997) who showed the importance of accurately capturing the vortical-sound coupling between the leading and trailing edges to correctly predict the radiated far field at high frequencies. The present analysis also shows that this methodology can be used for aerofoils with larger thickness, camber or incoming angle of attack than those considered in the aforementioned studies, provided that the frequency and Mach number are sufficiently low.
$He=\omega b/a_{\infty }$ is the Helmholtz number. This shows that the Born approximation is perfectly suited to problems at low frequencies, low Mach numbers and with weak mean-flow inhomogeneities. In § 4, we simplify the source term by assuming that the mean flow is a small perturbation to a uniform flow. Equation (3.6a–g) shows that if this condition holds, the Born approximation is valid for any subsonic Mach number and for low-to-moderate frequencies. At high frequencies, the Born approximation is not suitable even for weak scatterers. This conclusion, which was obtained using simple dimensional analysis, was already postulated by Myers & Kerschen (Reference Myers and Kerschen1997) who showed the importance of accurately capturing the vortical-sound coupling between the leading and trailing edges to correctly predict the radiated far field at high frequencies. The present analysis also shows that this methodology can be used for aerofoils with larger thickness, camber or incoming angle of attack than those considered in the aforementioned studies, provided that the frequency and Mach number are sufficiently low.
To illustrate the solution method, we now consider the zeroth-order approximation, i.e. ![]() $\hat \phi =\hat \phi _{\infty }$. The first-order correction,
$\hat \phi =\hat \phi _{\infty }$. The first-order correction, ![]() $\hat \phi _{\varDelta }$, can be obtained equivalently by accordingly replacing the source term in the following procedure. A Lorentz-type transformation of the form:
$\hat \phi _{\varDelta }$, can be obtained equivalently by accordingly replacing the source term in the following procedure. A Lorentz-type transformation of the form:
 \begin{equation} \left. \begin{aligned} \tilde x_1 & = x_1/\beta_{\infty}, \quad \tilde x_2 = x_2, \quad \beta_{\infty} = \sqrt{1 - M_{\infty}^{2}},\\ \tilde \kappa_{\infty} & = \kappa_{\infty}/\beta_{\infty}, \quad \tilde \phi = \hat \phi \exp({\mathrm{i} \tilde \kappa_{\infty} {M_{\infty}} \tilde x_1}), \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} \tilde x_1 & = x_1/\beta_{\infty}, \quad \tilde x_2 = x_2, \quad \beta_{\infty} = \sqrt{1 - M_{\infty}^{2}},\\ \tilde \kappa_{\infty} & = \kappa_{\infty}/\beta_{\infty}, \quad \tilde \phi = \hat \phi \exp({\mathrm{i} \tilde \kappa_{\infty} {M_{\infty}} \tilde x_1}), \end{aligned} \right\} \end{equation}is now used to transform (3.4) into the Helmholtz equation, that is
Equation (3.8a,b) has been widely studied and can be solved using techniques available in the literature. Here, we propose a solution using the compact Green's function approach (Howe Reference Howe1975, Reference Howe2003) as outlined in § 3.2.
3.2. Integral solution using the compact Green's function method
Consider the Green's function ![]() $G(\tilde {\boldsymbol {x}},\tilde {\boldsymbol {y}})$ satisfying
$G(\tilde {\boldsymbol {x}},\tilde {\boldsymbol {y}})$ satisfying
where ![]() $\delta$ is the Dirac delta function. The physical meaning of this Green's function is the solution owing to a point source of unit strength at a point
$\delta$ is the Dirac delta function. The physical meaning of this Green's function is the solution owing to a point source of unit strength at a point ![]() $\tilde {\boldsymbol {y}},$ influenced by the surface
$\tilde {\boldsymbol {y}},$ influenced by the surface ![]() $\varSigma .$ In an unbounded fluid, this Green's function must also satisfy the radiation condition that energy delivered to the fluid by the source radiates away from the source, i.e. the solution must exhibit outgoing wave behaviour.
$\varSigma .$ In an unbounded fluid, this Green's function must also satisfy the radiation condition that energy delivered to the fluid by the source radiates away from the source, i.e. the solution must exhibit outgoing wave behaviour.
Consider the closed surface ![]() ${S}$ bounding the spatial domain
${S}$ bounding the spatial domain ![]() ${V}$, as depicted in figure 2. This surface comprises three subsurfaces:
${V}$, as depicted in figure 2. This surface comprises three subsurfaces: ![]() ${S} = \varSigma \cup {S}_{\infty } \cup {W},$ where
${S} = \varSigma \cup {S}_{\infty } \cup {W},$ where ![]() $\varSigma$ and
$\varSigma$ and ![]() ${W}$ are surfaces surrounding the aerofoil and the wake (the portion of the streamline that goes from the trailing edge to infinity downstream), respectively, and
${W}$ are surfaces surrounding the aerofoil and the wake (the portion of the streamline that goes from the trailing edge to infinity downstream), respectively, and ![]() ${S}_{\infty }$ is a surface very far from the aerofoil. We denote by
${S}_{\infty }$ is a surface very far from the aerofoil. We denote by ![]() $\boldsymbol {n}$ the inward unit normal to
$\boldsymbol {n}$ the inward unit normal to ![]() ${S}.$ Multiplying (3.8a,b) by the Green's function defined by (3.9a,b) and integrating over the domain
${S}.$ Multiplying (3.8a,b) by the Green's function defined by (3.9a,b) and integrating over the domain ![]() ${V},$ we obtain after some manipulations (see Appendix B) the following integral solution for the acoustic potential:
${V},$ we obtain after some manipulations (see Appendix B) the following integral solution for the acoustic potential:
 $$\begin{gather} \tilde \phi(\tilde{\boldsymbol{x}}) = \int_{{V}} G(\tilde{\boldsymbol{x}}, \tilde{\boldsymbol{y}})\tilde{S}(\,\tilde{\boldsymbol{y}})\,\textrm{d}{V}(\,\tilde{\boldsymbol{y}}) + \int_{\varSigma + {W}} G(\tilde{\boldsymbol{x}}, \tilde{\boldsymbol{y}}) \frac{\partial \hat \phi}{\partial \tilde{\boldsymbol{n}}}(\,\tilde{\boldsymbol{y}}) \exp({\mathrm{i} \tilde \kappa_{\infty} {M_{\infty}} \tilde y_1})\,\textrm{d}{S}(\,\tilde{\boldsymbol{y}})\nonumber\\ - \int_{{W}} \tilde \phi(\,\tilde{\boldsymbol{y}})\left( \frac{\partial G}{\partial \tilde{\boldsymbol{n}}}(\tilde{\boldsymbol{x}},\tilde{\boldsymbol{y}}) - \mathrm{i} \tilde{\kappa}_{\infty}{M_{\infty}} \tilde{n}_1 G(\tilde{\boldsymbol{x}},\tilde{\boldsymbol{y}})\right) \textrm{d}{S}(\,\tilde{\boldsymbol{y}}). \end{gather}$$
$$\begin{gather} \tilde \phi(\tilde{\boldsymbol{x}}) = \int_{{V}} G(\tilde{\boldsymbol{x}}, \tilde{\boldsymbol{y}})\tilde{S}(\,\tilde{\boldsymbol{y}})\,\textrm{d}{V}(\,\tilde{\boldsymbol{y}}) + \int_{\varSigma + {W}} G(\tilde{\boldsymbol{x}}, \tilde{\boldsymbol{y}}) \frac{\partial \hat \phi}{\partial \tilde{\boldsymbol{n}}}(\,\tilde{\boldsymbol{y}}) \exp({\mathrm{i} \tilde \kappa_{\infty} {M_{\infty}} \tilde y_1})\,\textrm{d}{S}(\,\tilde{\boldsymbol{y}})\nonumber\\ - \int_{{W}} \tilde \phi(\,\tilde{\boldsymbol{y}})\left( \frac{\partial G}{\partial \tilde{\boldsymbol{n}}}(\tilde{\boldsymbol{x}},\tilde{\boldsymbol{y}}) - \mathrm{i} \tilde{\kappa}_{\infty}{M_{\infty}} \tilde{n}_1 G(\tilde{\boldsymbol{x}},\tilde{\boldsymbol{y}})\right) \textrm{d}{S}(\,\tilde{\boldsymbol{y}}). \end{gather}$$
The integrals in ![]() ${S}_{\infty }$ vanish (see Wu & Lee Reference Wu and Lee1994). Along the wake, the source term can be singular, hence the acoustic potential can become discontinuous. The line integrals along the wake are retained to ensure the continuity of the pressure and normal velocity across it, as well as the Kutta condition at the trailing edge. In § 4, we show that in the thin-aerofoil limit this integral disappears. For simplicity's sake, we neglect it hereafter. The integral term over
${S}_{\infty }$ vanish (see Wu & Lee Reference Wu and Lee1994). Along the wake, the source term can be singular, hence the acoustic potential can become discontinuous. The line integrals along the wake are retained to ensure the continuity of the pressure and normal velocity across it, as well as the Kutta condition at the trailing edge. In § 4, we show that in the thin-aerofoil limit this integral disappears. For simplicity's sake, we neglect it hereafter. The integral term over ![]() $\varSigma$ represents the contribution to the acoustic field generated to satisfy the slip boundary condition on the body. For convenience, the surface
$\varSigma$ represents the contribution to the acoustic field generated to satisfy the slip boundary condition on the body. For convenience, the surface ![]() $\varSigma$ is further decomposed into two surfaces :
$\varSigma$ is further decomposed into two surfaces : ![]() $\varSigma = \varSigma ^{+} \cup \varSigma ^{-},$ where
$\varSigma = \varSigma ^{+} \cup \varSigma ^{-},$ where ![]() $\varSigma ^{+}$ and
$\varSigma ^{+}$ and ![]() $\varSigma ^{-}$ denote the upper and lower side of the aerofoil, respectively, going from the leading to the trailing edge.
$\varSigma ^{-}$ denote the upper and lower side of the aerofoil, respectively, going from the leading to the trailing edge.

Figure 2. Schematic of the region ![]() ${V}$ used in the derivation of the integral equation (3.10). Here,
${V}$ used in the derivation of the integral equation (3.10). Here, ![]() ${S}$ is the surface bounding
${S}$ is the surface bounding ![]() ${V}$:
${V}$: ![]() ${S} = \varSigma \cup {S}_{\infty } \cup {W}$.
${S} = \varSigma \cup {S}_{\infty } \cup {W}$.
An approximate solution to (3.9a,b) (to order ![]() $(\tilde \kappa _{\infty } b)^{2}$) is given by the compact Green's function approach of Howe (Reference Howe1975, Reference Howe2003) as
$(\tilde \kappa _{\infty } b)^{2}$) is given by the compact Green's function approach of Howe (Reference Howe1975, Reference Howe2003) as
for an observer at ![]() $\tilde {\boldsymbol {x}}$ and source at
$\tilde {\boldsymbol {x}}$ and source at ![]() $\tilde {\boldsymbol {y}}.$ Here,
$\tilde {\boldsymbol {y}}.$ Here, ![]() $\mathcal {H}_0^{(1)}$ and
$\mathcal {H}_0^{(1)}$ and ![]() $\mathcal {H}_1^{(1)}$ are the Hankel functions of the first kind for the zeroth and first order, respectively. The double index
$\mathcal {H}_1^{(1)}$ are the Hankel functions of the first kind for the zeroth and first order, respectively. The double index ![]() $j=1,2$ implies summation. The Kirchhoff vector
$j=1,2$ implies summation. The Kirchhoff vector ![]() $Y_j \equiv y_j - \varphi _j^{*}(\,\tilde {\boldsymbol {y}})$ satisfies
$Y_j \equiv y_j - \varphi _j^{*}(\,\tilde {\boldsymbol {y}})$ satisfies
subject to
The function ![]() $\varphi _j^{*}(\,\tilde {\boldsymbol {y}})$ represents the effect of the solid boundary on the acoustic response (see Howe Reference Howe2003 for a detailed description). Any acoustic source placed far from the aerofoil will be virtually not affected by it. To reflect this, we require that
$\varphi _j^{*}(\,\tilde {\boldsymbol {y}})$ represents the effect of the solid boundary on the acoustic response (see Howe Reference Howe2003 for a detailed description). Any acoustic source placed far from the aerofoil will be virtually not affected by it. To reflect this, we require that ![]() $\varphi _j^{*}(\,\tilde {\boldsymbol {y}})$ decays with distance from
$\varphi _j^{*}(\,\tilde {\boldsymbol {y}})$ decays with distance from ![]() $\varSigma .$
$\varSigma .$
The acoustic potential field is then obtained by substituting the compact Green's function given by (3.11) into (3.10) to yield:
 $$\begin{align} \tilde
\phi(\tilde{\boldsymbol{x}}) &= \frac{-\textrm{i}}{4} \left[
\mathcal{H}_0^{(1)}(\tilde
\kappa_{\infty}|\tilde{\boldsymbol{x}}|) \left(
\int_{V} \tilde S(\,\tilde{\boldsymbol{y}}) \;
\textrm{d}V(\,\tilde{\boldsymbol{y}}) + \int_{\varSigma}
\frac{\partial \hat \phi}{\partial
\tilde{\boldsymbol{n}}}(\,\tilde{\boldsymbol{y}})
\exp({\mathrm{i} \tilde \kappa_{\infty} {M_{\infty}} \tilde
y_1})\, \textrm{d} S(\,\tilde{\boldsymbol{y}})
\right)\right.\nonumber\\ &\quad + \left.\tilde \kappa_{\infty}
\frac{\tilde x_j }{|\tilde{\boldsymbol{x}}|}
\mathcal{H}_1^{(1)}(\tilde
\kappa_{\infty}|\tilde{\boldsymbol{x}}|) \left(
\int_{V} Y_j(\,\tilde{\boldsymbol{y}}) \tilde
S(\,\tilde{\boldsymbol{y}}) \; \textrm{d}V(\,\tilde{\boldsymbol{y}}) + \int_{\varSigma}
Y_j(\,\tilde{\boldsymbol{y}}) \frac{\partial \hat
\phi}{\partial
\tilde{\boldsymbol{n}}}(\,\tilde{\boldsymbol{y}})
\exp({\mathrm{i} \tilde \kappa_{\infty} {M_{\infty}} \tilde
y_1}) \, \textrm{d} S(\,\tilde{\boldsymbol{y}}) \right)
\right]. \end{align}$$
$$\begin{align} \tilde
\phi(\tilde{\boldsymbol{x}}) &= \frac{-\textrm{i}}{4} \left[
\mathcal{H}_0^{(1)}(\tilde
\kappa_{\infty}|\tilde{\boldsymbol{x}}|) \left(
\int_{V} \tilde S(\,\tilde{\boldsymbol{y}}) \;
\textrm{d}V(\,\tilde{\boldsymbol{y}}) + \int_{\varSigma}
\frac{\partial \hat \phi}{\partial
\tilde{\boldsymbol{n}}}(\,\tilde{\boldsymbol{y}})
\exp({\mathrm{i} \tilde \kappa_{\infty} {M_{\infty}} \tilde
y_1})\, \textrm{d} S(\,\tilde{\boldsymbol{y}})
\right)\right.\nonumber\\ &\quad + \left.\tilde \kappa_{\infty}
\frac{\tilde x_j }{|\tilde{\boldsymbol{x}}|}
\mathcal{H}_1^{(1)}(\tilde
\kappa_{\infty}|\tilde{\boldsymbol{x}}|) \left(
\int_{V} Y_j(\,\tilde{\boldsymbol{y}}) \tilde
S(\,\tilde{\boldsymbol{y}}) \; \textrm{d}V(\,\tilde{\boldsymbol{y}}) + \int_{\varSigma}
Y_j(\,\tilde{\boldsymbol{y}}) \frac{\partial \hat
\phi}{\partial
\tilde{\boldsymbol{n}}}(\,\tilde{\boldsymbol{y}})
\exp({\mathrm{i} \tilde \kappa_{\infty} {M_{\infty}} \tilde
y_1}) \, \textrm{d} S(\,\tilde{\boldsymbol{y}}) \right)
\right]. \end{align}$$
All the terms involving the observer position are moved outside of the integrals in (3.14) and, thus, the acoustic potential can be expressed as a linear combination of three basic components:
with
 \begin{gather}\alpha_j = \tilde \kappa_{\infty} \left( \int_{{V}} Y_j(\,\tilde{\boldsymbol{y}}) \tilde S(\,\tilde{\boldsymbol{y}}) \, \textrm{d} V(\,\tilde{\boldsymbol{y}}) + \int_{{\varSigma}} Y_j(\,\tilde{\boldsymbol{y}}) \frac{\partial \hat \phi}{\partial \tilde{\boldsymbol{n}}}(\,\tilde{\boldsymbol{y}}) \exp({\mathrm{i} \tilde \kappa_{\infty} {M_{\infty}} \tilde y_1}) \, \textrm{d} S(\,\tilde{\boldsymbol{y}}) \right), \end{gather}
\begin{gather}\alpha_j = \tilde \kappa_{\infty} \left( \int_{{V}} Y_j(\,\tilde{\boldsymbol{y}}) \tilde S(\,\tilde{\boldsymbol{y}}) \, \textrm{d} V(\,\tilde{\boldsymbol{y}}) + \int_{{\varSigma}} Y_j(\,\tilde{\boldsymbol{y}}) \frac{\partial \hat \phi}{\partial \tilde{\boldsymbol{n}}}(\,\tilde{\boldsymbol{y}}) \exp({\mathrm{i} \tilde \kappa_{\infty} {M_{\infty}} \tilde y_1}) \, \textrm{d} S(\,\tilde{\boldsymbol{y}}) \right), \end{gather}and
with ![]() $j = 1, 2.$
$j = 1, 2.$
Figure 3 shows these three components which are a monopole, a dipole in the horizontal axis and a dipole in the vertical axis. The velocity potential field, ![]() $\hat \phi (\boldsymbol {x}),$ will then depend on the geometry of the field through the weighting terms
$\hat \phi (\boldsymbol {x}),$ will then depend on the geometry of the field through the weighting terms ![]() $\alpha _0,$
$\alpha _0,$ ![]() $\alpha _1$ and
$\alpha _1$ and ![]() $\alpha _2$ in (3.15). The three components are affected by the Doppler factor
$\alpha _2$ in (3.15). The three components are affected by the Doppler factor ![]() $\exp ({-\mathrm {i} \tilde \kappa _{\infty }M_{\infty }\tilde x_1}),$ which causes the wavelength of the potential propagating in the forward direction to be shortened by the motion whereas the wavelength of the potential propagating in the rear direction is lengthened.
$\exp ({-\mathrm {i} \tilde \kappa _{\infty }M_{\infty }\tilde x_1}),$ which causes the wavelength of the potential propagating in the forward direction to be shortened by the motion whereas the wavelength of the potential propagating in the rear direction is lengthened.

Figure 3. Components of the solution of the acoustic potential, ![]() $\hat \phi ,$ for a flow
$\hat \phi ,$ for a flow ![]() $M_{\infty }=0.2$ and
$M_{\infty }=0.2$ and ![]() $He = 0.05:$ (a,d)
$He = 0.05:$ (a,d) ![]() $\phi _0;$ (b,e)
$\phi _0;$ (b,e) ![]() $\phi _1;$ and (c,f)
$\phi _1;$ and (c,f) ![]() $\phi _2.$ (a–c) Real part and (d–f) directivity.
$\phi _2.$ (a–c) Real part and (d–f) directivity.
The pressure field is then obtained from these three components using (2.7). If the observer is sufficiently far from the aerofoil, the mean flow velocity and density can be assumed uniform and the pressure field simplifies to
 \begin{equation} p'= \rho_{\infty}\left[ \mathrm{i} \omega \hat \phi - U_{\infty} \frac{\partial \hat \phi}{\partial x_1}\right], \end{equation}
\begin{equation} p'= \rho_{\infty}\left[ \mathrm{i} \omega \hat \phi - U_{\infty} \frac{\partial \hat \phi}{\partial x_1}\right], \end{equation}
which shows that the pressure field is given as a combination of the acoustic potential and its derivative in the streamwise direction ![]() $\partial {\hat \phi }/{\partial x_1}.$ The streamwise derivatives for the three potential components are given by
$\partial {\hat \phi }/{\partial x_1}.$ The streamwise derivatives for the three potential components are given by
 \begin{gather}\frac{\partial \phi_1}{\partial x_1} ={-}\frac{\kappa_{\infty}}{\beta_{\infty}^{2}}\left[ \mathrm{i} M_{\infty}\phi_1 - \frac{\mathrm{i}}{4}\left( \frac{\tilde x_1^{2}}{|\tilde{\boldsymbol{x}}|^{2}}\mathcal{H}_2^{(1)}(\tilde \kappa_{\infty}|\tilde{\boldsymbol{x}}|) - \frac{1}{|\tilde{\boldsymbol{x}}|}\frac{\mathcal{H}_1^{(1)}(\tilde \kappa_{\infty}|\tilde{\boldsymbol{x}}|)}{\tilde \kappa_{\infty}} \right) \exp({-\mathrm{i} \tilde \kappa_{\infty}M_{\infty}\tilde x_1}) \right], \end{gather}
\begin{gather}\frac{\partial \phi_1}{\partial x_1} ={-}\frac{\kappa_{\infty}}{\beta_{\infty}^{2}}\left[ \mathrm{i} M_{\infty}\phi_1 - \frac{\mathrm{i}}{4}\left( \frac{\tilde x_1^{2}}{|\tilde{\boldsymbol{x}}|^{2}}\mathcal{H}_2^{(1)}(\tilde \kappa_{\infty}|\tilde{\boldsymbol{x}}|) - \frac{1}{|\tilde{\boldsymbol{x}}|}\frac{\mathcal{H}_1^{(1)}(\tilde \kappa_{\infty}|\tilde{\boldsymbol{x}}|)}{\tilde \kappa_{\infty}} \right) \exp({-\mathrm{i} \tilde \kappa_{\infty}M_{\infty}\tilde x_1}) \right], \end{gather}
where ![]() $\mathcal {H}_2^{(1)}$ is the Hankel function of first kind and second order. These functions are depicted in figures 4 and 5 for two different Helmholtz numbers. The term
$\mathcal {H}_2^{(1)}$ is the Hankel function of first kind and second order. These functions are depicted in figures 4 and 5 for two different Helmholtz numbers. The term ![]() $\mathrm {i} M_{\infty }$ arises from the Doppler factor and causes the sound radiated in the forward direction to be amplified whereas the sound propagating in the rear direction is attenuated. For the first component, the monopole
$\mathrm {i} M_{\infty }$ arises from the Doppler factor and causes the sound radiated in the forward direction to be amplified whereas the sound propagating in the rear direction is attenuated. For the first component, the monopole ![]() $\phi _0,$ its derivative additionally includes a dipole whose wavelength and amplitude are accordingly modulated by the Doppler effect. For the second component, the dipole along the horizontal axis
$\phi _0,$ its derivative additionally includes a dipole whose wavelength and amplitude are accordingly modulated by the Doppler effect. For the second component, the dipole along the horizontal axis ![]() $\phi _1,$ its derivative additionally includes two terms: a flattened horizontal dipole and a term with a omnidirectional directivity, and that decays with distance and frequency faster than a monopole. Figure 4(b,e) and 5(b,e) show how at high frequencies the dominant contribution is the flattened dipole, while at lower frequencies both contributions are as important and combine to form a directivity pattern comprising four lobes along the two main axes. Finally, for the third component, the vertical dipole
$\phi _1,$ its derivative additionally includes two terms: a flattened horizontal dipole and a term with a omnidirectional directivity, and that decays with distance and frequency faster than a monopole. Figure 4(b,e) and 5(b,e) show how at high frequencies the dominant contribution is the flattened dipole, while at lower frequencies both contributions are as important and combine to form a directivity pattern comprising four lobes along the two main axes. Finally, for the third component, the vertical dipole ![]() $\phi _2,$ its derivative is a quadrupole also affected by the Doppler effect (stronger sound amplitude in the forward direction).
$\phi _2,$ its derivative is a quadrupole also affected by the Doppler effect (stronger sound amplitude in the forward direction).

Figure 4. Streamwise derivative of the components of the acoustic potential, ![]() $\partial {\hat \phi }/{\partial x_1},$ for a flow
$\partial {\hat \phi }/{\partial x_1},$ for a flow ![]() $M_{\infty }=0.2$ and
$M_{\infty }=0.2$ and ![]() $He = 0.05:$ (a,d)
$He = 0.05:$ (a,d) ![]() $\partial {\phi _0}/{\partial x_1};$ (b,e)
$\partial {\phi _0}/{\partial x_1};$ (b,e) ![]() $\partial {\phi _1}/{\partial x_1};$ and (c,f)
$\partial {\phi _1}/{\partial x_1};$ and (c,f) ![]() $\partial {\phi _2}/{\partial x_1}.$ (a–c) Real part and (d–f) directivity.
$\partial {\phi _2}/{\partial x_1}.$ (a–c) Real part and (d–f) directivity.
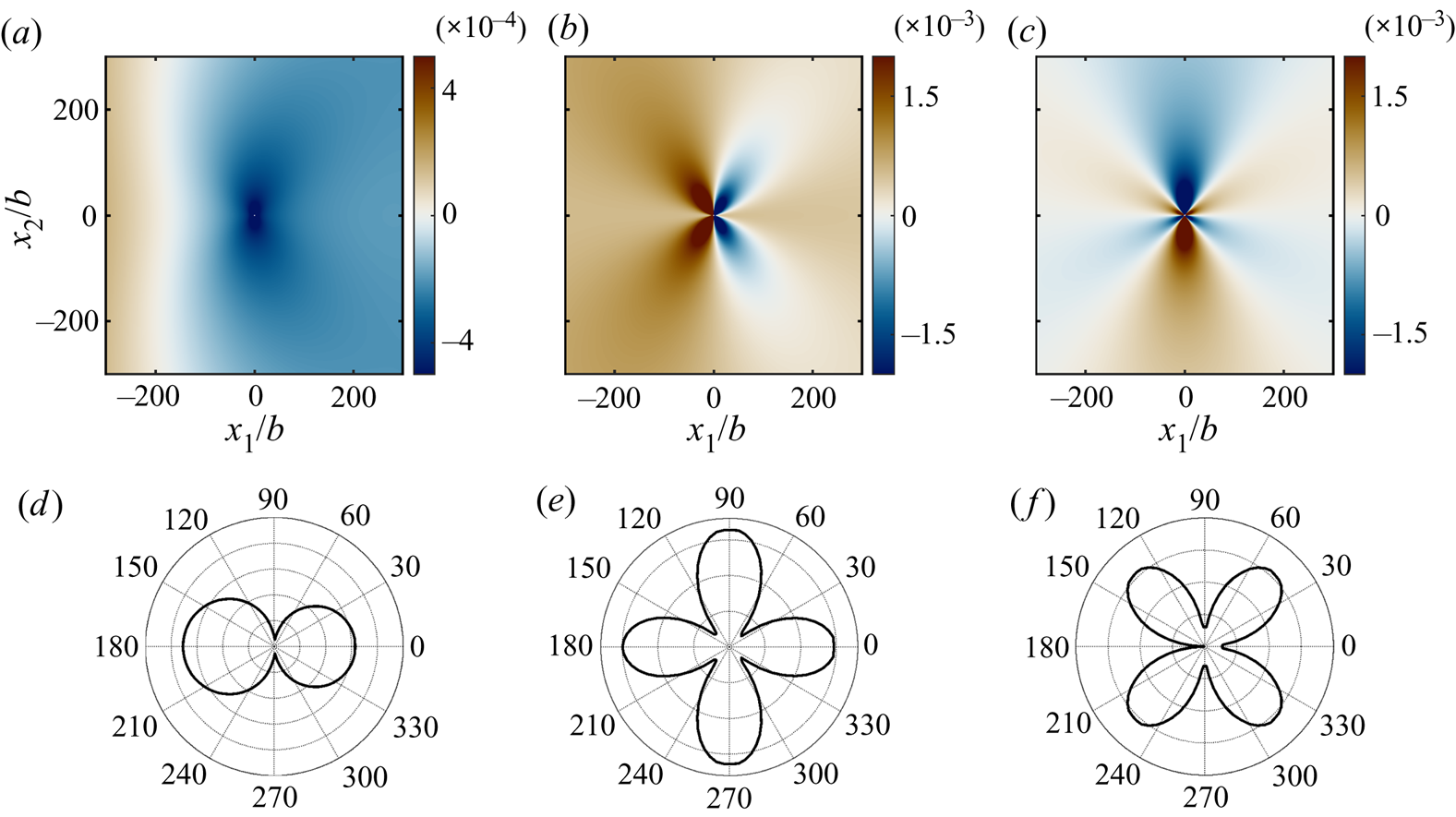
Figure 5. Streamwise derivative of the components of the acoustic potential, ![]() $\partial {\hat \phi }/{\partial x_1},$ for a flow
$\partial {\hat \phi }/{\partial x_1},$ for a flow ![]() $M_{\infty }=0.2$ and
$M_{\infty }=0.2$ and ![]() $He = 0.001:$ (a,d)
$He = 0.001:$ (a,d) ![]() $\partial {\phi _0}/{\partial x_1};$ (b,e)
$\partial {\phi _0}/{\partial x_1};$ (b,e) ![]() $\partial {\phi _1}/{\partial x_1};$ and (c,f)
$\partial {\phi _1}/{\partial x_1};$ and (c,f) ![]() $\partial {\phi _2}/{\partial x_1}.$ (a–c) Real part and (d–f) directivity.
$\partial {\phi _2}/{\partial x_1}.$ (a–c) Real part and (d–f) directivity.
The results presented up to this point constitute a contribution of the present work. The combination of the Born approximation with (2.9) allows the integral solution given by (3.10) to be obtained. This solution is valid within the limits summarised at the end of § 2 and those given by (3.6a–g). The solution expands the range of validity of analytical solutions beyond that available in the existing literature, because it allows aerofoils outside the scope of thin-aerofoil theory to be described. Finally, we restrict the analysis to low acoustic wavelengths (![]() $He^{2} \ll 1$) so that the computation of the Green's functions is greatly simplified and (3.14) is obtained. This expression can be readily integrated numerically provided that the details of the mean flow are available.
$He^{2} \ll 1$) so that the computation of the Green's functions is greatly simplified and (3.14) is obtained. This expression can be readily integrated numerically provided that the details of the mean flow are available.
4. Simplifications for thin aerofoils
To evaluate the source and boundary terms appearing in (3.14), the mean flow is required. This mean flow, given as the solution of the nonlinear compressible Euler equations, can be obtained either numerically or analytically. In the present work, we consider the latter so that explicit expressions for both the source and boundary terms are obtained. However, this requires further assumptions. Here, we restrict the aerofoil thickness, camber and angle of attack to be small, which allows one to assume that the mean flow is a small perturbation to a uniform flow (Ashley & Landahl Reference Ashley and Landahl1985; Kerschen & Myers Reference Kerschen and Myers1987), i.e.
where ![]() $q$ is the normalised perturbation in flow speed and
$q$ is the normalised perturbation in flow speed and ![]() $\epsilon$ is a small parameter so that
$\epsilon$ is a small parameter so that ![]() $\epsilon \ll 1.$ Neglecting terms of second order and above, the source term simplifies to
$\epsilon \ll 1.$ Neglecting terms of second order and above, the source term simplifies to
and the boundary condition on the aerofoil becomes
where ![]() $\varSigma ^{+}$ and
$\varSigma ^{+}$ and ![]() $\varSigma ^{-}$ denote the upper and lower side of the aerofoil, respectively. The function
$\varSigma ^{-}$ denote the upper and lower side of the aerofoil, respectively. The function ![]() $\beta _{\infty } \mu$ is the mean-flow angle relative to the uniform flow at upstream infinity.
$\beta _{\infty } \mu$ is the mean-flow angle relative to the uniform flow at upstream infinity.
The computation of the mean-flow variables is also substantially simplified by the use of thin-aerofoil theory. The mean-flow potential ![]() $\varPhi$ can be linearised as
$\varPhi$ can be linearised as
where the perturbation potential ![]() $\varPhi _1$ satisfies
$\varPhi _1$ satisfies
and appropriate conditions on the body surface. Using the Prandtl–Glauert transformation:
this equation becomes the Laplace equation (Ashley & Landahl Reference Ashley and Landahl1985). This transformation effectively recasts the compressible mean flow problem as an equivalent incompressible flow in a scaled domain. The compressible perturbation velocity potential and stream function ![]() $F(z) = \varPhi _1 + \mathrm {i} \varPsi _1$ are related to the incompressible complex potential
$F(z) = \varPhi _1 + \mathrm {i} \varPsi _1$ are related to the incompressible complex potential ![]() $\bar {F}(z)$ by
$\bar {F}(z)$ by
where ![]() $z = \bar {x}_1 + \mathrm {i}\bar {x}_2$ contains the coordinates of the incompressible domain. The potential and stream functions can also be written as a complex function
$z = \bar {x}_1 + \mathrm {i}\bar {x}_2$ contains the coordinates of the incompressible domain. The potential and stream functions can also be written as a complex function ![]() $\zeta = \varPhi + \mathrm {i} \varPsi ,$ which allows us to write
$\zeta = \varPhi + \mathrm {i} \varPsi ,$ which allows us to write
The perturbation velocity ![]() $(\mathcal{V}= q - \mathrm {i}\mu )$ and acceleration along a streamline are given, respectively, by
$(\mathcal{V}= q - \mathrm {i}\mu )$ and acceleration along a streamline are given, respectively, by
The drift function (2.14) simplifies to
and using (4.9a,b) becomes
To simplify the following calculations the integrals in (3.16) are split as follows:
with
and ![]() $j = 1, 2.$ The volume integrals have been transformed to the equivalent incompressible domain, with the factor
$j = 1, 2.$ The volume integrals have been transformed to the equivalent incompressible domain, with the factor ![]() $1/\beta _{\infty }^{2}$ being the Jacobian of the change of variables. The term
$1/\beta _{\infty }^{2}$ being the Jacobian of the change of variables. The term ![]() $\sigma =\boldsymbol {k}\boldsymbol {\cdot } \boldsymbol {X}+\tilde \kappa _{\infty } {M_{\infty }} \tilde x_1$ in the exponentials can be simplified as
$\sigma =\boldsymbol {k}\boldsymbol {\cdot } \boldsymbol {X}+\tilde \kappa _{\infty } {M_{\infty }} \tilde x_1$ in the exponentials can be simplified as
where ![]() $St= \omega b/U_{\infty }$ is the Strouhal number based on the semi-chord of the aerofoil.
$St= \omega b/U_{\infty }$ is the Strouhal number based on the semi-chord of the aerofoil.
The thin-aerofoil approximation also leads to the first-order correction of the Born approximation (3.5) being negligible. The zero-order term is ![]() $\hat \phi _{\infty }=O(\epsilon )$ because the source term and boundary condition are of that order. Additionally, the operator
$\hat \phi _{\infty }=O(\epsilon )$ because the source term and boundary condition are of that order. Additionally, the operator ![]() $\mathcal {L}_{\varDelta }$ becomes
$\mathcal {L}_{\varDelta }$ becomes ![]() $\textit {O}(\epsilon ).$ The source term is
$\textit {O}(\epsilon ).$ The source term is ![]() $\mathcal {L}_{\varDelta }(\hat \phi _{\infty })=\textit {O}(\epsilon ^{2}),$ hence the potential is
$\mathcal {L}_{\varDelta }(\hat \phi _{\infty })=\textit {O}(\epsilon ^{2}),$ hence the potential is ![]() $\hat \phi _{\varDelta }=O(\epsilon ^{2})$ and can be neglected.
$\hat \phi _{\varDelta }=O(\epsilon ^{2})$ and can be neglected.
Finally, the thin-aerofoil limit also allows the third integral in (3.10) to be neglected. This integral appears because the source term given by (2.16) is singular along the streamline going through the aerofoil (which contains the aerofoil and the wake) which means that the acoustic potential can become discontinuous across it. This integral is used to enforce continuity of pressure across the wake. Because the singularity is moved to higher-order terms, the continuity of both the potential and pressure field is guaranteed up to this order.
5. Sound generated by thin symmetric aerofoils
In this section, we particularise the theory previously outlined to a thin, symmetric aerofoil. Specifically, we consider a canonical Joukowsky profile whose mean flow can be obtained analytically using conformal mapping. Such an aerofoil is parametrised by
with ![]() $\theta \in [ 0, 2{\rm \pi} ),$
$\theta \in [ 0, 2{\rm \pi} ),$ ![]() $\tau _0=-\epsilon /(1+\epsilon )$ and
$\tau _0=-\epsilon /(1+\epsilon )$ and ![]() $a = 1/(\epsilon + 1).$ Here, the expansion parameter
$a = 1/(\epsilon + 1).$ Here, the expansion parameter ![]() $\epsilon$ corresponds to approximately half the maximum thickness of the aerofoil (normalised by its semi-chord). All the results are obtained for a case defined by
$\epsilon$ corresponds to approximately half the maximum thickness of the aerofoil (normalised by its semi-chord). All the results are obtained for a case defined by ![]() $\epsilon =0.05.$
$\epsilon =0.05.$
5.1. Numerical results
We first compute a numerical solution of the two-dimensional compressible Euler equations as a benchmark for the model. Both the steady and linearised Euler equations are solved using the finite element method (Donea & Huerta Reference Donea and Huerta2003) implemented using the open-source computing platform FEniCS (Logg et al. Reference Logg2012; Alnæs et al. Reference Alnæs, Blechta, Hake, Johansson, Kehlet, Logg, Richardson, Ring, Rognes and Wells2015).
The mean flow is obtained as the solution of the steady compressible Euler equations in conservation variables. The equations are discretised in space using a continuous Galerkin formulation stabilised using the least-squares method (Donea & Huerta Reference Donea and Huerta2003). The discretised nonlinear problem is solved using a fully-implicit, pseudo-time-stepping algorithm (Crivellini, D'Alessandro & Bassi Reference Crivellini, D'Alessandro and Bassi2013). The algorithm adapts the local time step every iteration so that it is inversely proportional to the local residuals. When the residuals are small, the time step becomes large, the unsteady term negligible and the algorithm effectively behaves as the Newton method, exhibiting quadratic convergence. The global residuals (in norm-2) for all the results presented hereafter are lower than ![]() $10^{-9}.$ The results are typically obtained in less than 100 iterations. At the aerofoil boundary we require the fluid to satisfy the slip boundary condition. At the inlet we impose uniform velocity and density, and at the outlet we impose uniform pressure. The meshes used in this study are fully unstructured and contain approximately 200 000 triangular elements. The approximation polynomials are quadratic. The domain is a square with the length of a side being
$10^{-9}.$ The results are typically obtained in less than 100 iterations. At the aerofoil boundary we require the fluid to satisfy the slip boundary condition. At the inlet we impose uniform velocity and density, and at the outlet we impose uniform pressure. The meshes used in this study are fully unstructured and contain approximately 200 000 triangular elements. The approximation polynomials are quadratic. The domain is a square with the length of a side being ![]() $26b.$
$26b.$
Figure 6 depicts the mean flow obtained numerically. At the leading edge of the aerofoil, the flow quickly decelerates from the upstream velocity to being stagnant. It then accelerates until the point of maximum thickness of the aerofoil and gently decelerates thereafter until the trailing edge. Note that for Joukowsky aerofoils, a second stagnation point does not exist there (in contrast with realistic aerofoils). At the point of largest velocity, its increase never exceeds ![]() $20\,\%$ of the unperturbed velocity. Therefore, the main acceleration occurs in the region around the stagnation point at the leading edge. This velocity variation translates to the density and speed of sound. The speed of sound does not exceed
$20\,\%$ of the unperturbed velocity. Therefore, the main acceleration occurs in the region around the stagnation point at the leading edge. This velocity variation translates to the density and speed of sound. The speed of sound does not exceed ![]() $2\,\%$ of the unperturbed one in any case. The variation of density is larger, reaching variations of
$2\,\%$ of the unperturbed one in any case. The variation of density is larger, reaching variations of ![]() $4\,\%$ at the leading edge for
$4\,\%$ at the leading edge for ![]() $M_{\infty }=0.5,$ but remains low enough to neglect them in the analytical model.
$M_{\infty }=0.5,$ but remains low enough to neglect them in the analytical model.

Figure 6. Normalised density ![]() $\rho _0/\rho _{\infty },$ local Mach number
$\rho _0/\rho _{\infty },$ local Mach number ![]() $M_0=U_0/a_0$ and normalised speed of sound
$M_0=U_0/a_0$ and normalised speed of sound ![]() $a_0/a_{\infty }$ for a symmetric aerofoil at (a–c)
$a_0/a_{\infty }$ for a symmetric aerofoil at (a–c) ![]() ${M_{\infty }}=0.2$ and (d–f)
${M_{\infty }}=0.2$ and (d–f) ![]() ${M_{\infty }}=0.5.$
${M_{\infty }}=0.5.$
We now turn our attention to the acoustic problem. The linearised compressible Euler equations are formulated in primitive variables and recast in the frequency domain. Then, they are spatially discretised using the discontinuous Galerkin method (Bassi & Rebay Reference Bassi and Rebay1997; Cockburn & Shu Reference Cockburn and Shu2001). The discretisation leads to a linear problem that is solved using the sparse linear solver MUMPS (Amestoy et al. Reference Amestoy, Duff, Koster and L'Excellent2001, Reference Amestoy, Guermouche, L'Excellent and Pralet2006). A perfectly matched layer (PML) (Hu Reference Hu2001) was added to the domain to damp any incoming acoustic wave. To enforce the incoming entropy waves, an incident density fluctuation was superimposed to the reflected solution in the PML (Özyörük Reference Özyörük2009). A slip boundary condition is used on the aerofoil.
The current implementation of the finite element method allows for approximation polynomials whose order range ![]() $p=0 - 5.$ The bulk of the simulations are carried out using quadratic elements
$p=0 - 5.$ The bulk of the simulations are carried out using quadratic elements ![]() $p=2$. However, to assess the accuracy of the results, simulations with cubic elements were performed for the highest frequencies showing the independence of the results to the order of the polynomials. Additionally, a mesh convergence study was performed showing that 20 points per entropy wavelength are sufficient to obtain mesh-independent results. The final mesh used for the study is unstructured and is composed approximately of 150 000 triangular elements. The domain is again a square. The length of the domain is varied from
$p=2$. However, to assess the accuracy of the results, simulations with cubic elements were performed for the highest frequencies showing the independence of the results to the order of the polynomials. Additionally, a mesh convergence study was performed showing that 20 points per entropy wavelength are sufficient to obtain mesh-independent results. The final mesh used for the study is unstructured and is composed approximately of 150 000 triangular elements. The domain is again a square. The length of the domain is varied from ![]() $20b$ to
$20b$ to ![]() $40b.$ All the domains are extended by a PML of length
$40b.$ All the domains are extended by a PML of length ![]() $5b.$ The PML coefficients are
$5b.$ The PML coefficients are ![]() $\sigma _m=6$ and
$\sigma _m=6$ and ![]() $\beta =2$ (as defined by Hu Reference Hu2001). For the highest frequencies considered here, the simulations are independent of the size of the domain. However, for the lowest frequency (corresponding to
$\beta =2$ (as defined by Hu Reference Hu2001). For the highest frequencies considered here, the simulations are independent of the size of the domain. However, for the lowest frequency (corresponding to ![]() $He=0.001$), small variations are observed for different domains. This indicates that the simulation for this frequency is not fully converged in domain size (larger domains are beyond our current computational capabilities). The variations of the acoustic directivity with different sizes are small enough to assure that the results will not change dramatically for larger domains. Note that the effect of the PML layer was ruled out by running several simulations with different sets of PML parameters for every domain size. Figure 7 shows an example of the acoustic field obtained from the simulations, which shows that for a plane entropy wave the generated acoustic field resembles a dipole radiating along the horizontal axis.
$He=0.001$), small variations are observed for different domains. This indicates that the simulation for this frequency is not fully converged in domain size (larger domains are beyond our current computational capabilities). The variations of the acoustic directivity with different sizes are small enough to assure that the results will not change dramatically for larger domains. Note that the effect of the PML layer was ruled out by running several simulations with different sets of PML parameters for every domain size. Figure 7 shows an example of the acoustic field obtained from the simulations, which shows that for a plane entropy wave the generated acoustic field resembles a dipole radiating along the horizontal axis.

Figure 7. Numerical results: real parts of the (a) perturbation density, ![]() $\rho '/\rho _{\infty },$ and (b) pressure,
$\rho '/\rho _{\infty },$ and (b) pressure, ![]() $p'/\gamma p_{\infty },$ for a symmetric aerofoil at
$p'/\gamma p_{\infty },$ for a symmetric aerofoil at ![]() ${M_{\infty }}=0.2$ and
${M_{\infty }}=0.2$ and ![]() $He=0.5$.
$He=0.5$.
5.2. Source term and Kirchhoff vectors
The incompressible mean-flow potential is obtained by mapping a cylinder of unit radius centred at the origin (![]() $\tau$-plane) into the aerofoil defined by (5.1a,b) (
$\tau$-plane) into the aerofoil defined by (5.1a,b) (![]() $z$-plane) as follows:
$z$-plane) as follows:
The incompressible potential in the ![]() $\tau$-plane is given by
$\tau$-plane is given by
The incompressible perturbation potential ![]() $(\epsilon \bar {F}=f/U_{\infty }-z)$ is obtained as
$(\epsilon \bar {F}=f/U_{\infty }-z)$ is obtained as
The perturbation velocity is
Figure 8 compares the normalised mean-flow pressure coefficient obtained using the numerical simulations with the predictions of linearised theory. Note that the compressible variables are obtained from the incompressible ones through the Prandtl–Glauert transformation (see §§ 2.1 and 4). At low Mach numbers, the analytical results closely match the simulations over the entire blade. For ![]() ${M_{\infty }}=0.5,$ the agreement is still good for most of the aerofoil, but some discrepancies appear close to the leading edge. This is because thin-aerofoil theory breaks down at that point. For
${M_{\infty }}=0.5,$ the agreement is still good for most of the aerofoil, but some discrepancies appear close to the leading edge. This is because thin-aerofoil theory breaks down at that point. For ![]() ${M_{\infty }}=0.7,$ some mismatch between simulations and theory are noticeable over the whole surface and are more pronounced at the leading edge. Overall, the results suggest that potential theory is a good approximation for this problem.
${M_{\infty }}=0.7,$ some mismatch between simulations and theory are noticeable over the whole surface and are more pronounced at the leading edge. Overall, the results suggest that potential theory is a good approximation for this problem.

Figure 8. Mean-flow surface pressure coefficient for different Mach numbers obtained numerically (blue dashed) and using potential theory (black solid).
The velocity and acceleration components involved in the calculation of the source term of (4.2) are shown in figure 9. It is apparent that the region that contributes most to the noise generation is the area around the leading edge. Both the perturbation velocity ![]() $q$ and its acceleration
$q$ and its acceleration ![]() $\partial q/\partial \varPhi$ exhibit reflectional symmetry with respect to the horizontal axis
$\partial q/\partial \varPhi$ exhibit reflectional symmetry with respect to the horizontal axis ![]() $(x_2=0)$ whereas the perturbation to the mean-flow angle
$(x_2=0)$ whereas the perturbation to the mean-flow angle ![]() $\mu$ is antisymmetric. These considerations have important implications when integrating the source term.
$\mu$ is antisymmetric. These considerations have important implications when integrating the source term.

Figure 9. Components of the source term (4.2).
The last necessary elements for the model are the Kirchhoff vectors ![]() $Y_j= y_j - \varphi ^{*}(\kern0.5pt y_j).$ To obtain an analytical expression for them, we restrict the analysis to flows satisfying
$Y_j= y_j - \varphi ^{*}(\kern0.5pt y_j).$ To obtain an analytical expression for them, we restrict the analysis to flows satisfying ![]() $\tilde \kappa _{\infty } M_{\infty } \ll 1,$ so that the second term in (3.13) disappears. The problem then simplifies to solving a Laplace equation with slip boundary conditions on the aerofoil and conformal mapping can be used again to obtain
$\tilde \kappa _{\infty } M_{\infty } \ll 1,$ so that the second term in (3.13) disappears. The problem then simplifies to solving a Laplace equation with slip boundary conditions on the aerofoil and conformal mapping can be used again to obtain
Note that when the term ![]() $\epsilon =0,$ the expressions correspond to the Kirchhoff vectors for a flat plate. When we multiply the source term (
$\epsilon =0,$ the expressions correspond to the Kirchhoff vectors for a flat plate. When we multiply the source term (![]() ${O}(\epsilon$)) by the Kirchhoff vectors, the second terms in both the Kirchhoff vectors become
${O}(\epsilon$)) by the Kirchhoff vectors, the second terms in both the Kirchhoff vectors become ![]() ${O}(\epsilon ^{2})$ and can be neglected. This means that, in the limit
${O}(\epsilon ^{2})$ and can be neglected. This means that, in the limit ![]() $\epsilon \ll 1$, the aerofoil can be approximated as a flat plate. In other words, the effect that the solid boundaries of the blade have in the acoustic response is equivalent to that of a flat plate.
$\epsilon \ll 1$, the aerofoil can be approximated as a flat plate. In other words, the effect that the solid boundaries of the blade have in the acoustic response is equivalent to that of a flat plate.
Figure 10 shows the Kirchhoff vectors ![]() $Y_1$ and
$Y_1$ and ![]() $Y_2$ that are symmetric and antisymmetric with respect to the horizontal axis, respectively. This has consequences when evaluating the acoustic integrals: any source term with horizontal symmetry will contribute to the integrals in
$Y_2$ that are symmetric and antisymmetric with respect to the horizontal axis, respectively. This has consequences when evaluating the acoustic integrals: any source term with horizontal symmetry will contribute to the integrals in ![]() $\alpha _0$ and
$\alpha _0$ and ![]() $\alpha _1$ that weight a monopole and a horizontal dipole, respectively. Using symmetry considerations, the integrals in
$\alpha _1$ that weight a monopole and a horizontal dipole, respectively. Using symmetry considerations, the integrals in ![]() $\alpha _2$ vanish and, thus, a symmetric source does not contribute to the vertical dipole solution. For an antisymmetric source, the conclusion is the inverse: the terms
$\alpha _2$ vanish and, thus, a symmetric source does not contribute to the vertical dipole solution. For an antisymmetric source, the conclusion is the inverse: the terms ![]() $\alpha _0$ and
$\alpha _0$ and ![]() $\alpha _1$ are cancelled and the source only contributes to the potential as a dipole along the vertical axis.
$\alpha _1$ are cancelled and the source only contributes to the potential as a dipole along the vertical axis.

Figure 10. Kirchhoff vectors ![]() $Y_j= y_j - \varphi _j^{*}(\,\boldsymbol {y}).$ The functions
$Y_j= y_j - \varphi _j^{*}(\,\boldsymbol {y}).$ The functions ![]() $\varphi _j^{*}$ capture the influence of the aerofoil on the acoustic field.
$\varphi _j^{*}$ capture the influence of the aerofoil on the acoustic field.
Figure 10 also depicts the functions ![]() $\varphi ^{*}_j(\kern0.5pt y_j)$ that represent the influence of the solid boundary on the acoustic potential. The physical meaning of these functions can be intuitively understood if a point source is considered. This source can be placed, for instance, on the horizontal axis close to the leading edge. The resulting acoustic potential is the sum of a monopole, as in free-space, together with a horizontal dipole owing to the shielding of the aerofoil. This is apparent from
$\varphi ^{*}_j(\kern0.5pt y_j)$ that represent the influence of the solid boundary on the acoustic potential. The physical meaning of these functions can be intuitively understood if a point source is considered. This source can be placed, for instance, on the horizontal axis close to the leading edge. The resulting acoustic potential is the sum of a monopole, as in free-space, together with a horizontal dipole owing to the shielding of the aerofoil. This is apparent from ![]() $\varphi ^{*}_j: \varphi ^{*}_1$ is relatively large at that point whereas
$\varphi ^{*}_j: \varphi ^{*}_1$ is relatively large at that point whereas ![]() $\varphi ^{*}_2$ is close to zero. If the point source is now placed on the upper side of the aerofoil, close to the point of maximum thickness, the acoustic potential is given by the combination of a monopole and a vertical dipole (which arises again from the shielding of the blade). This is captured by
$\varphi ^{*}_2$ is close to zero. If the point source is now placed on the upper side of the aerofoil, close to the point of maximum thickness, the acoustic potential is given by the combination of a monopole and a vertical dipole (which arises again from the shielding of the blade). This is captured by ![]() $\varphi ^{*}_2$ being large at that point and
$\varphi ^{*}_2$ being large at that point and ![]() $\varphi ^{*}_1$ being negligible.
$\varphi ^{*}_1$ being negligible.
5.3. Acoustic response
We now compute the integrals in (4.14) to obtain a closed form of the perturbation pressure ![]() $p'$. To evaluate the integrals, these are transformed to the cylindrical domain (
$p'$. To evaluate the integrals, these are transformed to the cylindrical domain (![]() $\tau$-plane) and then expressed in cylindrical coordinates. An example is given below:
$\tau$-plane) and then expressed in cylindrical coordinates. An example is given below:
 $$\begin{align} \textrm{I}^{(0)}_q
&=\frac{1}{\beta_{\infty}^{3}} \int_{{V}} \mathrm{Re}
\left\{ \frac{\textrm{d}\bar{F}}{\textrm{d}z} \right\}
\frac{\textrm{d}z}{\textrm{d}\tau}\overline{\frac{\textrm{d}z}{\textrm{d}\tau}}
\,\textrm{e}^{\mathrm{i} \sigma} \,
\textrm{d}{\tau_1}\textrm{d}{\tau_2} \nonumber\\ &=
\frac{1}{\beta_{\infty}^{3}} \int_{1}^{\infty} \int_0^{2
{\rm \pi}} \left[ r \mathrm{Re} \left\{
\frac{\textrm{d}\bar{F}}{\textrm{d}\tau}
\overline{\frac{\textrm{d}z}{\textrm{d}\tau}}\right\}
\,\textrm{e}^{\mathrm{i} \sigma} \right] \,
\textrm{d}{\theta}\,\textrm{d}{r}.
\end{align}$$
$$\begin{align} \textrm{I}^{(0)}_q
&=\frac{1}{\beta_{\infty}^{3}} \int_{{V}} \mathrm{Re}
\left\{ \frac{\textrm{d}\bar{F}}{\textrm{d}z} \right\}
\frac{\textrm{d}z}{\textrm{d}\tau}\overline{\frac{\textrm{d}z}{\textrm{d}\tau}}
\,\textrm{e}^{\mathrm{i} \sigma} \,
\textrm{d}{\tau_1}\textrm{d}{\tau_2} \nonumber\\ &=
\frac{1}{\beta_{\infty}^{3}} \int_{1}^{\infty} \int_0^{2
{\rm \pi}} \left[ r \mathrm{Re} \left\{
\frac{\textrm{d}\bar{F}}{\textrm{d}\tau}
\overline{\frac{\textrm{d}z}{\textrm{d}\tau}}\right\}
\,\textrm{e}^{\mathrm{i} \sigma} \right] \,
\textrm{d}{\theta}\,\textrm{d}{r}.
\end{align}$$
Note that the term ![]() $({\textrm {d}z}/{\textrm {d}\tau })(\overline {{\textrm {d}z}/{\textrm {d}\tau }})$ corresponds to the Jacobian of the transformation from the z-plane to the
$({\textrm {d}z}/{\textrm {d}\tau })(\overline {{\textrm {d}z}/{\textrm {d}\tau }})$ corresponds to the Jacobian of the transformation from the z-plane to the ![]() $\tau$-plane. The source terms and Kirchhoff vectors in the integrand are expressed as a sum of rational terms. However, to the best of the authors’ knowledge, the integrals preclude an analytical solution owing to the exponential term
$\tau$-plane. The source terms and Kirchhoff vectors in the integrand are expressed as a sum of rational terms. However, to the best of the authors’ knowledge, the integrals preclude an analytical solution owing to the exponential term ![]() $\textrm {e}^{\mathrm {i} \sigma }$ and must be obtained numerically. To approximate the integrals, we truncate the infinite limit in the radius to a finite number. The convergence with respect to this value is assessed in Appendix C.
$\textrm {e}^{\mathrm {i} \sigma }$ and must be obtained numerically. To approximate the integrals, we truncate the infinite limit in the radius to a finite number. The convergence with respect to this value is assessed in Appendix C.
The numerical values obtained for the integrals are depicted in figure 11. The ![]() $\beta _{\infty }$-factor is removed from the integrals as
$\beta _{\infty }$-factor is removed from the integrals as
 \begin{equation} \left. \begin{aligned} \textrm{I}^{(0)}_q & = \textrm{I}^{(0)*}_q \left(b^{2}/\beta_{\infty}^{3}\right), \quad \textrm{I}^{(0)}_{\partial q} = \textrm{I}^{(0)*}_{\partial q}\left(b\phantom{{}^{2}}/\beta_{\infty}^{3}\right), \quad \textrm{J}^{(0)}_{\mu} = \textrm{J}^{(0)*}_{\mu}\left(b\phantom{{}^{2}}/\beta_{\infty}^{2}\right), \\ \textrm{I}^{(1)}_q & = \textrm{I}^{(1)*}_q\left(b^{3}/\beta_{\infty}^{4}\right), \quad \textrm{I}^{(1)}_{\partial q} = \textrm{I}^{(1)*}_{\partial q}\left(b^{2}/\beta_{\infty}^{4}\right), \quad \textrm{J}^{(1)}_{\mu} = \textrm{J}^{(1)*}_{\mu}\left(b^{2}/\beta_{\infty}^{3}\right), \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} \textrm{I}^{(0)}_q & = \textrm{I}^{(0)*}_q \left(b^{2}/\beta_{\infty}^{3}\right), \quad \textrm{I}^{(0)}_{\partial q} = \textrm{I}^{(0)*}_{\partial q}\left(b\phantom{{}^{2}}/\beta_{\infty}^{3}\right), \quad \textrm{J}^{(0)}_{\mu} = \textrm{J}^{(0)*}_{\mu}\left(b\phantom{{}^{2}}/\beta_{\infty}^{2}\right), \\ \textrm{I}^{(1)}_q & = \textrm{I}^{(1)*}_q\left(b^{3}/\beta_{\infty}^{4}\right), \quad \textrm{I}^{(1)}_{\partial q} = \textrm{I}^{(1)*}_{\partial q}\left(b^{2}/\beta_{\infty}^{4}\right), \quad \textrm{J}^{(1)}_{\mu} = \textrm{J}^{(1)*}_{\mu}\left(b^{2}/\beta_{\infty}^{3}\right), \end{aligned} \right\} \end{equation}
so that they can be expressed only as functions of ![]() $St^{*}=St/\beta _{\infty }^{2}.$ For
$St^{*}=St/\beta _{\infty }^{2}.$ For ![]() $St^{*} < 0.5,$ clear trends arise from the results, which can be summarised as follows:
$St^{*} < 0.5,$ clear trends arise from the results, which can be summarised as follows:
 \begin{equation} \left. \begin{aligned} \textrm{I}^{(0)*}_q & \simeq {\rm \pi}- \mathrm{i} \frac{\rm \pi}{4} St^{*}, \quad \textrm{I}^{(1)*}_q \simeq{-}\frac{\rm \pi}{4} + \mathrm{i} \frac{\rm \pi}{4} St^{*}, \quad \textrm{I}^{(2)}_q\simeq 0,\\ \textrm{I}^{(0)*}_{\partial q} & \simeq{-}\frac{\rm \pi}{4} St^{*2} - \mathrm{i} {\rm \pi}St^{*} , \quad \textrm{I}^{(1)*}_{\partial q} \simeq{-}{\rm \pi} + \mathrm{i}\frac{\rm \pi}{2}St^{*}, \quad\textrm{I}^{(2)}_{\partial q} \simeq 0,\\ \textrm{J}^{(0)*}_{\mu} & \simeq{-}\frac{\rm \pi}{4} St^{*2}-\mathrm{i}{\rm \pi} St^{*} , \quad \textrm{J}^{(1)*}_{\mu} \simeq{-}{\rm \pi} + \mathrm{i}\frac{\rm \pi}{2} St^{*}, \quad \textrm{J}^{(2)}_{\mu} \simeq 0. \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} \textrm{I}^{(0)*}_q & \simeq {\rm \pi}- \mathrm{i} \frac{\rm \pi}{4} St^{*}, \quad \textrm{I}^{(1)*}_q \simeq{-}\frac{\rm \pi}{4} + \mathrm{i} \frac{\rm \pi}{4} St^{*}, \quad \textrm{I}^{(2)}_q\simeq 0,\\ \textrm{I}^{(0)*}_{\partial q} & \simeq{-}\frac{\rm \pi}{4} St^{*2} - \mathrm{i} {\rm \pi}St^{*} , \quad \textrm{I}^{(1)*}_{\partial q} \simeq{-}{\rm \pi} + \mathrm{i}\frac{\rm \pi}{2}St^{*}, \quad\textrm{I}^{(2)}_{\partial q} \simeq 0,\\ \textrm{J}^{(0)*}_{\mu} & \simeq{-}\frac{\rm \pi}{4} St^{*2}-\mathrm{i}{\rm \pi} St^{*} , \quad \textrm{J}^{(1)*}_{\mu} \simeq{-}{\rm \pi} + \mathrm{i}\frac{\rm \pi}{2} St^{*}, \quad \textrm{J}^{(2)}_{\mu} \simeq 0. \end{aligned} \right\} \end{equation}
For simplicity, we consider only plane entropy waves (![]() $k_2=0$) and, thus, the computation of the integrals
$k_2=0$) and, thus, the computation of the integrals ![]() $\textrm {I}^{(0)}_{\mu }$ and
$\textrm {I}^{(0)}_{\mu }$ and ![]() $\textrm {I}^{(\,j)}_{\mu }$ is not necessary. A simple analytical description of the acoustic potential can be given as
$\textrm {I}^{(\,j)}_{\mu }$ is not necessary. A simple analytical description of the acoustic potential can be given as
which shows that the acoustic potential is the combination of a monopole and a horizontal dipole solution. The monopole, which arises from the acceleration source term, is ![]() ${O}({M_{\infty }})$ the dipole. The main contribution for the dipole term comes from the boundary integral. Physically, the dipole can be interpreted in terms of the unsteady horizontal force experienced by the blade when interacting with density fluctuations. To counter this force, an acoustic field must be generated. The monopole term, on the other hand, has its origin in the strong local acceleration produced at the leading edge of the aerofoil. Note that for
${O}({M_{\infty }})$ the dipole. The main contribution for the dipole term comes from the boundary integral. Physically, the dipole can be interpreted in terms of the unsteady horizontal force experienced by the blade when interacting with density fluctuations. To counter this force, an acoustic field must be generated. The monopole term, on the other hand, has its origin in the strong local acceleration produced at the leading edge of the aerofoil. Note that for ![]() $St^{*}> 0.5$, the values of the integrals quickly deviate from the trends shown in figure 11 and (5.10) is no longer appropriate. For these frequencies, however, the general formalism is still fully valid and results are obtained for each individual frequency.
$St^{*}> 0.5$, the values of the integrals quickly deviate from the trends shown in figure 11 and (5.10) is no longer appropriate. For these frequencies, however, the general formalism is still fully valid and results are obtained for each individual frequency.

Figure 11. Real (black solid) and imaginary (red dashed) parts of the source and boundary integrals. The results are scaled by functions of ![]() $St^{*}=St/\beta _{\infty }^{2}$ to highlight their functional dependence on this parameter.
$St^{*}=St/\beta _{\infty }^{2}$ to highlight their functional dependence on this parameter.
Figure 12 shows an example of the acoustic field predicted by the model. For ![]() $M_{\infty }=0.1,$ the acoustic field has the form of a horizontal dipole, with amplitude weakly modulated by the Doppler factor. When the Mach number is increased to
$M_{\infty }=0.1,$ the acoustic field has the form of a horizontal dipole, with amplitude weakly modulated by the Doppler factor. When the Mach number is increased to ![]() $M_{\infty }=0.5,$ the main sound radiation still happens along the horizontal axis, but the field exhibits a strong directivity in the forward direction. This arises from a combination of the Doppler factor and the monopole contribution becoming significant.
$M_{\infty }=0.5,$ the main sound radiation still happens along the horizontal axis, but the field exhibits a strong directivity in the forward direction. This arises from a combination of the Doppler factor and the monopole contribution becoming significant.

Figure 12. Normalised acoustic field, ![]() $p'/\rho _{\infty }U_{\infty }^{2},$ predicted by the model for a symmetric aerofoil at
$p'/\rho _{\infty }U_{\infty }^{2},$ predicted by the model for a symmetric aerofoil at ![]() $He=0.1$ and (a)
$He=0.1$ and (a) ![]() ${M_{\infty }}=0.1$ and (b)
${M_{\infty }}=0.1$ and (b) ![]() ${M_{\infty }}=0.5.$ See supplementary movies 1 and 2 available at https://doi.org/10.1017/jfm.2021.569.
${M_{\infty }}=0.5.$ See supplementary movies 1 and 2 available at https://doi.org/10.1017/jfm.2021.569.
The quality of the model is now assessed using the numerical results described in § 5.1. Figures 13, 14, 17 and 18 show a comparison of the predictions of the model with numerical simulations of the linearised compressible Euler equations for several Mach numbers and frequencies. The modulus of the pressure field ![]() $|p'|$ has been computed at a distance of 15 semi-chords from the profile for four different Helmholtz numbers. At low Mach numbers, figures 13 and 14 show that the agreement between computational aeroacoustics (CAA) and model predictions is excellent for all four frequencies. At low frequencies, the directivity exhibits four main lobes along the horizontal and vertical axes. This behaviour corresponds to that observed for the axial derivative of the horizontal dipole
$|p'|$ has been computed at a distance of 15 semi-chords from the profile for four different Helmholtz numbers. At low Mach numbers, figures 13 and 14 show that the agreement between computational aeroacoustics (CAA) and model predictions is excellent for all four frequencies. At low frequencies, the directivity exhibits four main lobes along the horizontal and vertical axes. This behaviour corresponds to that observed for the axial derivative of the horizontal dipole ![]() $\partial \phi _1/\partial x_1$ at low frequencies (figure 5(b,e) – second term of (3.19b)). Further from the source, the directivity pattern is similar to a dipole. At higher frequencies, the directivity clearly exhibits the behaviour of a horizontal dipole with a stronger directivity in the forward direction (accentuated with increased Mach number).
$\partial \phi _1/\partial x_1$ at low frequencies (figure 5(b,e) – second term of (3.19b)). Further from the source, the directivity pattern is similar to a dipole. At higher frequencies, the directivity clearly exhibits the behaviour of a horizontal dipole with a stronger directivity in the forward direction (accentuated with increased Mach number).

Figure 13. Model validation: far-field directivity pattern, ![]() $|p'|/\rho _{\infty }U_{\infty }^{2},$ of the analytical solution compared with numerical solutions of the Euler equations. Here,
$|p'|/\rho _{\infty }U_{\infty }^{2},$ of the analytical solution compared with numerical solutions of the Euler equations. Here, ![]() $M_{\infty }=0.1$ and Helmholtz numbers (a)
$M_{\infty }=0.1$ and Helmholtz numbers (a) ![]() $He=0.001,$ (b)
$He=0.001,$ (b) ![]() $He=0.005,$ (c)
$He=0.005,$ (c) ![]() $He=0.05$ and (d)
$He=0.05$ and (d) ![]() $He=0.1$. The observer is placed at
$He=0.1$. The observer is placed at ![]() $R_{obs}/b= 15$. Note that the axis amplitudes are different for each frequency.
$R_{obs}/b= 15$. Note that the axis amplitudes are different for each frequency.

Figure 14. Far-field directivity pattern, ![]() $|p'|/\rho _{\infty }U_{\infty }^{2},$ for
$|p'|/\rho _{\infty }U_{\infty }^{2},$ for ![]() $M_{\infty }=0.2$ and Helmholtz numbers (a)
$M_{\infty }=0.2$ and Helmholtz numbers (a) ![]() $He=0.001,$ (b)
$He=0.001,$ (b) ![]() $He=0.005,$ (c)
$He=0.005,$ (c) ![]() $He=0.05$ and (d)
$He=0.05$ and (d) ![]() $He=0.1$. The observer is placed at
$He=0.1$. The observer is placed at ![]() $R_{obs}/b= 15$.
$R_{obs}/b= 15$.
In figure 15, we explore the evolution of the acoustic pressure as a function of the frequency for a fixed observer. At low frequencies (![]() $St<0.5$), (5.10) shows that the acoustic potential increases linearly with the frequency. Combining this with (3.18), we obtain the quadratic growth of the acoustic pressure observed in figure 15. For
$St<0.5$), (5.10) shows that the acoustic potential increases linearly with the frequency. Combining this with (3.18), we obtain the quadratic growth of the acoustic pressure observed in figure 15. For ![]() $St > 0.5,$ the pressure keeps increasing for increasing frequencies with a seemingly linear dependence. At
$St > 0.5,$ the pressure keeps increasing for increasing frequencies with a seemingly linear dependence. At ![]() $St \simeq 1.5$ this linear growth saturates and a maximum value of the pressure is obtained at around
$St \simeq 1.5$ this linear growth saturates and a maximum value of the pressure is obtained at around ![]() $St \simeq 2.5.$ The pressure then drops reaching a local minimum at
$St \simeq 2.5.$ The pressure then drops reaching a local minimum at ![]() $St \simeq 4.25.$ All these trends are qualitatively well-described by the model. Quantitatively, the predictions of the model are in excellent agreement with the numerical results up to
$St \simeq 4.25.$ All these trends are qualitatively well-described by the model. Quantitatively, the predictions of the model are in excellent agreement with the numerical results up to ![]() $He \approx 0.2,$ after which the performance of the model slowly deteriorates. This is in agreement with the range of validity of the compact Green's function (valid for
$He \approx 0.2,$ after which the performance of the model slowly deteriorates. This is in agreement with the range of validity of the compact Green's function (valid for ![]() $He^{2} \ll 1).$ Figure 16 shows the directivity for a frequency which is beyond the range of validity of the analytical solution, namely
$He^{2} \ll 1).$ Figure 16 shows the directivity for a frequency which is beyond the range of validity of the analytical solution, namely ![]() $He=0.5.$ Although a certain mismatch is observed, the directivity pattern is generally well-described (especially for
$He=0.5.$ Although a certain mismatch is observed, the directivity pattern is generally well-described (especially for ![]() ${M_{\infty }}=0.1$).
${M_{\infty }}=0.1$).

Figure 15. Limits of validity of the model: normalised acoustic pressure, ![]() $|p'|/\rho _{\infty }U_{\infty }^{2},$ for an observer placed at
$|p'|/\rho _{\infty }U_{\infty }^{2},$ for an observer placed at ![]() $(x_1,\; x_2) = (-15 b,0)$. The grey area corresponds to the domain of validity of (5.10). (a)
$(x_1,\; x_2) = (-15 b,0)$. The grey area corresponds to the domain of validity of (5.10). (a) ![]() $M_{\infty }=0.1$ and (b)
$M_{\infty }=0.1$ and (b) ![]() $M_{\infty }=0.2.$
$M_{\infty }=0.2.$

Figure 16. Limits of validity of the model: far-field directivity pattern, ![]() $|p'|/\rho _{\infty }U_{\infty }^{2},$ for
$|p'|/\rho _{\infty }U_{\infty }^{2},$ for ![]() $He=0.5,$ and (a)
$He=0.5,$ and (a) ![]() $M_{\infty }=0.1$ and (b)
$M_{\infty }=0.1$ and (b) ![]() $M_{\infty }=0.2.$
$M_{\infty }=0.2.$
Figures 17 and 18 show directivity plots for ![]() $M_{\infty }=0.5$ and
$M_{\infty }=0.5$ and ![]() $0.7,$ respectively. At low frequencies, the four-lobes directivity pattern persists. At higher frequencies, the pressure presents a very strong directivity in the forward direction owing to a combination of the Doppler effect and the monopole source created at the leading edge. These figures also show that the performance of the model slowly degrades with increasing Mach number. For
$0.7,$ respectively. At low frequencies, the four-lobes directivity pattern persists. At higher frequencies, the pressure presents a very strong directivity in the forward direction owing to a combination of the Doppler effect and the monopole source created at the leading edge. These figures also show that the performance of the model slowly degrades with increasing Mach number. For ![]() $M_{\infty }=0.5,$ the predictions for both directivity and amplitude are acceptable, even if not as good as for the previous cases. For
$M_{\infty }=0.5,$ the predictions for both directivity and amplitude are acceptable, even if not as good as for the previous cases. For ![]() $M_{\infty }=0.7,$ the directivity is still correctly predicted, but the model underestimates the pressure amplitude by a factor of approximately two. The disagreement most probably arises from errors in the mean flow model. As explained in § 5.2, we observe a mismatch between the numerical and the theoretical normalised pressure coefficient for
$M_{\infty }=0.7,$ the directivity is still correctly predicted, but the model underestimates the pressure amplitude by a factor of approximately two. The disagreement most probably arises from errors in the mean flow model. As explained in § 5.2, we observe a mismatch between the numerical and the theoretical normalised pressure coefficient for ![]() $M_{\infty }=0.7,$ which becomes quite significant close to the stagnation point of the aerofoil, where the main source of noise resides.
$M_{\infty }=0.7,$ which becomes quite significant close to the stagnation point of the aerofoil, where the main source of noise resides.

Figure 17. Far-field directivity pattern, ![]() $|p'|/\rho _{\infty }U_{\infty }^{2},$ for
$|p'|/\rho _{\infty }U_{\infty }^{2},$ for ![]() $M_{\infty }=0.5$ and Helmholtz numbers (a)
$M_{\infty }=0.5$ and Helmholtz numbers (a) ![]() $He=0.001,$ (b)
$He=0.001,$ (b) ![]() $He=0.005,$ (c)
$He=0.005,$ (c) ![]() $He=0.05$ and (d)
$He=0.05$ and (d) ![]() $He=0.1$. The observer is placed at
$He=0.1$. The observer is placed at ![]() $R_{obs}/b= 15$.
$R_{obs}/b= 15$.

Figure 18. Far-field directivity pattern, ![]() $|p'|/\rho _{\infty }U_{\infty }^{2},$ for
$|p'|/\rho _{\infty }U_{\infty }^{2},$ for ![]() $M_{\infty }=0.7$ and Helmholtz numbers (a)
$M_{\infty }=0.7$ and Helmholtz numbers (a) ![]() $He=0.001,$ (b)
$He=0.001,$ (b) ![]() $He=0.005,$ (c)
$He=0.005,$ (c) ![]() $He=0.05$ and (d)
$He=0.05$ and (d) ![]() $He=0.1$. The observer is placed at
$He=0.1$. The observer is placed at ![]() $R_{obs}/b= 15$.
$R_{obs}/b= 15$.
6. Summary and conclusions
A theoretical model for the sound generated by entropy perturbations interacting with blades has been introduced. The model is based on a linearisation of the compressible Euler equations about a steady, potential mean flow. Using the Born approximation, it has been shown that for thin aerofoils, the sound can be assumed to propagate in a uniform mean flow. This assumption is also valid for thick and strongly cambered aerofoils at the expense of the range of validity in frequency and Mach number. Using a Lorentz-type transformation, the governing equations have been reduced to the Helmholtz equation that has been solved using a low-frequency Green's function. The approach assumes that the acoustic wavelength is large compared to the chord of the profile, but it places no restriction on the entropy wavelength. The source term has been simplified using thin-aerofoil theory and results have been obtained for a symmetric aerofoil, showing good agreement between the model and numerical simulations of the linearised compressible Euler equations. The results show that the acoustic field generated when this aerofoil interacts with plane entropy waves corresponds to a dipole along the horizontal axis, in agreement with the conclusions of Bodony (Reference Bodony2009), and an additional monopole term that becomes apparent only at high Mach numbers.
This work represents an extension to low frequencies of existing solutions using high-frequency asymptotics (Kerschen & Myers Reference Kerschen and Myers1987; Tsai Reference Tsai1992; Myers & Kerschen Reference Myers and Kerschen1995, Reference Myers and Kerschen1997). Solutions in the thin-aerofoil limit are now available for all range of frequencies for symmetric aerofoils. An extension of the current theory to lifting aerofoils is currently under investigation and will be the subject of future publications.
An advantage of the approach proposed here is that it can be extended to aerofoils beyond the limits of thin-aerofoil theory. This is of practical interest for the modelling of blades in realistic turbine cascades, where the favourable pressure gradient allows for larger angles of attack, cambers and thickness of the aerofoils. This extension presents some difficulties, the most important being that the source term and boundary conditions become singular along the aerofoil and wake. This problem was addressed by Atassi & Grzedzinski (Reference Atassi and Grzedzinski1989) who proposed an alternative splitting of the velocity field more suitable for numerical applications (Scott & Atassi Reference Scott and Atassi1995; Scott, Atassi & Susan-Resiga Reference Scott, Atassi and Susan-Resiga2003). An extension of the model proposed here is actively being developed using Atassi's formulation together with a boundary element method (Zhong et al. Reference Zhong, Jiang, Ying, Zhang and Huang2019).
Entropy noise is relevant in the context of turbomachinery for which the current approach requires an extension to cascades with finite blockage ratio. This challenge will be addressed in a forthcoming study and involves the separation of the domain into upstream, downstream and interblade regions and the use of periodic Green's functions (Linton Reference Linton1998).
Supplementary material
Supplementary movies are available at https://doi.org/10.1017/jfm.2021.569.
Acknowledgements
A preliminary version of this work was presented at AIAA Aviation as Guzmán-Iñigo, Duran & Morgans (Reference Guzmán-Iñigo, Duran and Morgans2018). J.G. gratefully acknowledges Dong Yang for valuable advice.
Funding
The authors would like to gratefully acknowledge the European Research Council (ERC) Starting Grant ACOULOMODE (2013–2018) and the ERC Consolidator Grant AFIRMATIVE (2018–2023) for supporting the current research.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Validity of the Born approximation
In this Appendix, we study the conditions of validity of the Born approximation for the ‘time-reduced’ convected wave equation (3.2). To this end, we start from the first-order approximation of the acoustic potential and we substitute the integral solution of (3.5), to obtain:
Then, we normalise the wavenumber and Mach number inhomogeneities as ![]() $\kappa _{\varDelta }=\kappa _{\infty }\delta \kappa$ and
$\kappa _{\varDelta }=\kappa _{\infty }\delta \kappa$ and ![]() $\boldsymbol {M}_{\varDelta } = M_{\infty } \delta \boldsymbol {M}.$ Neglecting
$\boldsymbol {M}_{\varDelta } = M_{\infty } \delta \boldsymbol {M}.$ Neglecting ![]() $\mathcal {L}_0,$ (A1) can be recast as
$\mathcal {L}_0,$ (A1) can be recast as
 $$\begin{align} \hat
\phi(\boldsymbol{x}) &= \hat \phi_{\infty} - \int_{{V}}
\left[ (\kappa_{\infty} \delta \kappa)^{2} + 2\mathrm{i}
\kappa_{\infty}M_{\infty}\delta \kappa \delta
\boldsymbol{M} \boldsymbol{\cdot} \boldsymbol{\nabla}-
M_{\infty}^{2} \delta \boldsymbol{M} \boldsymbol{\cdot}
\left( \delta \boldsymbol{M} \boldsymbol{\cdot}
\boldsymbol{\nabla} \boldsymbol{\nabla} \right)
\phantom{\frac{\partial}{\partial x_1}} \right.\nonumber\\
&\quad \left. +\, 2\left( \kappa_{\infty}^{2}\delta \kappa +
\mathrm{i} \kappa_{\infty} M_{\infty} \delta \boldsymbol{M}
\boldsymbol{\cdot} \boldsymbol{\nabla} + \mathrm{i}
\kappa_{\infty} M_{\infty} \delta \kappa
\frac{\partial}{\partial x_1} - M_{\infty}^{2} \delta M
\frac{\partial}{\partial x_1} \boldsymbol{\nabla} \right)
\right] G \, \textrm{d} V.
\end{align}$$
$$\begin{align} \hat
\phi(\boldsymbol{x}) &= \hat \phi_{\infty} - \int_{{V}}
\left[ (\kappa_{\infty} \delta \kappa)^{2} + 2\mathrm{i}
\kappa_{\infty}M_{\infty}\delta \kappa \delta
\boldsymbol{M} \boldsymbol{\cdot} \boldsymbol{\nabla}-
M_{\infty}^{2} \delta \boldsymbol{M} \boldsymbol{\cdot}
\left( \delta \boldsymbol{M} \boldsymbol{\cdot}
\boldsymbol{\nabla} \boldsymbol{\nabla} \right)
\phantom{\frac{\partial}{\partial x_1}} \right.\nonumber\\
&\quad \left. +\, 2\left( \kappa_{\infty}^{2}\delta \kappa +
\mathrm{i} \kappa_{\infty} M_{\infty} \delta \boldsymbol{M}
\boldsymbol{\cdot} \boldsymbol{\nabla} + \mathrm{i}
\kappa_{\infty} M_{\infty} \delta \kappa
\frac{\partial}{\partial x_1} - M_{\infty}^{2} \delta M
\frac{\partial}{\partial x_1} \boldsymbol{\nabla} \right)
\right] G \, \textrm{d} V.
\end{align}$$
Let us now assume a three-dimensional domain for simplicity of the following discussions. If the size of the scatterer is of order ![]() $L,$ then by dimensional analysis,
$L,$ then by dimensional analysis,
For the Born approximation to be valid it is required that ![]() $\hat \phi _{\varDelta } \ll \hat \phi _{\infty }$ which, using (A2), leads to the following conditions:
$\hat \phi _{\varDelta } \ll \hat \phi _{\infty }$ which, using (A2), leads to the following conditions:
 $$\begin{gather} (\kappa_{\infty}L)^{2} \delta \kappa ^{2}\ll 1, \quad (\kappa_{\infty}L) M_{\infty} \; \delta\kappa \; \delta M \ll 1,\quad M_{\infty}^{2} \; \delta M^{2} \ll 1, \quad (\kappa_{\infty}L)^{2} \; \delta \kappa \ll 1,\nonumber\\ (\kappa_{\infty}L)\; M_{\infty} \; \delta M \ll 1, \quad (\kappa_{\infty}L)\; M_{\infty} \; \delta \kappa \ll 1 \quad \text{and} \quad M_{\infty}^{2} \; \delta M \ll 1, \end{gather}$$
$$\begin{gather} (\kappa_{\infty}L)^{2} \delta \kappa ^{2}\ll 1, \quad (\kappa_{\infty}L) M_{\infty} \; \delta\kappa \; \delta M \ll 1,\quad M_{\infty}^{2} \; \delta M^{2} \ll 1, \quad (\kappa_{\infty}L)^{2} \; \delta \kappa \ll 1,\nonumber\\ (\kappa_{\infty}L)\; M_{\infty} \; \delta M \ll 1, \quad (\kappa_{\infty}L)\; M_{\infty} \; \delta \kappa \ll 1 \quad \text{and} \quad M_{\infty}^{2} \; \delta M \ll 1, \end{gather}$$
where ![]() $\delta M$ is the modulus of
$\delta M$ is the modulus of ![]() $\delta \boldsymbol {M}.$
$\delta \boldsymbol {M}.$
Appendix B. Derivation of the integral formulation
An integral solution to (3.8a,b) is derived here. To this end, we first introduce the free-space Green's function of (3.8a,b), that is,
Next, we can form a weighted residual integral for (3.8a,b), by weighting it by this Green's function and integrating over the volume of interest. After some manipulations, we obtain:
 \begin{equation} \tilde \phi(\boldsymbol{x}) = \int_{{V}} \tilde S G \, \textrm{d} V + \int_{{S}} \left( G \frac{\partial \tilde \phi}{\partial \tilde{\boldsymbol{n}}} - \tilde \phi \frac{\partial G}{\partial \tilde{\boldsymbol{n}}} \right)\, \textrm{d} S. \end{equation}
\begin{equation} \tilde \phi(\boldsymbol{x}) = \int_{{V}} \tilde S G \, \textrm{d} V + \int_{{S}} \left( G \frac{\partial \tilde \phi}{\partial \tilde{\boldsymbol{n}}} - \tilde \phi \frac{\partial G}{\partial \tilde{\boldsymbol{n}}} \right)\, \textrm{d} S. \end{equation}
We now introduce the potential ![]() $\hat \phi$ in the surface integrals to obtain:
$\hat \phi$ in the surface integrals to obtain:
To obtain a closed-form integral solution, a Green's function that cancels the second surface integral on the aerofoil has to be obtained, hence the boundary condition that we impose on (3.9a,b).
Appendix C. Numerical convergence of the improper integrals
First, we prove analytically the convergence of ![]() $\textrm {I}_{q}^{(1)},$ i.e.
$\textrm {I}_{q}^{(1)},$ i.e.
 \begin{align} \textrm{I}^{(1)}_q &=
\frac{1}{\beta_{\infty}^{2}}\int_{{V}} q Y_1
\,\textrm{e}^{\mathrm{i} \sigma} \,
\textrm{d}{\bar{x}_1}\textrm{d}{\bar{x}_2}\nonumber\\
&= \frac{b^{3}}{4\beta_{\infty}^{4}}\int_{{V}}\left[
\mathrm{Re} \left(-\frac{1}{\tau^{2}} +
\frac{1}{|\tau|^{4}} + \frac{1}{\tau^{3}} -
\frac{1}{|\tau|^{4}\tau}\right)\right.\nonumber\\ &\quad
\times \left. \mathrm{Re} \left( \tau + \frac{1}{\tau}
\right)\exp{\left(\mathrm{i}
\frac{St}{2\beta_{\infty}^{2}}\mathrm{Re} \left( \tau +
\frac{1}{\tau} \right) \right)} \right] \,
\textrm{d}{\tau_1}\textrm{d}{\tau_2}.
\end{align}
\begin{align} \textrm{I}^{(1)}_q &=
\frac{1}{\beta_{\infty}^{2}}\int_{{V}} q Y_1
\,\textrm{e}^{\mathrm{i} \sigma} \,
\textrm{d}{\bar{x}_1}\textrm{d}{\bar{x}_2}\nonumber\\
&= \frac{b^{3}}{4\beta_{\infty}^{4}}\int_{{V}}\left[
\mathrm{Re} \left(-\frac{1}{\tau^{2}} +
\frac{1}{|\tau|^{4}} + \frac{1}{\tau^{3}} -
\frac{1}{|\tau|^{4}\tau}\right)\right.\nonumber\\ &\quad
\times \left. \mathrm{Re} \left( \tau + \frac{1}{\tau}
\right)\exp{\left(\mathrm{i}
\frac{St}{2\beta_{\infty}^{2}}\mathrm{Re} \left( \tau +
\frac{1}{\tau} \right) \right)} \right] \,
\textrm{d}{\tau_1}\textrm{d}{\tau_2}.
\end{align}
The integrand can be evaluated asymptotically yielding
Because ![]() $|{\exp {(\mathrm {i} ({St}/{2\beta _{\infty }^{2}}) \tau )}}| < 1,$ we can use the comparison test and the absolute convergence test to recast the convergence of the previous integral as the convergence of
$|{\exp {(\mathrm {i} ({St}/{2\beta _{\infty }^{2}}) \tau )}}| < 1,$ we can use the comparison test and the absolute convergence test to recast the convergence of the previous integral as the convergence of
which, using the cylindrical change of coordinates ![]() $\tau =r \,\textrm {e}^{\mathrm {i} \theta },$ is integrated to yield
$\tau =r \,\textrm {e}^{\mathrm {i} \theta },$ is integrated to yield
hence proving the convergence of (C1). This integral has the largest integrand among all the integrals arising in § 5, which proves through the comparison test that all of the integrals converge.
We now turn our attention to the numerical convergence of the integrals. To numerically approximate them, we truncate the limit ![]() $r\to \infty$ to a finite value
$r\to \infty$ to a finite value ![]() $R_{{max}}.$ For example, for (5.7), we compute
$R_{{max}}.$ For example, for (5.7), we compute
Figure 19 shows that the integrals ![]() $\textrm {I}^{(0)}_{q},$
$\textrm {I}^{(0)}_{q},$ ![]() $\textrm {I}^{(0)}_{\partial q}$ and
$\textrm {I}^{(0)}_{\partial q}$ and ![]() $\textrm {I}^{(1)}_{\partial q}$ can be considered converged when we integrate over a domain extending to
$\textrm {I}^{(1)}_{\partial q}$ can be considered converged when we integrate over a domain extending to ![]() $R_{{max}}\approx 10^{4}.$ Despite the apparent large extension of the domain, these calculations can be obtained within minutes. The integral
$R_{{max}}\approx 10^{4}.$ Despite the apparent large extension of the domain, these calculations can be obtained within minutes. The integral ![]() $\textrm {I}^{(1)}_{q}$, in contrast, requires a domain as large as
$\textrm {I}^{(1)}_{q}$, in contrast, requires a domain as large as ![]() $R_{{max}}\approx 10^{8}$ for its imaginary part to be converged. Because the area to be integrated is proportional to
$R_{{max}}\approx 10^{8}$ for its imaginary part to be converged. Because the area to be integrated is proportional to ![]() $R_{{max}}^{2},$ the cost becomes prohibitive for this integral. To alleviate this problem, after a certain value of
$R_{{max}}^{2},$ the cost becomes prohibitive for this integral. To alleviate this problem, after a certain value of ![]() $r=R_0,$ the integral was approximated using the asymptotic representation given by (C2), which in cylindrical coordinates reads
$r=R_0,$ the integral was approximated using the asymptotic representation given by (C2), which in cylindrical coordinates reads
This expression can be integrated over ![]() $r$ yielding
$r$ yielding

Figure 19. Convergence of the source integrals for ![]() $St=0.1.$ Real (black solid) and imaginary (red dashed) parts of the integrals (a)
$St=0.1.$ Real (black solid) and imaginary (red dashed) parts of the integrals (a) ![]() $\textrm {I}^{(0)}_{q}$, (b)
$\textrm {I}^{(0)}_{q}$, (b) ![]() $\textrm {I}^{(1)}_{q}$, (c)
$\textrm {I}^{(1)}_{q}$, (c) ![]() $\textrm {I}^{(0)}_{\partial q}$ and (d)
$\textrm {I}^{(0)}_{\partial q}$ and (d) ![]() $\textrm {I}^{(1)}_{\partial q}.$ The dotted line in (b) corresponds to the asymptotic evaluation of the integral. Both the exact and asymptotic integrals are depicted in the grey area.
$\textrm {I}^{(1)}_{\partial q}.$ The dotted line in (b) corresponds to the asymptotic evaluation of the integral. Both the exact and asymptotic integrals are depicted in the grey area.