Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-07-04T12:07:14.443Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling of space–time modes with Reynolds number in two-dimensional turbulence

Published online by Cambridge University Press:  14 October 2021

N. K.-R. Kevlahan ,
J. Alam  and
O. V. Vasilyev
N. K.-R. Kevlahan
Affiliation:
Department of Mathematics & Statistics, McMaster University, Hamilton L8S 4K1, Canada
J. Alam
Affiliation:
Department of Mathematics & Statistics, McMaster University, Hamilton L8S 4K1, Canada
O. V. Vasilyev
Affiliation:
Department of Mechanical Engineering, University of Colorado, Boulder, CO 80309, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

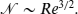It has been estimated that the number of spatial modes (or nodal values) required to uniquely determine a two-dimensional turbulent flow at a specific time is finite, and is bounded by Re4/3 for forced turbulence and Re for decaying turbulence. The usual computational estimate of the number of space–time modes required to calculated decaying two-dimensional turbulence is . These bounds neglect intermittency, and it is not known how sharp they are. In this paper we use an adaptive multi-scale wavelet collocation method to estimate for the first time the number of space–time computational modes necessary to represent two-dimensional decaying turbulence as a function of Reynolds number. We find that 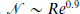for 1260 ≤ Re ≤ 40400 over many eddy turn-over times, and that temporal intermittency is stronger than spatial intermittency. The spatial modes alone scale like Re0.7. The β-model then implies that the spatial fractal dimension of the active regions is 1.2, and the temporal fractal dimension is 0.3. These results suggest that the usual estimates are not sharp for adaptive numerical simulations. The relatively high compression confirms the importance of intermittency and encourages the search for reduced mathematical models of two-dimensional turbulence (e.g. in terms of coherent vortices).

Type
Research Article
Information
Journal of Fluid Mechanics , Volume 570 , 10 January 2007 , pp. 217 - 226
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alam, J., Kevlahan, N. K.-R. & Vasilyev, O. V. 2006 Simultaneous space–time adaptive wavelet solution of nonlinear partial differential equations. J. Comput. Phys. 214, 829–857.CrossRefGoogle Scholar
Constantin, P. 1985 Attractors representing turbulent flows. Mem. Am. Math. Soc. 53 (314), 1–67.Google Scholar
Constantin, P., Foias, C. & Temam, R. 1988 On the dimension of the attractors in two-dimensional turbulence. Physica D 30, 284–296.CrossRefGoogle Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Doering, C. R. & Foias, C. 2002 Energy dissipation in body-forced turbulence. J. Fluid Mech. 467, 289–306.CrossRefGoogle Scholar
Farge, M., Schneider, K. & Kevlahan, N. K.-R. 1999 Non-Gaussianity and coherent vortex simulation for two-dimensional turbulence using an adaptive orthogonal wavelet basis. Phys. Fluids 11, 2187–2201.CrossRefGoogle Scholar
Foias, C. & Prodi, G. 1967 Sur le comportement global des solution non stationnaires des équations de Navier–Stokes en dimension deux. Rend. Sem. Math. Univ. Padova 39, 1–34.Google Scholar
Foias, C. & Temam, R. 1984 Determination of the solutions of the Navier–Stokes equations by a set of nodal values. Math. Comput. 43, 117–133.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Frisch, U., Nelkin, M. & Sulem, P.-L. 1978 A simple dynamical model of intermittent fully developed turbulence. J. Fluid Mech. 87, 719–736.10.1017/S0022112078001846CrossRefGoogle Scholar
Friz, P. K. & Robinson, J. C. 2001 Parametrising the attractor of the two-dimensional Navier–Stokes equations with a finite number of nodal values. Physica D 148, 201–220.CrossRefGoogle Scholar
Galdi, G. P. 2006 Determining modes, nodes and volume elements for stationary solutions of the Navier–Stokes problem past a three-dimensional body. Arch. Rat. Mech. Anal. 180, 97–126.10.1007/s00205-005-0395-0CrossRefGoogle Scholar
Jones, D. A. & Titi, E. S. 1993 Upper bounds on the number of determining modes, nodes and volume elements for the Navier–Stokes equations. Indiana Univ. Math. J. 42, 875–887.Google Scholar
Kevlahan, N. & Vasilyev, O. 2005 An adaptive wavelet collocation method for fluid–structure interaction at high Reynolds numbers. SIAM J. Sci. Comput. 26, 1894–1915.10.1137/S1064827503428503CrossRefGoogle Scholar
Kevlahan, N. K.-R. & Wadsley, J. 2005 Suppression of three-dimensional flow instabilities in tube bundles. J. Fluids Struc. 20, 611–620.CrossRefGoogle Scholar
Martin, B. K., Wu, X. L., Goldburg, W. I. & Rutgers, M. A. 1998 Spectra of decaying turbulence in a soap film. Phys. Rev. Lett. 80 (18), 3964–3967.10.1103/PhysRevLett.80.3964CrossRefGoogle Scholar
Paladin, G. & Vulpiani, A. 1987 Degrees of freedom of turbulence. Phys. Rev. A 35, 1971–1973.CrossRefGoogle ScholarPubMed
Tran, C. V., Shepherd, T. G. & Cho, H. R. 2004 Extensivity of two-dimensional turbulence. Physica D 192, 187–195.CrossRefGoogle Scholar
Vasilyev, O. V. 2003 Solving multi-dimensional evolution problems with localized structures using second generation wavelets. Intl J. Comput. Fluid Dyn. 17, 151–168.CrossRefGoogle Scholar
Vasilyev, O. V. & Kevlahan, N. K.-R. 2005 An adaptive multilevel wavelet collocation method for elliptic problems. J. Comput. Phys. 206, 412–431.CrossRefGoogle Scholar
Vincent, A. & Meneguzzi, M. 1991 The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.CrossRefGoogle Scholar
Yakhot, V. & Sreenivasan, K. R. 2005 Anomalous scaling of structure functions and dynamic constraints on turbulence simulations. J. Stat. Phys. 121, 823–841.10.1007/s10955-005-8666-6CrossRefGoogle Scholar