Article contents
Optimal inflow boundary condition perturbations in steady stenotic flow
Published online by Cambridge University Press: 01 March 2012
Abstract
We determine optimal inflow boundary perturbations to steady flow through a straight inflexible tube with a smooth axisymmetric stenosis at a bulk-flow Reynolds number 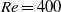 , for which the flow is asymptotically stable. The perturbations computed produce an optimal gain, i.e. kinetic energy in the domain at a given time horizon normalized by a measure of time-integrated energy on the inflow boundary segment. We demonstrate that similarly to the optimal initial condition problem, the gain can be interpreted as the leading singular value of the forward linearized operator that evolves the boundary conditions to the final state at a fixed time. In this investigation we restrict our attention to problems where the temporal profile of the perturbations examined is a product of a Gaussian bell and a sinusoid, whose frequency is selected to excite axial wavelengths similar to those of the optimal initial perturbations in the same geometry. Comparison of the final state induced by the optimal boundary perturbation with that induced by the optimal initial condition demonstrates a close agreement for the selected problem. Previous works dealing with optimal boundary perturbation considered a prescribed spatial structure and computed an optimal temporal variation of a wall-normal velocity component, whereas in this paper we consider the problem of a prescribed temporal structure and compute the optimal spatial variation of velocity boundary conditions over a one-dimensional inflow boundary segment. The methodology is capable of optimizing boundary perturbations in general non-parallel two- and three-dimensional flows.
, for which the flow is asymptotically stable. The perturbations computed produce an optimal gain, i.e. kinetic energy in the domain at a given time horizon normalized by a measure of time-integrated energy on the inflow boundary segment. We demonstrate that similarly to the optimal initial condition problem, the gain can be interpreted as the leading singular value of the forward linearized operator that evolves the boundary conditions to the final state at a fixed time. In this investigation we restrict our attention to problems where the temporal profile of the perturbations examined is a product of a Gaussian bell and a sinusoid, whose frequency is selected to excite axial wavelengths similar to those of the optimal initial perturbations in the same geometry. Comparison of the final state induced by the optimal boundary perturbation with that induced by the optimal initial condition demonstrates a close agreement for the selected problem. Previous works dealing with optimal boundary perturbation considered a prescribed spatial structure and computed an optimal temporal variation of a wall-normal velocity component, whereas in this paper we consider the problem of a prescribed temporal structure and compute the optimal spatial variation of velocity boundary conditions over a one-dimensional inflow boundary segment. The methodology is capable of optimizing boundary perturbations in general non-parallel two- and three-dimensional flows.
- Type
- Papers
- Information
- Journal of Fluid Mechanics , Volume 705: Special issue dedicated to Professor T. J. Pedley on his 70th birthday , 25 August 2012 , pp. 306 - 321
- Copyright
- Copyright © Cambridge University Press 2012
References
- 15
- Cited by




