No CrossRef data available.
Article contents
On the low-frequency flapping motion in flow separation
Published online by Cambridge University Press: 12 April 2024
Abstract
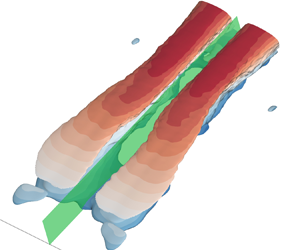
Transitional separating flow induced by a rectangular plate subjected to uniform incoming flow at Reynolds number (based on the incoming velocity and half plate height) 2000 is investigated using direct numerical simulation. The objective is to unveil the long-lasting mystery of low-frequency flapping motion (FM) in flow separation. At a fixed streamwise-vertical plane or from the perspective of previous experimental studies using pointwise or planar measurements, FM manifests as a low-frequency periodic switching between low and high velocities covering the entire separation bubble. The results indicate that in three-dimensional space, FM reflects an intricate evolution of streamwise elongated streaky structures under the influence of separated shear layer and mean flow reversal. The FM is an absolute instability, and is initiated through a lift-up mechanism boosted by mean flow deceleration near the crest of the separating streamline. At this particular location, the shear bends the vortex filament abruptly, so that one end is vertically struck into the first half of the separation bubble, whereas the other end is extended in the streamwise direction in the second half of the separation bubble. These two ends of vortex filament are mutually sustained and also stretched by the vertical acceleration and streamwise acceleration in the first and second halves of the separation bubble, respectively. This process periodically switches the low-velocity (or high-velocity) streaky structure to a high-velocity (or low-velocity) streaky structure encompassing the entire separation bubble, and thus flaps the separated shear layer up and down in the vertical direction. A ‘large vortex’ shedding manifests when the streaky structure switches signs. This large vortex is fundamentally different from the spanwise vortex shedding residing in the shear layer originated from the Kelvin–Helmholtz instability and successive vortex amalgamation. It is also believed that the three-dimensional evolution of streaky structures in the form of FM is applicable for both geometry- and pressure-induced separating flows.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press





