Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-16T23:53:38.171Z Has data issue: false hasContentIssue false
  • English
  • Français

On the late-time growth of the two-dimensional Richtmyer–Meshkov instability in shock tube experiments

Published online by Cambridge University Press:  01 October 2012

Robert V. Morgan ,
R. Aure ,
J. D. Stockero ,
J. A. Greenough ,
W. Cabot ,
O. A. Likhachev  and
J. W. Jacobs
Robert V. Morgan*
Affiliation:
Department of Aerospace and Mechanical Engineering, The University of Arizona, Tucson, AZ 85721, USA
R. Aure
Affiliation:
Department of Aerospace and Mechanical Engineering, The University of Arizona, Tucson, AZ 85721, USA
J. D. Stockero
Affiliation:
Department of Aerospace and Mechanical Engineering, The University of Arizona, Tucson, AZ 85721, USA
J. A. Greenough
Affiliation:
Lawrence Livermore National Laboratory, Livermore, CA 94550, USA
W. Cabot
Affiliation:
Lawrence Livermore National Laboratory, Livermore, CA 94550, USA
O. A. Likhachev
Affiliation:
Department of Aerospace and Mechanical Engineering, The University of Arizona, Tucson, AZ 85721, USA
J. W. Jacobs
Affiliation:
Department of Aerospace and Mechanical Engineering, The University of Arizona, Tucson, AZ 85721, USA
*
†Email address for correspondence: rvm@email.arizona.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present study, shock tube experiments are used to study the very late-time development of the Richtmyer–Meshkov instability from a diffuse, nearly sinusoidal, initial perturbation into a fully turbulent flow. The interface is generated by two opposing gas flows and a perturbation is formed on the interface by transversely oscillating the shock tube to create a standing wave. The puncturing of a diaphragm generates a Mach 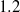$1. 2$ shock wave that then impacts a density gradient composed of air and SF6, causing the Richtmyer–Meshkov instability to develop in the 2.0 m long test section. The instability is visualized with planar Mie scattering in which smoke particles in the air are illuminated by a Nd:YLF laser sheet, and images are recorded using four high-speed video cameras operating at 6 kHz that allow the recording of the time history of the instability. In addition, particle image velocimetry (PIV) is implemented using a double-pulsed Nd:YAG laser with images recorded using a single CCD camera. Initial modal content, amplitude, and growth rates are reported from the Mie scattering experiments while vorticity and circulation measurements are made using PIV. Amplitude measurements show good early-time agreement but relatively poor late-time agreement with existing nonlinear models. The model of Goncharov (Phys. Rev. Lett., vol. 88, 2002, 134502) agrees with growth rate measurements at intermediate times but fails at late experimental times. Measured background acceleration present in the experiment suggests that the late-time growth rate may be influenced by Rayleigh–Taylor instability induced by the interfacial acceleration. Numerical simulations conducted using the LLNL codes Ares and Miranda show that this acceleration may be caused by the growth of boundary layers, and must be accounted for to produce good agreement with models and simulations. Adding acceleration to the Richtmyer–Meshkov buoyancy–drag model produces improved agreement. It is found that the growth rate and amplitude trends are also modelled well by the Likhachev–Jacobs vortex model (Likhachev & Jacobs, Phys. Fluids, vol. 17, 2005, 031704). Circulation measurements also show good agreement with the circulation value extracted by fitting the vortex model to the experimental data.

JFM classification

Compressible Flows: Compressible Flows Instability: Instability Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 712 , 10 December 2012 , pp. 354 - 383
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Roxar Flow Measurement, Gamle Forusvei 17, 4065 Stavanger, Norway.

§

Present address: Lockheed Martin Aeronautics, 1011 Lockheed Way, Palmdale, CA 93599.

References

Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. National Bureau of Standards Applied Mathematics Series.CrossRefGoogle Scholar
Aure, R. & Jacobs, J. W 2008 Particle image velocimetry study of the shock-induced single mode Richtmyer–Meshkov instability. Shock Waves 18, 161–167.CrossRefGoogle Scholar
Badcock, K. J. 1992 A numerical simulation of boundary layer effects in a shock tube. Intl J. Numer. Meth. Fluids 14, 1151–1171.CrossRefGoogle Scholar
Balakumar, B. J., Orlicz, G. C., Tomkins, C. D. & Prestridge, K. P. 2008 Dependence of growth patterns and mixing width on initial conditions in Richtmyer–Meshkov unstable fluid layers. Phys. Scr. T123, 014013.CrossRefGoogle Scholar
Benjamin, R. F., Trease, H. E. & Shaner, J. W. 1984 Coherent density gradients in water compressed by a modulated shock wave. Phys. Fluids 27, 2390–2393.CrossRefGoogle Scholar
Bonazza, R. & Sturtevant, B. 1996 X-ray measurements of growth rates at a gas interface accelerated by shock waves. Phys. Fluids 8, 2496–2512.CrossRefGoogle Scholar
Brocher, E. F. 1964 Hot flow length and testing time in real shock tube flow. Phys. Fluids 7, 347–351.CrossRefGoogle Scholar
Collins, B. D. & Jacobs, J. W. 2002 PLIF flow visualization and measurements of the Richtmyer–Meshkov instability of an air/ ${\mathrm{SF} }_{6} $ interface. J. Fluid Mech. 464, 113–136.CrossRefGoogle Scholar
Cook, A. W. 2007 Artificial fluid properties for large-eddy simulation of compressible turbulent mixing. Phys. Fluids 19, 055103.CrossRefGoogle Scholar
Cook, A. W. & Cabot, W. H. 2004 A high-wavenumber viscosity for high-resolution numerical methods. J. Comput. Phys. 195, 594–601.CrossRefGoogle Scholar
Cook, A. W. & Cabot, W. H. 2005 Hyperviscosity for shock–turbulence interactions. J. Comput. Phys. 203, 379–385.CrossRefGoogle Scholar
Dimonte, G. & Ramaprabhu, P. 2010 Simulations and model of the nonlinear Richtmyer–Meshkov instability. Phys. Fluids 22, 4014104.CrossRefGoogle Scholar
Edwards, M. J., Lindl, J. D., Spears, B. K., Weber, S. V., Atherton, L. J., Bleuel, D. L., Bradley, D. K., Callahan, D. A., Cerjan, C. J., Clark, D., Collins, G. W., Fair, J. E., Fortner, R. J., Glenzer, S. H., Haan, S. W., Hammel, B. A., Hamza, A. V., Hatchett, S. P., Izumi, N., Jacoby, B., Jones, O. S., Koch, J. A., Kozioziemski, B. J., Landen, O. L., Lerche, R., MacGowan, B. J., MacKinnon, A. J., Mapoles, E. R., Marinak, M. M., Moran, M., Moses, E. I., Munro, D. H., Schneider, D. H., Sepke, S. M., Shaughnessy, D. A., Springer, P. T., Tommasini, R., Bernstein, L., Stoeffl, W., Betti, R., Boehly, T. R., Sangster, T. C., Glebov, V. Y., McKenty, P. W., Regan, S. P., Edgell, D. H., Knauer, J. P., Stoeckl, C., Harding, D. R., Batha, S., Grim, G., Herrmann, H. W., Kyrala, G., Wilke, M., Wilson, D. C., Frenje, J., Petrasso, R., Moreno, K., Huang, H., Chen, K. C., Giraldez, E., Kilkenny, J. D., Mauldin, M., Hein, N., Hoppe, M., Nikroo, A. & Leeper, R. J. 2011 The experimental plan for cryogenic layered target implosions on the national ignition facility: the inertial confinement approach to fusion. Phys. Plasmas 18 (5), 051003.CrossRefGoogle Scholar
Glass, I. I. & Patterson, G. N. 1955 A theoretical and experimental study of shock-tube flows. J. Aero. Sci. 22, 73–100.CrossRefGoogle Scholar
Goncharov, V. N. 2002 Analytical model of nonlinear, single-mode, classical Rayleigh–Taylor instability at arbitrary Atwood numbers. Phys. Rev. Lett. 88, 134502.CrossRefGoogle ScholarPubMed
Grinstein, F. F., Gowhardhan, A. A. & Wachtor, A. J. 2011 Simulations of Richtmyer–Meshkov instabilities in planar shock-tube experiments. Phys. Fluids 23, 034106.CrossRefGoogle Scholar
Hahn, M., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2011 Richtmyer–Meshkov turbulent mixing arising from an inclined material interface with realistic surface perturbations and reshocked flow. Phys. Fluids 23, 046101.CrossRefGoogle Scholar
Herrmann, M., Moin, P. & Abarzhi, S. I. 2008 Nonlinear evolution of the Richtmyer–Meshkov instability. J. Fluid Mech. 612, 311–338.CrossRefGoogle Scholar
Holmes, R. L., Dimonte, G., Fryxell, B., Gittings, M. L., Grove, J. W., Schneider, M., Sharp, D. H., Velikovich, A. L., Weaver, R. P. & Zhang, Q. 1999 Richtmyer–Meshkov instability growth: experiment, simulation and theory. J. Fluid Mech. 389, 55–79.CrossRefGoogle Scholar
Huerte Ruiz de Lira, C., Velikovich, A. L. & Wouchuk, J. G. 2011 Analytical linear theory for the interaction of a planar shock wave with a two- or three-dimensional random isotropic density field. Phys. Rev. E 83, 056320.CrossRefGoogle Scholar
Jacobs, J. W. 1993 The dynamics of shock accelerated light and heavy gas cylinders. Phys. Fluids A 5, 2239–2247.CrossRefGoogle Scholar
Jacobs, J. W., Jenkins, D. G., Klein, D. L. & Benjamin, R. F. 1995 Nonlinear growth of the shock-accelerated instability of a thin fluid layer. J. Fluid Mech. 295, 23–42.CrossRefGoogle Scholar
Jacobs, J. W., Klein, D. L., Jenkins, D. G. & Benjamin, R. F. 1993 Instability growth patterns of a shock-accelerated thin fluid layer. Phys. Rev. Lett. 70, 583–586.CrossRefGoogle ScholarPubMed
Jacobs, J. W. & Krivets, V. V. 2005 Experiments on the late-time development of single-mode Richtmyer–Meshkov instability. Phys. Fluids 17, 034105.CrossRefGoogle Scholar
Jacobs, J. W. & Sheeley, J. M. 1996 Experimental study of the Richtmyer–Meshkov instability of incompressible fluids. Phys. Fluids 8, 405–415.CrossRefGoogle Scholar
Jones, M. A. & Jacobs, J. W. 1997 A membraneless experiment for the study of Richtmyer–Meshkov instability of a shock-accelerated gas interface. Phys. Fluids 9, 3078–3085.CrossRefGoogle Scholar
Keane, R. D. & Adrian, R. J. 1990 Optimization of particle image velocimeters. Part 1. Double pulsed systems. Meas. Sci. Technol. 1, 1202–1215.CrossRefGoogle Scholar
Keane, R. D. & Adrian, R. J. 1991 Optimization of particle image velocimeters. Part 2. Multiple pulsed systems. Meas. Sci. Technol. 2, 963–974.CrossRefGoogle Scholar
Kifonidis, K., Plewa, T., Sheck, L., Janka, H.-T. & Müller, E. 2006 Non-spherical core collapse supernovae. Astron. Astrophys. 453, 661–678.CrossRefGoogle Scholar
Kolev, T. V. & Rieben, R. N. 2009 A tensor artificial viscosity using finite element approach. J. Comput. Phys. 228, 8336–8366.CrossRefGoogle Scholar
Krechetnikov, R. 2009 Rayleigh–Taylor and Richtmyer–Meshkov instabilities of flat and curved interfaces. J. Fluid. Mech. 625, 387–410.CrossRefGoogle Scholar
Layzer, D. 1955 On the instability of superposed fluids in a gravitational field. Astrophys. Rev. J. 122, 1–12.CrossRefGoogle Scholar
Likhachev, O. A. & Jacobs, J. W. 2005 A vortex model for Richtmyer–Meshkov instability accounting for finite Atwood number. Phys. Fluids 17, 031704.CrossRefGoogle Scholar
Liu, B. Y. H. & Lee, K. W. 1975 An aerosol generator of high stability. Am. Ind. Hyg. Assoc. 36, 861–865.CrossRefGoogle ScholarPubMed
Lombardini, M., Hill, D. J., Pullin, D. I. & Meiron, D. I. 2011 Atwood ratio dependence of Richtmyer–Meshkov flows under reshock conditions using large-eddy simulations. J. Fluid Mech. 670, 439–480.CrossRefGoogle Scholar
Mariani, C., Vandenboomgaerde, M., Jourdan, G., Souffland, D. & Houas, L. 2008 Investigation of the Richtmyer–Meshkov instability with stereolithographed interfaces. Phys. Rev. Lett. 100, 254503.CrossRefGoogle ScholarPubMed
Matsuoka, C., Nishihara, K. & Fukuda, Y. 2003 Nonlinear evolution of an interface in the Richtmyer–Meshkov instability. Phys. Rev. E 67, 036301.CrossRefGoogle ScholarPubMed
McFarland, J. A., Greenough, J. A. & Ranjan, D. 2011 Computational parametric study of a Richtmyer–Meshkov instability for an inclined interface. Phys. Rev. E 84, 026303.CrossRefGoogle ScholarPubMed
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Izv. Akad. Nauk. SSSR Maekh. Zhidk. Gaza. 4, 151–157.Google Scholar
Meyer, K. A. & Blewett, P. J. 1972 Numerical investigation of the stability of a shock-accelerated interface between two fluids. Phys. Fluids 15, 753–759.CrossRefGoogle Scholar
Mikaelian, K. O. 2003 Explicit expressions for the evolution of single-mode Rayleigh–Taylor and Richtmyer–Meshkov instabilities at arbitrary Atwood numbers. Phys. Rev. E 67, 026319.CrossRefGoogle ScholarPubMed
Mirels, H. 1956 Attenuation in a shock-tube due to unsteady-boundary-layer action. NACA TN3278.Google Scholar
Mirels, H. & Braun, W. H. 1957 Nonuniformities in shock-tube flow due to unsteady-boundary-layer action. NACA TN4021.Google Scholar
Motl, B., Niederhaus, J., Ranjan, D., Oakley, J., Anderson, M. & Bonazza, R. 2007 Experimental studies for ICF related Richtmyer–Meshkov instabilities. Fus. Sci. Tech. 52, 1079–1083.CrossRefGoogle Scholar
Nishihara, K., Wouchuk, J. G., Matsuoka, C., Ishizaki, R. & Zhakhovsky, V. V. 2010 Richtmyer–Meshkov instability: theory of linear and nonlinear evolution. Phil. Trans. R. Soc. A 368, 1769–1807.CrossRefGoogle ScholarPubMed
Oron, D., Arazi, L., Kartoon, D., Rkanati, A., Alon, U. & Shvarts, D. 2001 Dimensionality dependence of the Rayleigh–Taylor and Richtmyer–Meshkov instability late-time scaling laws. Phys. Plasmas 8, 2108–2115.CrossRefGoogle Scholar
Peng, G., Zabusky, N. J. & Zhang, S. 2003 Vortex-accelerated secondary baroclinic vorticity deposition and late-intermediate time dynamics of a two-dimensional Richtmyer–Meshkov interface. Phys. Fluids 15, 3730–3744.CrossRefGoogle Scholar
Prasad, J. K., Rasheed, A., Kumar, S. & Sturtevant, B. 2000 The late-time development of the Richtmyer–Meshkov instability. Phys. Fluids 12, 3730–3744.CrossRefGoogle Scholar
Raffel, M., Kompenhans, J. & Willert, C. E. 1998 Particle Image Velocimetry: A Practical Guide. Springer.CrossRefGoogle Scholar
Rayleigh, Lord 1900 Investigation of the Character of the Equilibrium of an Incompressible Heavy Fluid of Variable Density. Cambridge University Press.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Math. 23, 297–319.CrossRefGoogle Scholar
Roshko, A. 1960 On flow duration in low-pressure shock tubes. Phys. Fluids 3, 835–842.CrossRefGoogle Scholar
Sadot, O., Erez, L., Alon, U., Oron, D., Levin, L. A., Erez, G., Ben-Dor, B. & Shvarts, D. 1998 Study of nonlinear evolution of single-mode and two-bubble interaction under Richtmyer–Meshkov instability. Phys. Rev. Lett. 80, 1654–1657.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory, 8th edn. Springer.CrossRefGoogle Scholar
Schilling, O., Latini, M. & Don, W. S. 2007 Physics of reshock and mixing in single-mode Richtmyer–Meshkov instability. Phys. Rev. E 76, 026319.CrossRefGoogle ScholarPubMed
Sharp, R. W. Jr & Barton, R. T. 1981 Hemp advection model. UCID-17809 Rev.1, Lawrence Livermore Laboratory.Google Scholar
Sohn, S.-I. 2011 Inviscid and viscous vortex models for Richtmyer–Meshkov instability. Fluid Dyn. Res. 43, 065506.CrossRefGoogle Scholar
Taylor, G. I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. Part 1. Proc. R. Soc. A 201, 192–196.Google Scholar
Thornber, B., Drikakis, D., Youngs, D. L. & Williams, R. J. R. 2011 Growth of a Richtmyer–Meshkov turbulent layer after reshock. Phys. Fluids 23, 095107.CrossRefGoogle Scholar
Tomkins, C., Kumar, S., Orlicz, G. & Prestridge, K. 2008 An experimental investigation of mixing mechanisms in shock-accelerated flow. J. Fluid Mech. 611, 131–150.CrossRefGoogle Scholar
von Kármán, T. 1921 Laminar and turbulent friction. Z. Angew. Math. Mech. 1, 233–252.CrossRefGoogle Scholar
Vandenboomgaerde, M., Gauthier, S. & Mügler, C 2002 Nonlinear regime of a multimode Richtmyer–Meshkov instability: a simplified perturbation theory. Phys. Fluids 14, 1111–1122.CrossRefGoogle Scholar
Vetter, M. & Sturtevant, B. 1995 Experiments on the Richtmyer–Meshkov instability of an air/ ${\mathrm{SF} }_{6} $ interface. Shock Waves 4, 247–252.CrossRefGoogle Scholar
Westerweel, J. 1993 Digital particle image velocimetry, theory and application. PhD thesis, Technische Universiteit Delft.Google Scholar
Wilkins, M. L. 1963 Calculation of elastic–plastic flow. UCRL-7322, Lawrence Radiation Laboratory.Google Scholar
Wouchuk, J. G. & Nishihara, K. 1997 Asymptotic growth in the linear Richtmyer–Meshkov instability. Phys. Plasmas 4, 1028–1038.CrossRefGoogle Scholar
Yang, J., Kubota, Y. & Zukoski, E. E. 1993 Applications of shock-induced mixing to supersonic combustion. AIAA J. 31, 854–862.CrossRefGoogle Scholar
Zhang, Q. & Sohn, S.-I. 1997a Nonlinear theory of unstable fluid mixing driven by shock wave. Phys. Fluids 9, 1106–1124.CrossRefGoogle Scholar
Zhang, Q. & Sohn, S.-I. 1997b Padé approximation to an interfacial fluid mixing problem. Appl. Math. Lett. 10, 121–127.CrossRefGoogle Scholar