1. Introduction: the many facets of liquid perforation
Rain pouring over the ocean, spray cleaning techniques in microelectronics or promising needle-free drug injection are a few of many illustrations of liquid streams (whether jets or droplet trains) interacting with a soft/fluid target. However, the fluid dynamics of this interaction can be an intricate matter, as a closer look at these examples reveals. Take rain falling over the ocean for example: as each raindrop creates a centimetre-sized transient fluid crater upon impact, it would be easy to conclude that the typical mixing length between fresh (rain) and salty (ocean) water is of the same order of magnitude. But on each impact, self-propelled and interacting vortex rings are emitted, thereby promoting mixing. As a result, the effective ocean ‘skin’ thickness exceeds the typical crater size by a factor of a hundred (Rodriguez & Mesler Reference Rodriguez and Mesler1988; Schlössel, Soloviev & Emery Reference Schlössel, Soloviev and Emery1997). Drops falling on liquid films are also routinely used in industry, typically for cleaning purposes. In the microelectronics industry, the development of next generation smartphones or electronic devices entails the manufacture of ever smaller transistor designs, up to a point where even minute nanoparticle contaminants can endanger their viability. Cleaning techniques with e.g. liquid jets or sprays are therefore mandatory but an assessment of the hydrodynamic forces at play is here critical, for they have to overcome adhesion while not damaging the fragile technology (Kondo & Ando Reference Kondo and Ando2019). Liquid jets interacting with soft tissue are also found in medicine, as innovative ‘needle-free syringes’ shooting intense and concentrated jets that can literally perforate the skin to deliver therapeutic drugs (Mitragotri Reference Mitragotri2006; Tagawa et al. Reference Tagawa, Oudalov, Ghalbzouri, Sun and Lohse2013). In these examples, the penetration depth, the cavity geometry or the stresses exerted on the target all depend on the non-trivial fluid dynamics of the liquid stream/target interaction. Now, Lee et al. (Reference Lee, Kim, Kim, Kim and Kim2021) consider the impact of a droplet train on a liquid pool – a paradigm for the previous situations. They reveal a comprehensive picture of this interaction, from early deformation to maximum penetration and uncover a previously unreported late-stage steady state deformation for the slammed interface.
To better understand the contributions of Lee et al., it may be worth connecting their work with the almost two century long research effort on the subject. Probably one of the earliest references on impact-mediated cratering is provided by Félix Hélie in his Traité de Balistique Expérimentale in Reference Hélie1884. A professor at the French Navy military school, Hélie was interested in understanding field observations of impact and craters produced by artillery. True enough, Hélie's cannonballs were not liquid and the slammed ground not really fluid either yet he and his aide Hugoniot (who would make his own career in fluid mechanics) rationalized field observations by making use of hydrodynamical arguments. Interestingly they designed an elementary model of penetration involving what we would now call an inertial drag  ${\sim }\rho U^{2}A$ exerted by the target (here
${\sim }\rho U^{2}A$ exerted by the target (here  $\rho$ denotes the target's density, and U and A the cannonball velocity and cross-section, respectively), obtained a logarithmic law for the maximal depth which we will come back to later, and further proposed that the overall crater void was formed at the expense of the projectile's initial kinetic energy (‘la force vive que possédait le projectile à son entrée’). With their pioneering contribution, Hélie and Hugoniot laid the ground for our modern understanding of penetration in soft media.
$\rho$ denotes the target's density, and U and A the cannonball velocity and cross-section, respectively), obtained a logarithmic law for the maximal depth which we will come back to later, and further proposed that the overall crater void was formed at the expense of the projectile's initial kinetic energy (‘la force vive que possédait le projectile à son entrée’). With their pioneering contribution, Hélie and Hugoniot laid the ground for our modern understanding of penetration in soft media.
It is unfortunate that yet another wartime era led Garrett Birkhoff, G.I. Taylor and collaborators to significantly advance the knowledge of liquid perforation by studying a curious – but deadly – device: the shaped-charge jet (Birkhoff et al. Reference Birkhoff, MacDougall, Pugh and Taylor1948) that powers, e.g. the US army Bazooka. Such a weapon is able to produce highly concentrated liquid metal jets travelling at several kilometres per second. On impact, the monumental pressures exerted by the shaped-charge jet greatly exceed the target's yield stress, making any armour flow as a liquid. Birkhoff et al. identified the formation mechanism of such jets and also found that the penetration depth was related to the length of the impacting jets. Interestingly, while these stretched jets increase their length during their flight, they are also prone to rupture into fragments (i.e. metal ‘drops’); whenever such a breakdown occurred, Birkhoff et al. observed a rapid deterioration of the perforation efficiency.
Jets or streams of droplets interacting with liquids have regained interest in recent years with, e.g., Bouwhuis et al. (Reference Bouwhuis, Huang, Chan, Frommhold, Ohl, Lohse, Snoeijer and van der Meer2016), who found that the observed maximum penetration depth of a droplet train into a liquid pool was captured accurately with a free surface potential flow solver, or Speirs et al. (Reference Speirs, Pan, Belden and Truscott2018), who confirmed that fragmented jets have a lower penetration depth than their continuous counterparts.
2. Overview of Lee et al.'s article: transient holes and steady punches
Lee et al. (Reference Lee, Kim, Kim, Kim and Kim2021) propose in their article an elegant experimental study of a droplet train impacting a liquid pool combined with really simple but effective models. The experiment consists in producing a liquid jet with an ingenious pressurized tank system. The jet is excited with a piezoelectric transducer at frequency  $f$ (5–725 kHz), and disintegrates into a stream of droplets with typical diameters
$f$ (5–725 kHz), and disintegrates into a stream of droplets with typical diameters  $d$ of the order of 100
$d$ of the order of 100  $\mathrm {\mu }$m and velocities
$\mathrm {\mu }$m and velocities  $U$ ranging from a few metres per second up to almost 50 m s
$U$ ranging from a few metres per second up to almost 50 m s $^{-1}$. With the working liquids used in their study (water–ethanol mixtures and glucose syrups with density
$^{-1}$. With the working liquids used in their study (water–ethanol mixtures and glucose syrups with density  $\rho$, surface tension
$\rho$, surface tension  $\sigma$ and viscosity
$\sigma$ and viscosity  $\mu$) and gravity acceleration g, the impact on the pool is characterized by the Weber
$\mu$) and gravity acceleration g, the impact on the pool is characterized by the Weber  $We = \rho U^{2} d / \sigma$, Reynolds
$We = \rho U^{2} d / \sigma$, Reynolds  $Re = \rho U d/\mu$ and Froude
$Re = \rho U d/\mu$ and Froude  $Fr = U^{2}/gd$ numbers all greatly exceeding one. Inertia is therefore the dominant mechanism here when compared with viscous, gravity or capillary effects.
$Fr = U^{2}/gd$ numbers all greatly exceeding one. Inertia is therefore the dominant mechanism here when compared with viscous, gravity or capillary effects.
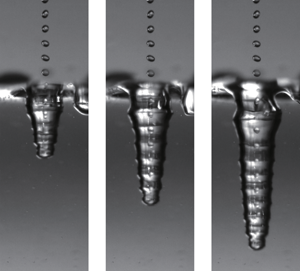
The interaction between the droplet train and the surface exhibits two sharply delimited, successive regimes. In the first moments of the interaction, the droplet train perforates the liquid as each drop impact digs the cavity deeper (figure 1a). The finger-like air cavity keeps on elongating at a constant rate up to a point where it pinches off abruptly near the surface (figure 1b). The immersed air pocket then bursts into a myriad of bubbles (figure 1c), and the interface is simply deformed or ‘punched’ due to the continuous slamming of droplets. Lee et al. obtain two main results corresponding to each of these regimes.
Figure 1. (a) In the first moments of interaction, a droplet train makes a hole of constantly increasing length in the bath. (b) The hole depth grows linearly with time up to a point of sudden pinch-off where the maximal depth is reduced to that of a steady meniscus. (c) Detail of the pinch-off event and resulting air finger bursting into a myriad of bubbles. (d) Top: control volume used to describe the interaction from an impacting drop train and the tip of the hole. Bottom: control volume around the punched interface in the steady state regime. (adapted from Lee et al.).
The first result is that cavities elongate linearly with time at a rate  $\dot H$ that can be understood with the following arguments. Consider a control volume (CV) moving with the tip of the cavity at velocity
$\dot H$ that can be understood with the following arguments. Consider a control volume (CV) moving with the tip of the cavity at velocity  $v$ (figure 1d). When an incoming drop enters the control volume at velocity
$v$ (figure 1d). When an incoming drop enters the control volume at velocity  $u$ (greater than
$u$ (greater than  $v$) and collides with the liquid, a simple momentum balance yields
$v$) and collides with the liquid, a simple momentum balance yields  $({\mathrm d}/{\mathrm dt})(m u) = \dot mu + F.$ Here
$({\mathrm d}/{\mathrm dt})(m u) = \dot mu + F.$ Here  $m$ stands for the drop mass,
$m$ stands for the drop mass,  $\dot m$ for the mass rate exiting the control volume (and therefore
$\dot m$ for the mass rate exiting the control volume (and therefore  $\dot m u$ as the rate of momentum loss) and
$\dot m u$ as the rate of momentum loss) and  $F$ is the drag exerted by the liquid surroundings and modelled as an inertial force
$F$ is the drag exerted by the liquid surroundings and modelled as an inertial force  $-\rho A v^{2}$, analogous to the force exerted on Hélie's cannonballs. From the previous balance the authors obtain the penetration
$-\rho A v^{2}$, analogous to the force exerted on Hélie's cannonballs. From the previous balance the authors obtain the penetration  $h$ resulting from a single drop impact as
$h$ resulting from a single drop impact as  $h/d=\ln (1+U\tau /d),$ where
$h/d=\ln (1+U\tau /d),$ where  $\tau$ is the time since impact, which is very close to the logarithmic penetration of cannonballs predicted by Hélie and Hugoniot (but slightly different for they also considered a Coulomb-like friction from the ground), and in excellent agreement with experimental data. Thus the mechanics of penetration results from the succession of craters dug by droplets. This iterative cratering process can be grasped by a non-dimensional elongation rate
$\tau$ is the time since impact, which is very close to the logarithmic penetration of cannonballs predicted by Hélie and Hugoniot (but slightly different for they also considered a Coulomb-like friction from the ground), and in excellent agreement with experimental data. Thus the mechanics of penetration results from the succession of craters dug by droplets. This iterative cratering process can be grasped by a non-dimensional elongation rate  $\dot H/U$ that depends solely on the Strouhal number of impact
$\dot H/U$ that depends solely on the Strouhal number of impact  $\phi = fd/U$, and is again found to capture experimental observations. Lee et al. also made use of the somewhat bold idea of Hélie (Reference Hélie1884) that the entire kinetic energy of the impacting drop was simply transmitted to the deforming substrate, and obtain the overall shape of the cavity with remarkable success.
$\phi = fd/U$, and is again found to capture experimental observations. Lee et al. also made use of the somewhat bold idea of Hélie (Reference Hélie1884) that the entire kinetic energy of the impacting drop was simply transmitted to the deforming substrate, and obtain the overall shape of the cavity with remarkable success.
The second important result obtained by Lee et al. (Reference Lee, Kim, Kim, Kim and Kim2021) is the identification of a post-pinch-off steady state regime where the interface appears to be steadily ‘punched’ in the impact zone. On using again first principles and a simple force balance ignoring gravity (figure 1d), the authors predicted the shape of the interface to be that of a capillary surface punched with a point force  $F_i$ (think of a deformed soap film). The model interface of constant (but force dependent) curvature is found again to be in remarkable agreement with experiments.
$F_i$ (think of a deformed soap film). The model interface of constant (but force dependent) curvature is found again to be in remarkable agreement with experiments.
3. Future
The beautiful agreement between experiments (we note that the whole dataset of Lee et al. (Reference Lee, Kim, Kim, Kim and Kim2021) is made publicly available through GitHub’ servers, and acknowledge this effort towards reproducible research) and simple modelling provided with the study by Lee et al. demonstrates that the essence of liquid perforation has been identified in this inertial limit. However, these results prompt several key questions that should stir the attention of the community. Much of the presented study has been devoted to an explanation of the interface shapes, but not so much of the detailed forces at play. Prior drop impact studies have revealed the highly inhomogeneous character of the impact forces both temporally and spatially (Philippi, Lagrée & Antkowiak Reference Philippi, Lagrée and Antkowiak2016). The question of the transmission and localization of stresses in the bulk liquid remains to be addressed with, e.g., acoustic sensing of forces (Bussonnière et al. Reference Bussonnière, Antkowiak, Ollivier, Baudoin and Wunenburger2020), because they are of critical importance in the context of silicon wafer cleaning for example. The topology of the flow is also unclear. The success of the static meniscus prediction is intriguing as we could have expected flow-induced free surface deformations. In the quite different context of very viscous jets impacting equally viscous baths, Lorenceau, Quéré & Eggers (Reference Lorenceau, Quéré and Eggers2004) observed the similar development of a static-like meniscus, but there the viscous jet is sheathed with a thin lubricating air layer that physically disconnect the jet flow from the meniscus. In the present experiment, there is no air layer so could a boundary layer detachment event explain the agreement between observation and a static solution? The air finger produced during impact is an intriguing object in itself: Could it be somehow stabilized? Could it reform after the interface has pinched off by varying the impact frequency for example? The capillary fragmentation of this neat air finger and the size distribution of the resulting bubble cloud are also part of the open questions of the physics of making holes in liquids.







1. Introduction: the many facets of liquid perforation
Rain pouring over the ocean, spray cleaning techniques in microelectronics or promising needle-free drug injection are a few of many illustrations of liquid streams (whether jets or droplet trains) interacting with a soft/fluid target. However, the fluid dynamics of this interaction can be an intricate matter, as a closer look at these examples reveals. Take rain falling over the ocean for example: as each raindrop creates a centimetre-sized transient fluid crater upon impact, it would be easy to conclude that the typical mixing length between fresh (rain) and salty (ocean) water is of the same order of magnitude. But on each impact, self-propelled and interacting vortex rings are emitted, thereby promoting mixing. As a result, the effective ocean ‘skin’ thickness exceeds the typical crater size by a factor of a hundred (Rodriguez & Mesler Reference Rodriguez and Mesler1988; Schlössel, Soloviev & Emery Reference Schlössel, Soloviev and Emery1997). Drops falling on liquid films are also routinely used in industry, typically for cleaning purposes. In the microelectronics industry, the development of next generation smartphones or electronic devices entails the manufacture of ever smaller transistor designs, up to a point where even minute nanoparticle contaminants can endanger their viability. Cleaning techniques with e.g. liquid jets or sprays are therefore mandatory but an assessment of the hydrodynamic forces at play is here critical, for they have to overcome adhesion while not damaging the fragile technology (Kondo & Ando Reference Kondo and Ando2019). Liquid jets interacting with soft tissue are also found in medicine, as innovative ‘needle-free syringes’ shooting intense and concentrated jets that can literally perforate the skin to deliver therapeutic drugs (Mitragotri Reference Mitragotri2006; Tagawa et al. Reference Tagawa, Oudalov, Ghalbzouri, Sun and Lohse2013). In these examples, the penetration depth, the cavity geometry or the stresses exerted on the target all depend on the non-trivial fluid dynamics of the liquid stream/target interaction. Now, Lee et al. (Reference Lee, Kim, Kim, Kim and Kim2021) consider the impact of a droplet train on a liquid pool – a paradigm for the previous situations. They reveal a comprehensive picture of this interaction, from early deformation to maximum penetration and uncover a previously unreported late-stage steady state deformation for the slammed interface.
To better understand the contributions of Lee et al., it may be worth connecting their work with the almost two century long research effort on the subject. Probably one of the earliest references on impact-mediated cratering is provided by Félix Hélie in his Traité de Balistique Expérimentale in Reference Hélie1884. A professor at the French Navy military school, Hélie was interested in understanding field observations of impact and craters produced by artillery. True enough, Hélie's cannonballs were not liquid and the slammed ground not really fluid either yet he and his aide Hugoniot (who would make his own career in fluid mechanics) rationalized field observations by making use of hydrodynamical arguments. Interestingly they designed an elementary model of penetration involving what we would now call an inertial drag ${\sim }\rho U^{2}A$ exerted by the target (here
${\sim }\rho U^{2}A$ exerted by the target (here  $\rho$ denotes the target's density, and U and A the cannonball velocity and cross-section, respectively), obtained a logarithmic law for the maximal depth which we will come back to later, and further proposed that the overall crater void was formed at the expense of the projectile's initial kinetic energy (‘la force vive que possédait le projectile à son entrée’). With their pioneering contribution, Hélie and Hugoniot laid the ground for our modern understanding of penetration in soft media.
$\rho$ denotes the target's density, and U and A the cannonball velocity and cross-section, respectively), obtained a logarithmic law for the maximal depth which we will come back to later, and further proposed that the overall crater void was formed at the expense of the projectile's initial kinetic energy (‘la force vive que possédait le projectile à son entrée’). With their pioneering contribution, Hélie and Hugoniot laid the ground for our modern understanding of penetration in soft media.
It is unfortunate that yet another wartime era led Garrett Birkhoff, G.I. Taylor and collaborators to significantly advance the knowledge of liquid perforation by studying a curious – but deadly – device: the shaped-charge jet (Birkhoff et al. Reference Birkhoff, MacDougall, Pugh and Taylor1948) that powers, e.g. the US army Bazooka. Such a weapon is able to produce highly concentrated liquid metal jets travelling at several kilometres per second. On impact, the monumental pressures exerted by the shaped-charge jet greatly exceed the target's yield stress, making any armour flow as a liquid. Birkhoff et al. identified the formation mechanism of such jets and also found that the penetration depth was related to the length of the impacting jets. Interestingly, while these stretched jets increase their length during their flight, they are also prone to rupture into fragments (i.e. metal ‘drops’); whenever such a breakdown occurred, Birkhoff et al. observed a rapid deterioration of the perforation efficiency.
Jets or streams of droplets interacting with liquids have regained interest in recent years with, e.g., Bouwhuis et al. (Reference Bouwhuis, Huang, Chan, Frommhold, Ohl, Lohse, Snoeijer and van der Meer2016), who found that the observed maximum penetration depth of a droplet train into a liquid pool was captured accurately with a free surface potential flow solver, or Speirs et al. (Reference Speirs, Pan, Belden and Truscott2018), who confirmed that fragmented jets have a lower penetration depth than their continuous counterparts.
2. Overview of Lee et al.'s article: transient holes and steady punches
Lee et al. (Reference Lee, Kim, Kim, Kim and Kim2021) propose in their article an elegant experimental study of a droplet train impacting a liquid pool combined with really simple but effective models. The experiment consists in producing a liquid jet with an ingenious pressurized tank system. The jet is excited with a piezoelectric transducer at frequency $f$ (5–725 kHz), and disintegrates into a stream of droplets with typical diameters
$f$ (5–725 kHz), and disintegrates into a stream of droplets with typical diameters  $d$ of the order of 100
$d$ of the order of 100  $\mathrm {\mu }$m and velocities
$\mathrm {\mu }$m and velocities  $U$ ranging from a few metres per second up to almost 50 m s
$U$ ranging from a few metres per second up to almost 50 m s $^{-1}$. With the working liquids used in their study (water–ethanol mixtures and glucose syrups with density
$^{-1}$. With the working liquids used in their study (water–ethanol mixtures and glucose syrups with density  $\rho$, surface tension
$\rho$, surface tension  $\sigma$ and viscosity
$\sigma$ and viscosity  $\mu$) and gravity acceleration g, the impact on the pool is characterized by the Weber
$\mu$) and gravity acceleration g, the impact on the pool is characterized by the Weber  $We = \rho U^{2} d / \sigma$, Reynolds
$We = \rho U^{2} d / \sigma$, Reynolds  $Re = \rho U d/\mu$ and Froude
$Re = \rho U d/\mu$ and Froude  $Fr = U^{2}/gd$ numbers all greatly exceeding one. Inertia is therefore the dominant mechanism here when compared with viscous, gravity or capillary effects.
$Fr = U^{2}/gd$ numbers all greatly exceeding one. Inertia is therefore the dominant mechanism here when compared with viscous, gravity or capillary effects.
The interaction between the droplet train and the surface exhibits two sharply delimited, successive regimes. In the first moments of the interaction, the droplet train perforates the liquid as each drop impact digs the cavity deeper (figure 1a). The finger-like air cavity keeps on elongating at a constant rate up to a point where it pinches off abruptly near the surface (figure 1b). The immersed air pocket then bursts into a myriad of bubbles (figure 1c), and the interface is simply deformed or ‘punched’ due to the continuous slamming of droplets. Lee et al. obtain two main results corresponding to each of these regimes.
Figure 1. (a) In the first moments of interaction, a droplet train makes a hole of constantly increasing length in the bath. (b) The hole depth grows linearly with time up to a point of sudden pinch-off where the maximal depth is reduced to that of a steady meniscus. (c) Detail of the pinch-off event and resulting air finger bursting into a myriad of bubbles. (d) Top: control volume used to describe the interaction from an impacting drop train and the tip of the hole. Bottom: control volume around the punched interface in the steady state regime. (adapted from Lee et al.).
The first result is that cavities elongate linearly with time at a rate $\dot H$ that can be understood with the following arguments. Consider a control volume (CV) moving with the tip of the cavity at velocity
$\dot H$ that can be understood with the following arguments. Consider a control volume (CV) moving with the tip of the cavity at velocity  $v$ (figure 1d). When an incoming drop enters the control volume at velocity
$v$ (figure 1d). When an incoming drop enters the control volume at velocity  $u$ (greater than
$u$ (greater than  $v$) and collides with the liquid, a simple momentum balance yields
$v$) and collides with the liquid, a simple momentum balance yields  $({\mathrm d}/{\mathrm dt})(m u) = \dot mu + F.$ Here
$({\mathrm d}/{\mathrm dt})(m u) = \dot mu + F.$ Here  $m$ stands for the drop mass,
$m$ stands for the drop mass,  $\dot m$ for the mass rate exiting the control volume (and therefore
$\dot m$ for the mass rate exiting the control volume (and therefore  $\dot m u$ as the rate of momentum loss) and
$\dot m u$ as the rate of momentum loss) and  $F$ is the drag exerted by the liquid surroundings and modelled as an inertial force
$F$ is the drag exerted by the liquid surroundings and modelled as an inertial force  $-\rho A v^{2}$, analogous to the force exerted on Hélie's cannonballs. From the previous balance the authors obtain the penetration
$-\rho A v^{2}$, analogous to the force exerted on Hélie's cannonballs. From the previous balance the authors obtain the penetration  $h$ resulting from a single drop impact as
$h$ resulting from a single drop impact as  $h/d=\ln (1+U\tau /d),$ where
$h/d=\ln (1+U\tau /d),$ where  $\tau$ is the time since impact, which is very close to the logarithmic penetration of cannonballs predicted by Hélie and Hugoniot (but slightly different for they also considered a Coulomb-like friction from the ground), and in excellent agreement with experimental data. Thus the mechanics of penetration results from the succession of craters dug by droplets. This iterative cratering process can be grasped by a non-dimensional elongation rate
$\tau$ is the time since impact, which is very close to the logarithmic penetration of cannonballs predicted by Hélie and Hugoniot (but slightly different for they also considered a Coulomb-like friction from the ground), and in excellent agreement with experimental data. Thus the mechanics of penetration results from the succession of craters dug by droplets. This iterative cratering process can be grasped by a non-dimensional elongation rate  $\dot H/U$ that depends solely on the Strouhal number of impact
$\dot H/U$ that depends solely on the Strouhal number of impact  $\phi = fd/U$, and is again found to capture experimental observations. Lee et al. also made use of the somewhat bold idea of Hélie (Reference Hélie1884) that the entire kinetic energy of the impacting drop was simply transmitted to the deforming substrate, and obtain the overall shape of the cavity with remarkable success.
$\phi = fd/U$, and is again found to capture experimental observations. Lee et al. also made use of the somewhat bold idea of Hélie (Reference Hélie1884) that the entire kinetic energy of the impacting drop was simply transmitted to the deforming substrate, and obtain the overall shape of the cavity with remarkable success.
The second important result obtained by Lee et al. (Reference Lee, Kim, Kim, Kim and Kim2021) is the identification of a post-pinch-off steady state regime where the interface appears to be steadily ‘punched’ in the impact zone. On using again first principles and a simple force balance ignoring gravity (figure 1d), the authors predicted the shape of the interface to be that of a capillary surface punched with a point force $F_i$ (think of a deformed soap film). The model interface of constant (but force dependent) curvature is found again to be in remarkable agreement with experiments.
$F_i$ (think of a deformed soap film). The model interface of constant (but force dependent) curvature is found again to be in remarkable agreement with experiments.
3. Future
The beautiful agreement between experiments (we note that the whole dataset of Lee et al. (Reference Lee, Kim, Kim, Kim and Kim2021) is made publicly available through GitHub’ servers, and acknowledge this effort towards reproducible research) and simple modelling provided with the study by Lee et al. demonstrates that the essence of liquid perforation has been identified in this inertial limit. However, these results prompt several key questions that should stir the attention of the community. Much of the presented study has been devoted to an explanation of the interface shapes, but not so much of the detailed forces at play. Prior drop impact studies have revealed the highly inhomogeneous character of the impact forces both temporally and spatially (Philippi, Lagrée & Antkowiak Reference Philippi, Lagrée and Antkowiak2016). The question of the transmission and localization of stresses in the bulk liquid remains to be addressed with, e.g., acoustic sensing of forces (Bussonnière et al. Reference Bussonnière, Antkowiak, Ollivier, Baudoin and Wunenburger2020), because they are of critical importance in the context of silicon wafer cleaning for example. The topology of the flow is also unclear. The success of the static meniscus prediction is intriguing as we could have expected flow-induced free surface deformations. In the quite different context of very viscous jets impacting equally viscous baths, Lorenceau, Quéré & Eggers (Reference Lorenceau, Quéré and Eggers2004) observed the similar development of a static-like meniscus, but there the viscous jet is sheathed with a thin lubricating air layer that physically disconnect the jet flow from the meniscus. In the present experiment, there is no air layer so could a boundary layer detachment event explain the agreement between observation and a static solution? The air finger produced during impact is an intriguing object in itself: Could it be somehow stabilized? Could it reform after the interface has pinched off by varying the impact frequency for example? The capillary fragmentation of this neat air finger and the size distribution of the resulting bubble cloud are also part of the open questions of the physics of making holes in liquids.
Declaration of interests
The author reports no conflict of interest.