Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-22T13:32:21.565Z Has data issue: false hasContentIssue false
  • English
  • Français

Localised estimation and control of linear instabilities in two-dimensional wall-bounded shear flows

Published online by Cambridge University Press:  13 July 2017

H. J. Tol Open the ORCID record for H. J. Tol [Opens in a new window] ,
M. Kotsonis ,
C. C. de Visser  and
B. Bamieh
H. J. Tol*
Affiliation:
Faculty of Aerospace Engineering, Delft University of Technology, Postbus 5058, 2600GB Delft, The Netherlands
M. Kotsonis
Affiliation:
Faculty of Aerospace Engineering, Delft University of Technology, Postbus 5058, 2600GB Delft, The Netherlands
C. C. de Visser
Affiliation:
Faculty of Aerospace Engineering, Delft University of Technology, Postbus 5058, 2600GB Delft, The Netherlands
B. Bamieh
Affiliation:
Department of Mechanical Engineering, University of California, Santa Barbara, CA 93106-5070, USA
*
†Email address for correspondence: h.j.tol@tudelft.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

A new framework is presented for estimation and control of instabilities in wall-bounded shear flows described by the linearised Navier–Stokes equations. The control design considers the use of localised actuators/sensors to account for convective instabilities in an 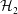${\mathcal{H}}_{2}$ optimal control framework. External sources of disturbances are assumed to enter the control domain through the inflow. A new inflow disturbance model is proposed for external excitation of the perturbation modes that contribute to transition. This model allows efficient estimation of the flow perturbations within the localised control region of a conceptually unbounded domain. The state-space discretisation of the infinite-dimensional system is explicitly obtained, which allows application of linear control theoretic tools. A reduced-order model is subsequently derived using exact balanced truncation that captures the input/output behaviour and the dominant perturbation dynamics. This model is used to design an ${\mathcal{H}}_{2}$ optimal controller to suppress the instability growth. The two-dimensional non-periodic channel flow is considered as an application case. Disturbances are generated upstream of the control domain and the resulting flow perturbations are estimated/controlled using point wall shear measurements and localised unsteady blowing and suction at the wall. The controller is able to cancel the perturbations and is robust to both unmodelled disturbances and sensor inaccuracies. For single-frequency and multiple-frequency disturbances with low sensor noise a nearly full cancellation is achieved. For stochastic forced disturbances and high sensor noise an energy reduction in perturbation wall shear stress of 96 % is shown.

JFM classification

Flow Control: Control theory Flow Control: Flow Control Flow Control: Instability control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 824 , 10 August 2017 , pp. 818 - 865
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aamo, O. M. & Krstic, M. 2002 Flow Control by Feedback. Springer.Google Scholar
Ahuja, S. & Rowley, C. W. 2010 Feedback control of unstable steady states of flow past a flat plate using reduced-order estimators. J. Fluid Mech. 645, 447–478.Google Scholar
Åkervik, E., Hoepffner, J., Ehrenstein, U. & Henningson, D. S. 2007 Optimal growth, model reduction and control in a separated boundary-layer flow using global eigenmodes. J. Fluid Mech. 579, 305–314.Google Scholar
Anderson, B. D. O. & Liu, Y. 1989 Controller reduction: concepts and approaches. IEEE Trans. Autom. Control 34, 802–812.CrossRefGoogle Scholar
Andersson, P., Berggren, M. & Henningson, D. S. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11 (1), 134–150.Google Scholar
Awanou, G. & Lai, M. J. 2004 Trivariate spline approximations of 3D Navier–Stokes equations. Maths Comput. 74 (250), 585–601.Google Scholar
Awanou, G., Lai, M. J. & Wenston, P. 2005 The multivariate spline method for scattered data fitting and numerical solutions of partial differential equations. In Wavelets and Splines (ed. Chen, G. & Lai, M. J.), pp. 24–75. Nashboro Press.Google Scholar
Bagheri, S., Åkervik, E., Brandt, L. & Henningson, D. S. 2009a Matrix-free methods for the stability and control of boundary layers. AIAA J. 47 (5), 1057–1068.Google Scholar
Bagheri, S., Brandt, L. & Henningson, D. S. 2009b Input–output analysis, model reduction and control of the flat-plate boundary layer. J. Fluid Mech. 620, 263–298.Google Scholar
Bagheri, S. & Henningson, D. S. 2011 Transition delay using control theory. Phil. Trans. R. Soc. Lond. A 369 (1940), 1365–1381.Google Scholar
Bagheri, S., Henningson, D. S., Hoepffner, J. & Schmid, P. J. 2009c Input–output analysis and control design applied to a linear model of spatially developing flows. Appl. Mech. Rev. 62 (2), 020803.CrossRefGoogle Scholar
Balas, M. J. 1979 Feedback control of linear diffusion processes. Intl J. Control 29 (3), 523–534.CrossRefGoogle Scholar
Bamieh, B., Paganini, F. & Dahleh, M. 2002 Distributed control of spatially invariant systems. IEEE Trans. Autom. Control 47 (7), 1091–1107.Google Scholar
Baramov, L., Tutty, O. R. & Rogers, E. 2004 H∞ control of nonperiodic two-dimensional channel flow. IEEE Trans. Control Syst. Technol. 12 (1), 111–122.CrossRefGoogle Scholar
Barbagallo, A., Sipp, D. & Schmid, P. J. 2009 Closed-loop control of an open cavity flow using reduced-order models. J. Fluid Mech. 641, 1–50.Google Scholar
Belson, B. A., Semeraro, O., Rowley, C. W. & Henningson, D. S. 2013 Feedback control of instabilities in the two-dimensional Blasius boundary layer: the role of sensors and actuators. Phys. Fluids 25 (5), 054106.Google Scholar
Bertolotti, F. P., Herbert, Th. & Spalart, P. R. 1992 Linear and nonlinear stability of the Blasius boundary layer. J. Fluid Mech. 242, 441–474.Google Scholar
Bewley, T. R. & Liu, S. 1998 Optimal and robust control and estimation of linear paths to transition. J. Fluid Mech. 365, 305–349.Google Scholar
Bewley, T. R., Temam, R. & Ziane, M. 2000 A general framework for robust control in fluid mechanics. Physica D 138 (3–4), 260–392.Google Scholar
de Boor, C. 1987 B-form basics. In Geometric Modeling: Algorithms and New Trends (ed. Farin, G. E.), pp. 131–148. SIAM.Google Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4 (8), 1637–1650.CrossRefGoogle Scholar
Chevalier, M., Hœpffner, J., Åkervik, E. & Henningson, D. S. 2007 Linear feedback control and estimation applied to instabilities in spatially developing boundary layers. J. Fluid Mech. 588, 163–187.CrossRefGoogle Scholar
Chevalier, M., Hœpffner, J., Bewley, T. R. & Henningson, D. S. 2006 State estimation in wall-bounded flow systems. Part 2. Turbulent flows. J. Fluid Mech. 552, 167–187.Google Scholar
Cortelezzi, L. & Speyer, J. L. 1998 Robust reduced-order controller of laminar boundary layer transitions. Phys. Rev. E 58 (2), 1906–1910.Google Scholar
Curtain, R. F. & Zwart, H. J. 1995 An Introduction to Infinite-dimensional Linear Systems Theory. Springer.Google Scholar
Dadfar, R., Semeraro, O., Hanifi, A. & Henningson, D. S. 2013 Output feedback control of Blasius flow with leading edge using plasma actuator. AIAA J. 51 (9), 2192–2207.Google Scholar
Doyle, J. C., Glover, K., Khargonekar, P. P. & Francis, B. 1989 State-space solutions to standard H 2 and H ∞ control problems. IEEE Trans. Autom. Control 34 (8), 831–847.Google Scholar
Fabbiane, N., Simon, B., Fischer, F., Grundmann, S., Bagheri, S. & Henningson, D. S. 2015 On the role of adaptivity for robust laminar flow control. J. Fluid Mech. 767, R1.Google Scholar
Farin, G. 1986 Triangular Bernstein–Bézier patches. Comput.-Aided Geom. Des. 3 (2), 83–127.CrossRefGoogle Scholar
Fattorini, H. O. 1968 Boundary control systems. SIAM J. Control 6 (3), 349–385.Google Scholar
Flinois, T. L. B. & Morgans, A. S. 2016 Feedback control of unstable flows: a direct modelling approach using the eigensystem realization algorithm. J. Fluid Mech. 793, 41–78.Google Scholar
Hœpffner, J., Chevalier, M., Bewley, T. R. & Henningson, D. S. 2005 State estimation in wall-bounded flow systems. Part 1. Perturbed laminar flows. J. Fluid Mech. 534, 263–294.Google Scholar
Högberg, M., Bewley, T. R. & Henningson, D. S. 2003a Linear feedback control and estimation of transition in plane channel flow. J. Fluid Mech. 481, 149–175.Google Scholar
Högberg, M., Bewley, T. R. & Henningson, D. S. 2003b Relaminarization of Re 𝜏 = 100 turbulence using gain scheduling and linear state-feedback control. Phys. Fluids 15 (11), 3572–3575.Google Scholar
Högberg, M. & Henningson, D. S. 2002 Linear optimal control applied to instabilities in spatially developing boundary layers. J. Fluid Mech. 470, 151–179.Google Scholar
Ilak, M. & Rowley, C. W. 2008 Modeling of transitional channel flow using balanced proper orthogonal decomposition. Phys. Fluids 20 (3), 034103.CrossRefGoogle Scholar
Illingworth, S. J., Morgans, A. S. & Rowley, C. W. 2012 Feedback control of cavity flow oscillations using simple linear models. J. Fluid Mech. 709, 223–248.Google Scholar
Jones, B. L., Heins, P. H., Kerrigan, E. C., Morrison, J. F. & Sharma, A. S. 2015 Modelling for robust feedback control of fluid flows. J. Fluid Mech. 769, 687–722.Google Scholar
Joshi, S. S., Speyer, J. L. & Kim, J. 1997 A systems theory approach to the feedback stabilization of infinitesimal and finite-amplitude disturbances in plane Poiseuille flow. J. Fluid Mech. 332, 157–184.Google Scholar
Jovanovic, M. R. & Bamieh, B. 2005 Componentwise energy amplification in channel flows. J. Fluid Mech. 534, 145–183.Google Scholar
Juang, J. N. & Pappa, R. S. 1985 An eigensystem realization algorithm for modal parameter identification and model reduction. J. Guidance Control Dyn. 8 (5), 620–627.CrossRefGoogle Scholar
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.Google Scholar
Kotsonis, M., Giepman, R., Hulshoff, S. & Veldhuis, L. 2013 Numerical study of the control of Tollmien–Schlichting waves using plasma actuators. AIAA J. 51 (10), 2353–2364.Google Scholar
Lai, M. J. & Schumaker, L. L. 2007 Spline Functions on Triangulations. Cambridge University Press.CrossRefGoogle Scholar
Lai, M. J. & Wenston, P 2004 Bivariate splines for fluid flows. Comput. Fluids 33 (8), 1047–1073.Google Scholar
Laub, A. J., Heath, M. T., Paige, C. C. & Ward, R. C. 1987 Computation of system balancing transformations and other applications of simultaneous diagonalization algorithms. IEEE Trans. Autom. Control 32 (2), 115–122.Google Scholar
Lee, K. H., Cortelezzi, L., Kim, J. & Speyer, J. 2001 Application of reduced-order controller to turbulent flows for drag reduction. Phys. Fluids 13 (5), 1321–1330.Google Scholar
Ma, Z., Ahuja, S. & Rowley, C. W. 2011 Reduced-order models for control of fluids using the eigensystem realization algorithm. Theor. Comput. Fluid Dyn. 25 (1–4), 233–247.Google Scholar
Monokrousos, A., Brandt, L., Schlatter, P. & Henningson, D. S. 2008 DNS and LES of estimation and control of transition in boundary layers subject to free-stream turbulence. Intl J. Heat Fluid Flow 29 (3), 841–855.Google Scholar
Moore, B. C. 1981 Principal component analysis in linear systems: controllability, observability, and model reduction. IEEE Trans. Autom. Control 26 (1), 17–32.Google Scholar
Noack, B. R., Afanasiev, K., Morzynski, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.Google Scholar
Pastoor, M., Henning, L., Noack, B. R., King, R. & Tadmor, G. 2008 Feedback shear layer control for bluff body drag reduction. J. Fluid Mech. 608, 161–196.Google Scholar
Rannacher, R., Turek, S. & Heywood, J. G. 1996 Artificial boundaries and flux and pressure conditions for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 22, 325–352.Google Scholar
Rowley, C. W. 2005 Model reduction for fluids, using balanced proper orthogonal decomposition. Intl J. Bifurcation Chaos 15 (03), 997–1013.Google Scholar
Samimy, M., Debiasi, M., Caraballo, E., Serrani, A., Yuan, X., Little, J. & Myatt, J. H. 2007 Feedback control of subsonic cavity flows using reduced-order models. J. Fluid Mech. 579, 315–346.Google Scholar
Saric, W. S., Reed, H. L. & Kerschen, E. J. 2002 Boundary-layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 34 (1), 291–319.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schmid, P. J. & Sipp, D. 2016 Linear control of oscillator and amplifier flows. Phys. Rev. Fluids 1, 040501.CrossRefGoogle Scholar
Semeraro, O., Bagheri, S., Brandt, L. & Henningson, D. S. 2011 Feedback control of three-dimensional optimal disturbances using reduced-order models. J. Fluid Mech. 677, 63–102.CrossRefGoogle Scholar
Semeraro, O., Bagheri, S., Brandt, L. & Henningson, D. S. 2013 Transition delay in a boundary layer flow using active control. J. Fluid Mech. 731, 288–311.Google Scholar
Sharma, A. S., Morrison, J. F., McKeon, B. J., Limebeer, D. J. N., Koberg, W. H. & Sherwin, S. J. 2011 Relaminarisation of Re 𝜏 = 100 channel flow with globally stabilising linear feedback control. Phys. Fluids 23 (12), 125105.Google Scholar
Siegel, S. G., Seidel, J., Fagley, C., Luchtenburg, D. M., Cohen, K. & McLaughlin, T. 2008 Low-dimensional modelling of a transient cylinder wake using double proper orthogonal decomposition. J. Fluid Mech. 610, 1–42.Google Scholar
Sipp, D. & Schmid, P. J. 2016 Linear closed-loop control of fluid instabilities and noise-induced perturbations: a review of approaches and tools. Appl. Mech. Rev. 68 (2), 020801.Google Scholar
Skogestad, S. & Postlethwaite, I. 2005 Multivariable Feedback Control: Analysis and Design. Wiley.Google Scholar
Tol, H. J., de Visser, C. C. & Kotsonis, M. 2016 Model reduction of parabolic PDEs using multivariate splines. Intl J. Control; published online 21 September 2016, doi:10.1080/00207179.2016.1222554.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.CrossRefGoogle ScholarPubMed
de Visser, C. C., Chu, Q. P. & Mulder, J. A. 2009 A new approach to linear regression with multivariate splines. Automatica 45 (12), 2903–2909.Google Scholar
de Visser, C. C., Chu, Q. P. & Mulder, J. A. 2011 Differential constraints for bounded recursive identification with multivariate splines. Automatica 47 (9), 2059–2066.Google Scholar
Zhou, K., Doyle, J. C. & Glover, K. 1996 Robust and Optimal Control. Prentice Hall.Google Scholar

Tol et al. supplementary movie 1

Closed-loop simulations Case A: Single frequency disturbance

Download Tol et al. supplementary movie 1(Video)
Video 8.3 MB

Tol et al. supplementary movie 2

Closed-loop simulations Case B: Multiple frequency disturbance

Download Tol et al. supplementary movie 2(Video)
Video 11.9 MB

Tol et al. supplementary movie 3

Closed-loop simulations Case C: Stochastic in-domain forcing

Download Tol et al. supplementary movie 3(Video)
Video 14.2 MB