Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-05-08T03:03:00.978Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability of monopolar vortices over isolated topography

Published online by Cambridge University Press:  20 March 2023

Jeasson F. Gonzalez Open the ORCID record for Jeasson F. Gonzalez [Opens in a new window]  and
L. Zavala Sansón Open the ORCID record for L. Zavala Sansón [Opens in a new window]
Jeasson F. Gonzalez
Affiliation:
Departamento de Oceanografía Física, CICESE, Carretera Ensenada-Tijuana 3918, 22860, Ensenada, Mexico
L. Zavala Sansón*
Affiliation:
Departamento de Oceanografía Física, CICESE, Carretera Ensenada-Tijuana 3918, 22860, Ensenada, Mexico
*
†Email address for correspondence: lzavala@cicese.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

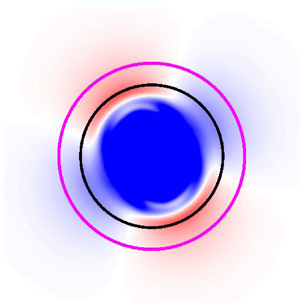
The linear instability of circular vortices over isolated topography in a homogeneous and inviscid fluid is examined for the shallow-water and quasi-geostrophic models in the $f$-plane. The eigenvalue problem associated with azimuthal disturbances is derived for arbitrary axisymmetric topographies, either submarine mountains or valleys. Amended Rayleigh and Fjørtoft theorems with topographic effects are given for barotropic instability, obtaining necessary criteria for instability when the potential vorticity gradient is zero somewhere in the domain. The onset of centrifugal instability is also discussed by deriving the Rayleigh circulation theorem with topography. The barotropic instability theorems are applied to a wide family of nonlinear, quasi-geostrophic solutions of circular vortices over axisymmetric topographic features. Flow instability depends mainly on the vortex/topography configuration, as well as on the vortex size in comparison with the width of the topography. It is found that anticyclones/mountains and cyclones/valleys may be unstable. In contrast, cyclone/mountain and anticyclone/valley configurations are stable. These statements are validated with two numerical methods. First, the generalised eigenvalue problem is solved to obtain the wavenumber of the fastest-growing perturbations. Second, the evolution of the vortices is simulated numerically to detect the development of linear perturbations. The numerical results show that for unstable vortices over narrow topographies, the fastest growth rate corresponds to mode $1$, which subsequently forms asymmetric dipolar structures. Over wide topographies, the fastest perturbations are mainly modes $1$ and $2$, depending on the topographic features.

JFM classification

Geophysical and Geological Flows: Quasi-geostrophic flows Geophysical and Geological Flows: Topographic effects Vortex Flows: Vortex instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 959 , 25 March 2023 , A23
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Carnevale, G.F. & Kloosterziel, R.C. 1994 Emergence and evolution of triangular vortices. J. Fluid Mech. 259, 305–331.CrossRefGoogle Scholar
Carnevale, G.F., Kloosterziel, R.C. & van Heijst, G.J.F. 1991 Propagation of barotropic vortices over topography in a rotating tank. J. Fluid Mech. 233, 119–139.CrossRefGoogle Scholar
Carton, X.J. & Legras, B. 1994 The life-cycle of tripoles in two-dimensional incompressible flows. J. Fluid Mech. 267, 53–82.CrossRefGoogle Scholar
Carton, X.J. & McWilliams, J.C. 1989 Barotropic and baroclinic instabilities of axisymmetric vortices in a quasigeostrophic model. In Mesoscale/Synoptic Coherent Structures in Geophysical Turbulence, Liege 1988 International Colloquium on Ocean Hydrodynamics (ed. B.M. Jamart & J.C.J. Nihoul), Elsevier Oceanographic Series, pp. 225–244. Elsevier.CrossRefGoogle Scholar
Cruz Gómez, R.C., Zavala Sansón, L. & Pinilla, M.A. 2013 Generation of isolated vortices in a rotating fluid by means of an electromagnetic method. Exp. Fluids 54, 1582-1–1582-12.CrossRefGoogle Scholar
Cushman-Roisin, B., Heil, W.H. & Nof, D. 1985 Oscillations and rotations of elliptical warm-core rings. J. Geophys. Res. Oceans 90 (C6), 11756–11764.CrossRefGoogle Scholar
Dewar, W.K. 2002 Baroclinic eddy interaction with isolated topography. J. Phys. Oceanogr. 32, 2789–2805.2.0.CO;2>CrossRefGoogle Scholar
Flierl, G.R. 1988 On the instability of geostrophic vortices. J. Fluid Mech. 197, 349–388.CrossRefGoogle Scholar
van Geffen, J.H.G.M. & Davies, P.A. 1999 Interaction of a monopolar vortex with a topographic ridge. Geophys. Astrophys. Fluid Dyn. 90 (1-2), 1–41.CrossRefGoogle Scholar
van Geffen, J.H.G.M. & Davies, P.A. 2000 A monopolar vortex encounters a north–south ridge or trough. Fluid Dyn. Res. 26, 157–179.CrossRefGoogle Scholar
Gent, P.R. & McWilliams, J.C. 1986 The instability of barotropic circular vortices. Geophys. Astrophys. Fluid Dyn. 35, 209–233.CrossRefGoogle Scholar
Gonzalez, J.F. & Zavala Sansón, L. 2021 Quasi-geostrophic vortex solutions over isolated topography. J. Fluid Mech. 915, A64.CrossRefGoogle Scholar
van Heijst, G.J.F. & Clercx, H.J.H. 2009 Laboratory modeling of geophysical vortices. Annu. Rev. Fluid Mech. 41, 143–164.CrossRefGoogle Scholar
van Heijst, G.J.F. & Kloosterziel, R.C. 1989 Tripolar vortices in a rotating fluid. Nature 338, 569–571.CrossRefGoogle Scholar
Herbette, S., Morel, Y. & Arhan, M. 2002 Erosion of a surface vortex by a seamount. J. Phys. Oceanogr. 33, 1664–1679.CrossRefGoogle Scholar
Herbette, S., Morel, Y. & Arhan, M. 2005 Erosion of a surface vortex by a seamount on the $\beta$ plane. J. Phys. Oceanogr. 35, 2012–2030.CrossRefGoogle Scholar
Kamenkovich, V.M., Leonov, Y.P., Nechaev, D.A., Byrne, D.A. & Gordon, A.L. 1996 On the influence of bottom topography on the Agulhas eddy. J. Phys. Oceanogr. 26, 892–912.2.0.CO;2>CrossRefGoogle Scholar
Kloosterziel, R.C. 1990 Barotropic vortices in a rotating fluid. PhD thesis, University of Utrecht, The Netherlands.Google Scholar
Kloosterziel, R.C. & van Heijst, G.J.F. 1991 An experimental study of unstable barotropic vortices in a rotating fluid. J. Fluid Mech. 223, 1–24.CrossRefGoogle Scholar
Kloosterziel, R.C. & van Heijst, G.J.F. 1992 The evolution of stable barotropic vortices in a rotating free-surface fluid. J. Fluid Mech. 239, 607–629.CrossRefGoogle Scholar
Nycander, J. & Lacasce, J. 2004 Stable and unstable vortices attached to seamounts. J. Fluid Mech. 507, 71–94.CrossRefGoogle Scholar
Orlandi, P. & Carnevale, G.F. 1999 Evolution of isolated vortices in a rotating fluid of finite depth. J. Fluid Mech. 381, 239–269.CrossRefGoogle Scholar
Orszag, S.A. 1971 Accurate solution of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 689–703.CrossRefGoogle Scholar
Rabinovich, M., Kizner, Z. & Flierl, G. 2018 Bottom-topography effect on the instability of flows around a circular island. J. Fluid Mech. 856, 202–227.CrossRefGoogle Scholar
Rabinovich, M., Kizner, Z. & Flierl, G. 2019 Barotropic annular flows, vortices and waves on a beta cone. J. Fluid Mech. 875, 225–253.CrossRefGoogle Scholar
Richardson, P. & Tychensky, A. 1998 Meddy trajectories in the Canary Basin measured during the SEMAPHORE experiment, 1993–1995. J. Geophys. Res. 103C, 25029–25045.CrossRefGoogle Scholar
Schouten, M.W., de Ruijter, W.P.M., van Leeuwen, P.J. & Lutjeharms, J.R.E. 2000 Translation, decay and splitting of Agulhas rings in the southeastern Atlantic Ocean. J. Geophys. Res.: Oceans 105 (C9), 21913–21925.CrossRefGoogle Scholar
Shapiro, G., Meschanov, S. & Emelianov, M. 1995 Mediterranean lens ‘Irving’ after its collision with seamounts. Ocean Acta 18, 309–318.Google Scholar
Solodoch, A., Stewart, A.L. & McWilliams, J.C. 2021 Formation of anticyclones above topographic depressions. J. Phys. Oceanogr. 51, 207–228.CrossRefGoogle Scholar
Stern, M.E. 1975 Minimal properties of planetary eddies. J. Mar. Res. 33, 1–13.Google Scholar
Sutyrin, G., Herbette, S. & Carton, X. 2011 Deformation and splitting of baroclinic eddies encountering a tall seamount. Geophys. Astrophys. Fluid Dyn. 105, 478–505.CrossRefGoogle Scholar
Trefethen, L.N. 2000 Spectral Methods in Matlab. SIAM.CrossRefGoogle Scholar
Trieling, R.R., van Heijst, G.J.F. & Kizner, Z. 2010 Laboratory experiments on multipolar vortices in a rotating fluid. Phys. Fluids 22, 1–12.CrossRefGoogle Scholar
Vallis, G.K. 2017 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Viúdez, A. 2019 a Azimuthal mode solutions of two-dimensional Euler flows and the Chaplygin–Lamb dipole. J. Fluid Mech. 859, 1–12.CrossRefGoogle Scholar
Viúdez, A. 2019 b Exact solutions of asymmetric baroclinic quasi-geostrophic dipoles with distributed potential vorticity. J. Fluid Mech. 868, 1–13.CrossRefGoogle Scholar
Yuhong, S. 1998 Collocation spectral methods in the solution of Poisson equation. PhD thesis, The University of British Columbia, Vancouver, BC.Google Scholar
Zavala Sansón, L. 2002 Vortex–ridge interaction in a rotating fluid. Dyn. Atmos. Oceans 35, 299–325.CrossRefGoogle Scholar
Zavala Sansón, L., Barbosa Aguiar, A.C. & van Heijst, G.J.F. 2012 Horizontal and vertical motions of barotropic vortices over a submarine mountain. J. Fluid Mech. 695, 173–198.CrossRefGoogle Scholar
Zavala Sansón, L. & Gonzalez, J.F. 2021 Travelling vortices over mountains and the long-term structure of the residual flow. J. Fluid Mech. 922, A33.CrossRefGoogle Scholar
Zavala Sansón, L. & van Heijst, G.J.F. 2002 Ekman effects in a rotating flow over bottom topography. J. Fluid Mech. 471, 239–255.CrossRefGoogle Scholar
Zavala Sansón, L. & van Heijst, G.J.F. 2014 Laboratory experiments on flows over bottom topography. In Modeling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments and Numerical Simulations (ed. T. von Larcher & P.D. Williams), pp. 139–158. John Wiley & Sons.CrossRefGoogle Scholar
Zhao, B., Chieusse-Gérard, E. & Flierl, G. 2019 Influence of bottom topography on vortex stability. J. Phys. Oceanogr. 49, 3199–3219.CrossRefGoogle Scholar

Gonzalez and Zavala Sansón Supplementary Movie 1

Numerically calculated vorticity distribution of an anticyclone over a wide mountain. A wave number 2 instability is developed at the end of the simulation. The vortex core (mountain) is bounded by the black (magenta) circumference.
Download Gonzalez and Zavala Sansón Supplementary Movie 1(Video)
Video 10.4 MB

Gonzalez and Zavala Sansón Supplementary Movie 2

Numerically calculated vorticity distribution of a stable cyclone over a narrow mountain. The vortex core (mountain) is bounded by the black (magenta) circumference.
Download Gonzalez and Zavala Sansón Supplementary Movie 2(Video)
Video 8.2 MB