Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-25T04:36:29.510Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability analysis of cylindrical Rayleigh–Bénard convection

Published online by Cambridge University Press:  13 September 2012

Bo-Fu Wang ,
Dong-Jun Ma ,
Cheng Chen  and
De-Jun Sun
Bo-Fu Wang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
Dong-Jun Ma
Affiliation:
School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
Cheng Chen
Affiliation:
Low Speed Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang, Sichuan 622762, China
De-Jun Sun*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
*
†Email address for correspondence: dsun@ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

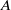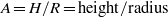The instabilities and transitions of flow in a vertical cylindrical cavity with heated bottom, cooled top and insulated sidewall are investigated by linear stability analysis. The stability boundaries for the axisymmetric flow are derived for Prandtl numbers from 0.02 to 1, for aspect ratio () equal to 1, 0.9, 0.8, 0.7, respectively. We found that there still exists stable non-trivial axisymmetric flow beyond the second bifurcation in certain ranges of Prandtl number for 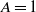, 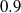and 0.8, excluding the 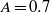case. The finding for 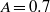is that very frequent changes of critical mode (azimuthal Fourier mode) of the second bifurcation occur when the Prandtl number is changed, where five kinds of steady modes 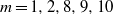and three kinds of oscillatory modes 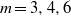are presented. These multiple modes indicate different flow structures triggered at the transitions. The instability mechanism of the flow is explained by kinetic energy transfer analysis, which shows that the radial or axial shear of base flow combined with buoyancy mechanism leads to the instability results.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Convection: Buoyancy-driven instability Convection: Convection in cavities
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 27 - 39
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bodenschatz, E., Pesch, W. & Ahlers, G 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.CrossRefGoogle Scholar
2. Borońska, K. & Tuckerman, L. S. 2006 Standing and travelling waves in cylindrical Rayleigh–Bénard convection. J. Fluid Mech. 559, 279–298.CrossRefGoogle Scholar
3. Borońska, K. & Tuckerman, L. S. 2010a Extreme multiplicity in cylindrical Rayleigh–Bénard convection. Part 1. Time-dependence and oscillations. Phys. Rev. E 81, 036320.CrossRefGoogle Scholar
4. Borońska, K. & Tuckerman, L. S. 2010b Extreme multiplicity in cylindrical Rayleigh–Bénard convection. Part 2. Bifurcation diagram and symmetry classification. Phys. Rev. E 81, 036321.CrossRefGoogle Scholar
5. Buell, J. C. & Catton, I. 1983 The effect of wall conduction on the stability of a fluid in a right circular cylinder heated from below. Trans. ASME: J. Heat Transfer 105, 255–260.CrossRefGoogle Scholar
6. Charlson, G. S. & Sani, R. L. 1970 Thermoconvective instability in a bounded cylindrical fluid layer. Intl J. Heat Mass Transfer 13, 1479–1496.CrossRefGoogle Scholar
7. Charlson, G. S. & Sani, R. L. 1971 On thermoconvective instability in a bounded cylindrical fluid layer. Intl J. Heat Mass Transfer 14, 2157–2160.CrossRefGoogle Scholar
8. Charlson, G. S. & Sani, R. L. 1975 Finite amplitude axisymmetric thermoconvective flows in a bounded cylindrical layer of fluid. J. Fluid Mech. 71, 209–229.CrossRefGoogle Scholar
9. Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65, 851–1112.CrossRefGoogle Scholar
10. Gelfgat, A. Y., Bar-Yoseph, P. Z. & Solan, A. 2000 Axisymmetry breaking instabilities of natural convection in a vertical bridgman growth configuration. J. Cryst. Growth 220, 316–325.CrossRefGoogle Scholar
11. Hardin, G. R. & Sani, R. L. 1993 Buoyancy-driven instability in a vertical cylinder: binary fluids with Soret effect. Part 2. Weakly nonlinear solutions. Intl J. Numer. Meth. Fluids 17 (9), 755–786.CrossRefGoogle Scholar
12. Hért, F., Hufschmid, R., Scheel, J. & Ahlers, G. 2010 Onset of Rayleigh–Bénard convection in cylindrical containers. Phys. Rev. E 81, 046318.CrossRefGoogle Scholar
13. Hof, B., Lucas, P. G. L. & Mullin, T. 1999 Flow state multiplicity in convection. Phys. Fluids 11 (10), 2815–2817.CrossRefGoogle Scholar
14. Hugues, S. & Randriamampianina, A. 1998 An improved projection scheme applied to pseudospectral methods for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 28, 501–521.3.0.CO;2-S>CrossRefGoogle Scholar
15. Knoll, D. A. & Keyes, D. E. 2004 Jacobian-free Newton–Krylov methods: a survey of approaches and applications. J. Comput. Phys. 193, 357–397.CrossRefGoogle Scholar
16. Lehoucq, R. B., Sorensen, D. C. & Yang, C.  (Eds) 1998 ARPACK Users Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.CrossRefGoogle Scholar
17. Leong, S. S. 2002 Numerical study of Rayleigh–Bénard convection in a cylinder. Numer. Heat Transfer A 41, 673–683.CrossRefGoogle Scholar
18. Ma, D. J., Henry, D. & Ben Hadid, H. 2005 Three-dimensional numerical study of natural convection in vertical cylinders partially heated from the side. Phys. Fluids 17, 124101.CrossRefGoogle Scholar
19. Ma, D. J., Sun, D. J. & Yin, X. Y. 2006 Multiplicity of steady states in cylindrical Rayleigh–Bénard convection. Phys. Rev. E 74, 037302.CrossRefGoogle ScholarPubMed
20. Müller, G., Neumann, G. & Weber, W. 1984 Natural convection in vertical Bridgman configurations. J. Cryst. Growth 70, 78–93.CrossRefGoogle Scholar
21. Neumann, G. 1990 Three-dimensional numerical simulation of buoyancy-driven convection in vertical cylinders heated from below. J. Fluid Mech. 214, 559–578.CrossRefGoogle Scholar
22. Rosenblat, S. 1982 Thermal convection in a vertical circular cylinder. J. Fluid Mech. 122, 395–410.CrossRefGoogle Scholar
23. Rüdiger, S. & Feudel, F. 2000 Pattern formation in Rayleigh–Bénard convection in a cylindrical container. Phys. Rev. E 62, 4927–4931.CrossRefGoogle Scholar
24. Stork, K. & Müller, U. 1975 Convection in boxes: an experimental investigation in vertical cylinders and annuli. J. Fluid Mech. 71, 231–240.CrossRefGoogle Scholar
25. Touihri, R., Ben Hadid, H. & Henry, D. 1999 On the onset of convective instabilities in cylindrical cavities heated from below. Part 1. Pure thermal case. Phys. Fluids 11, 2078–2088.CrossRefGoogle Scholar
26. Tuckerman, L. S. & Barkley, D. 2000 Bifurcation analysis for time steppers. In Numerical Methods for Bifurcation Problems and Large-Scale Dynamical Systems (ed. Doedel, E. & Tuckerman, L. S. ), vol. 119, pp. 453–466. Springer.CrossRefGoogle Scholar
27. Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for the three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123, 402–414.CrossRefGoogle Scholar
28. van der Vorst, H. A. 1992 BI-CGSTAB: a fast and smoothly converging variant of BI-CG for the solution of nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 13, 631–644.CrossRefGoogle Scholar
29. Wanschura, M., Kuhlmann, H. C. & Rath, H. J. 1996 Three-dimensional instability of axisymmetric buoyant convection in cylinders heated from below. J. Fluid Mech. 326, 399–415.CrossRefGoogle Scholar