Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-05-14T17:21:43.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Kinematics and wake of freely falling cylinders at moderate Reynolds numbers

Published online by Cambridge University Press:  05 March 2019

Clément Toupoint ,
Patricia Ern Open the ORCID record for Patricia Ern [Opens in a new window]  and
Véronique Roig
Clément Toupoint
Affiliation:
IFP Energies Nouvelles, Rond-point de l’échangeur de Solaize, BP 3, 69360 Solaize, France Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, 31400 Toulouse, France
Patricia Ern*
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, 31400 Toulouse, France
Véronique Roig
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, 31400 Toulouse, France
*
†Email address for correspondence: ern@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigated experimentally the motion of elongated finite-length cylinders (length 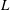$L$, diameter 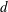$d$) freely falling under the effect of buoyancy in a low-viscosity fluid otherwise at rest. For cylinders with densities 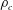$\unicode[STIX]{x1D70C}_{c}$ close to the density 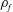$\unicode[STIX]{x1D70C}_{f}$ of the fluid (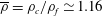$\overline{\unicode[STIX]{x1D70C}}=\unicode[STIX]{x1D70C}_{c}/\unicode[STIX]{x1D70C}_{f}\simeq 1.16$), we explored the effect of the body volume by varying the Archimedes number 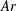$Ar$ (based on the body equivalent diameter) between 200 and 1100, as well as the effect of their length-to-diameter ratios 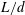$L/d$ ranging from 2 to 20. A shadowgraphy technique involving two cameras mounted on a travelling cart was used to track the cylinders along their fall over a distance longer than 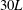$30L$. A dedicated image processing algorithm was further implemented to properly reconstruct the position and orientation of the cylinders in the three-dimensional space. In the range of parameters explored, we identified three main types of paths, matching regimes known to exist for three-dimensional bodies (short-length cylinders, disks and spheres). Two of these are stationary, namely, the rectilinear motion and the large-amplitude oscillatory motion (also referred to as fluttering or zigzag motion), and their characterization is the focus of the present paper. Furthermore, in the transitional region between these two regimes, we observed irregular low-amplitude oscillatory motions, that may be assimilated to the A-regimes or quasi-vertical regimes of the literature. Flow visualization using dye released from the bodies uncovered the existence of different types of vortex shedding in the wake of the cylinders, according to the style of path. The detailed analysis of the body kinematics in the fluttering regime brought to light a series of remarkable properties. In particular, when normalized with the characteristic velocity scale $u_{0}=\sqrt{(\overline{\unicode[STIX]{x1D70C}}-1)gd}$ and the characteristic length scale 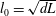$l_{0}=\sqrt{dL}$, the mean vertical velocity 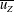$\overline{u_{Z}}$ and the frequency 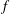$f$ of the oscillations become almost independent of 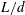$L/d$ and 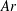$Ar$. The use of the length scale 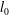$l_{0}$ and of the gravitational velocity scale to build the Strouhal number 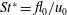$St^{\ast }=fl_{0}/u_{0}$ allowed us to generalize to short (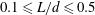$0.1\leqslant L/d\leqslant 0.5$) and elongated cylinders (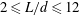$2\leqslant L/d\leqslant 12$), the result 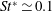$St^{\ast }\simeq 0.1$. An interpretation of 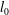$l_{0}$ as a characteristic length scale associated with the oscillatory recirculation thickness generated near the body ends is proposed. In addition, the rotation rate of the cylinders scales with 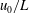$u_{0}/L$, for all 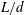$L/d$ and 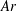$Ar$ investigated. Furthermore, the phase difference between the oscillations of the velocity component $u$ along the cylinder axis and of the inclination angle 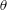$\unicode[STIX]{x1D703}$ of the cylinder is approximately constant, whatever the elongation ratio 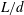$L/d$ and the Archimedes number 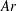$Ar$.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 82 - 111
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, A., Pesavento, U. & Wang, Z. J. 2005a Analysis of transitions between fluttering, tumbling and steady descent of falling cards. J. Fluid Mech. 541, 91–104.10.1017/S0022112005005847Google Scholar
Andersen, A., Pesavento, U. & Wang, Z. J. 2005b Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 541, 65–90.10.1017/S002211200500594XGoogle Scholar
Auguste, F. & Magnaudet, J. 2018 Path oscillations and enhanced drag of light rising spheres. J. Fluid Mech. 841, 228–266.10.1017/jfm.2018.100Google Scholar
Auguste, F., Magnaudet, J. & Fabre, D. 2013 Falling styles of disks. J. Fluid Mech. 719, 388–405.10.1017/jfm.2012.602Google Scholar
Belmonte, A., Eisenberg, H. & Moses, E. 1998 From flutter to tumble: inertial drag and Froude similarity in falling paper. Phys. Rev. Lett. 81 (2), 345–348.10.1103/PhysRevLett.81.345Google Scholar
Chow, A. C. & Adams, E. E. 2011 Prediction of drag coefficient and secondary motion of free-falling rigid cylindrical particles with and without curvature at moderate Reynolds number. J. Hydraul. Engng 137 (11), 1406–1414.10.1061/(ASCE)HY.1943-7900.0000437Google Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2013 Numerical simulation of the dynamics of freely falling discs. Phys. Fluids 25, 044102.10.1063/1.4799179Google Scholar
Dauchy, C., Dušek, J. & Fraunié, P. 1997 Primary and secondary instabilities in the wake of a cylinder with free ends. J. Fluid Mech. 332, 295–339.10.1017/S0022112096004041Google Scholar
Doignon, C. & de Mathelin, M. 2007 A degenerate conic-based method for a direct fitting and 3-D pose of cylinders with a single perspective view. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, pp. 4220–4225. IEEE.10.1109/ROBOT.2007.364128Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.10.1146/annurev-fluid-120710-101250Google Scholar
Fernandes, P. C., Ern, P., Risso, F. & Magnaudet, J. 2008 Dynamics of axisymmetric bodies rising along a zigzag path. J. Fluid Mech. 606, 209–223.10.1017/S0022112008001663Google Scholar
Fernandes, P. C., Risso, F., Ern, P. & Magnaudet, J. 2007 Oscillatory motion and wake instability of freely rising axisymmetric bodies. J. Fluid Mech. 573, 479–502.10.1017/S0022112006003685Google Scholar
Gioria, R. S., Meneghini, J. R., Aranha, J. A. P., Barbeiro, I. C. & Carmo, B. S. 2011 Effect of the domain spanwise periodic length on the flow around a circular cylinder. J. Fluids Struct. 27 (5), 792–797.10.1016/j.jfluidstructs.2011.03.007Google Scholar
Horowitz, M. & Williamson, C. H. K. 2006 Dynamics of a rising and falling cylinder. J. Fluids Struct. 22, 837–843.10.1016/j.jfluidstructs.2006.04.012Google Scholar
Horowitz, M. & Williamson, C. H. K. 2010 Vortex-induced vibration of a rising and falling cylinder. J. Fluid Mech. 662, 352–383.10.1017/S0022112010003265Google Scholar
Huang, J. B., Chen, Z. & Chia, T. L. 1996 Pose determination of a cylinder using reprojection transformation. Pattern Recogn. Lett. 17 (10), 1089–1099.10.1016/0167-8655(96)00061-XGoogle Scholar
Inoue, O. & Sakuragi, A. 2008 Vortex shedding from a circular cylinder of finite length at low Reynolds numbers. Phys. Fluids 20 (3), 033601.10.1063/1.2844875Google Scholar
Jayaweera, K. O. L. F. & Mason, B. J. 1965 The behaviour of freely falling cylinders and cones in a viscous fluid. J. Fluid Mech. 22 (4), 709–720.10.1017/S002211206500109XGoogle Scholar
Lamb, H. 1993 Hydrodynamics. Cambridge University Press.Google Scholar
Marchildon, E. K., Clamen, A. & Gauvin, W. H. 1964 Drag and oscillatory motion of freely falling cylindrical particles. Can. J. Chem. Engng 42 (4), 178–182.10.1002/cjce.5450420410Google Scholar
Mathai, V., Zhu, X., Sun, C. & Lohse, D. 2017 Mass and moment of inertia govern the transition in the dynamics and wakes of freely rising and falling cylinders. Phys. Rev. Lett. 119, 054501.10.1103/PhysRevLett.119.054501Google Scholar
Namkoong, K., Yoo, J. Y. & Choi, H. G. 2008 Numerical analysis of two-dimensional motion of a freely falling circular cylinder in an infinite fluid. J. Fluid Mech. 604, 33–54.10.1017/S0022112008001304Google Scholar
Navab, N. & Appel, M. 2006 Canonical representation and multi-view geometry of cylinders. Intl J. Comput. Vis. 70 (2), 133–149.10.1007/s11263-006-7935-4Google Scholar
Provansal, M., Schouveiler, L. & Leweke, T. 2004 From the double vortex street behind a cylinder to the wake of a sphere. Eur. J. Mech. (B/Fluids) 23, 65.10.1016/j.euromechflu.2003.09.007Google Scholar
Qu, L., Norberg, C., Davidson, L., Peng, S.-H. & Wang, F. 2013 Quantitative numerical analysis of flow past a circular cylinder at Reynolds number between 50 and 200. J. Fluids Struct. 39, 347–370.10.1016/j.jfluidstructs.2013.02.007Google Scholar
Romero-Gomez, P. & Richmond, M. C. 2016 Numerical simulation of circular cylinders in free-fall. J. Fluids Struct. 61, 154–167.10.1016/j.jfluidstructs.2015.11.010Google Scholar
Schouveiler, L. & Provansal, M. 2001 Periodic wakes of low aspect ratio cylinders with free hemispherical ends. J. Fluids Struct. 15, 565.10.1006/jfls.2000.0351Google Scholar
Shiu, Y. C. & Huang, C. 1993 Pose determination of circular cylinders using elliptical and side projections. In IEEE 1991 International Conference on Systems Engineering, pp. 265–268. IEEE.Google Scholar
Tchoufag, J., Fabre, D. & Magnaudet, J. 2014 Global linear stability analysis of the wake and path of buoyancy-driven disks and thin cylinders. J. Fluid Mech. 740, 278–311.10.1017/jfm.2013.642Google Scholar
Vakil, A. & Green, S. I. 2009 Drag and lift coefficients of inclined finite circular cylinders at moderate Reynolds numbers. Comput. Fluids 38, 1771–1781.10.1016/j.compfluid.2009.03.006Google Scholar
Williamson, C. H. K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.10.1017/S0022112089002429Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.10.1146/annurev.fl.28.010196.002401Google Scholar
Williamson, C. H. K. & Brown, G. L. 1998 A series in 1/√Re to represent the Strouhal–Reynolds number relationship of the cylinder wake. J. Fluids Struct. 12 (8), 1073–1085.10.1006/jfls.1998.0184Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.10.1146/annurev.fluid.36.050802.122128Google Scholar