Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-06-21T15:44:49.209Z Has data issue: false hasContentIssue false
  • English
  • Français

A kind of Lagrangian chaotic property of the Arnold–Beltrami–Childress flow

Published online by Cambridge University Press:  31 March 2023

Shijie Qin Open the ORCID record for Shijie Qin [Opens in a new window]  and
Shijun Liao Open the ORCID record for Shijun Liao [Opens in a new window]
Shijie Qin
Affiliation:
Center of Marine Numerical Experiment, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Shijun Liao*
Affiliation:
Center of Marine Numerical Experiment, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China State Key Laboratory of Ocean Engineering, Shanghai 200240, PR China School of Hydraulic Electric Engineering, Qinghai University, Xinning 810018, PR China
*
†Email address for correspondence: sjliao@sjtu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

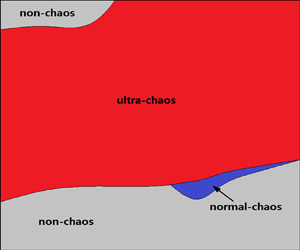
Three-dimensional steady-state Arnold–Beltrami–Childress (ABC) flow has a chaotic Lagrangian structure, and also satisfies the Navier–Stokes (NS) equations with an external force per unit mass. It is well known that, although trajectories of a chaotic system have sensitive dependence on initial conditions, i.e. the famous ‘butterfly effect’, their statistical properties are often insensitive to small disturbances. This kind of chaos (such as governed by the Lorenz equations) is called normal-chaos. However, a new concept, i.e. ultra-chaos, has been reported recently, whose statistics are unstable to tiny disturbances. Thus, ultra-chaos represents higher disorder than normal chaos. In this paper, we illustrate that ultra-chaos widely exists in Lagrangian trajectories of fluid particles in steady-state ABC flow. Moreover, solving the NS equation when $Re=50$ with the ABC flow plus a very small disturbance as the initial condition, it is found that trajectories of nearly all fluid particles become ultra-chaotic when the transition from laminar to turbulence occurs. These numerical experiments and facts highly suggest that ultra-chaos should have a relationship with turbulence. This paper identifies differences between ultra-chaos and sensitivity of statistics to parameters. Possible relationships between ultra-chaos and the Poincaré section, ultra-chaos and ergodicity/non-ergodicity, etc., are discussed. The concept of ultra-chaos opens a new perspective of chaos, the Poincaré section, ergodicity/non-ergodicity, turbulence and their inter-relationships.

JFM classification

Nonlinear Dynamical Systems: Chaos
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 960 , 10 April 2023 , A15
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnold, V.I. 1965 Sur la topologie des écoulements stationnaires des fluides parfaits. C. R. Acad. Sci. Paris 261, 17–20.Google Scholar
Ashwin, P., Wieczorek, S., Vitolo, R. & Cox, P. 2012 Tipping points in open systems: bifurcation, noise-induced and rate-dependent examples in the climate system. Phil. Trans. R. Soc. Lond. A 370 (1962), 1166–1184.Google ScholarPubMed
Birkhoff, G.D. 1931 Proof of the ergodic theorem. Proc. Natl Acad. Sci. USA 17 (12), 656–660.CrossRefGoogle ScholarPubMed
Blazevski, D. & Haller, G. 2014 Hyperbolic and elliptic transport barriers in three-dimensional unsteady flows. Physica D 273, 46–62.CrossRefGoogle Scholar
Broer, H., Simó, C. & Vitolo, R. 2002 Bifurcations and strange attractors in the Lorenz-84 climate model with seasonal forcing. Nonlinearity 15 (4), 1205.CrossRefGoogle Scholar
Childress, S. 1970 New solutions of the kinematic dynamo problem. J. Maths Phys. 11 (10), 3063–3076.CrossRefGoogle Scholar
Crane, L. 2017 Infamous three-body problem has over a thousand new solutions. New Sci. Available at: https://www.newscientist.com/article/2148074-infamous-three-body-problem-has-over-a-thousand-new-solutions/.Google Scholar
Didov, A.A. & Uleysky, M.Yu. 2018 a Analysis of stationary points and their bifurcations in the ABC-flow. Appl. Maths Comput. 330, 56–64.CrossRefGoogle Scholar
Didov, A.A. & Uleysky, M.Yu. 2018 b Nonlinear resonances in the ABC-flow. Chaos 28 (1), 013123.CrossRefGoogle ScholarPubMed
Dombre, T., Frisch, U., Greene, J.M., Hénon, M., Mehr, A. & Soward, A.M. 1986 Chaotic streamlines in the ABC flows. J. Fluid Mech. 167, 353–391.CrossRefGoogle Scholar
Finn, J.M. & Ott, E. 1988 Chaotic flows and fast magnetic dynamos. Phys. Fluids 31 (10), 2992–3011.CrossRefGoogle Scholar
Galloway, D. & Frisch, U. 1986 Dynamo action in a family of flows with chaotic streamlines. Geophys. Astrophys. Fluid Dyn. 36 (1), 53–83.CrossRefGoogle Scholar
Galloway, D. & Frisch, U. 1987 A note on the stability of a family of space-periodic Beltrami flows. J. Fluid Mech. 180, 557–564.CrossRefGoogle Scholar
Gao, S., Tao, L., Tian, X. & Yang, J. 2018 Flow around an inclined circular disk. J. Fluid Mech. 851, 687–714.CrossRefGoogle Scholar
Hu, T. & Liao, S. 2020 On the risks of using double precision in numerical simulations of spatio-temporal chaos. J. Comput. Phys. 418, 109629.CrossRefGoogle Scholar
Kuznetsov, L. & Zaslavsky, G.M. 2000 Passive particle transport in three-vortex flow. Phys. Rev. E 61 (4), 3777–3792.CrossRefGoogle ScholarPubMed
Lee, W.-K., Borthwick, A.G.L. & Taylor, P.H. 2014 Wind-induced chaotic mixing in a two-layer density-stratified shallow flow. J. Hydraul. Res. 52 (2), 219–227.CrossRefGoogle Scholar
Li, T.Y. & Yorke, J.A. 1975 Period three implies chaos. Am. Math. Mon. 82 (10), 985–992.CrossRefGoogle Scholar
Li, X., Jing, Y. & Liao, S. 2018 Over a thousand new periodic orbits of a planar three-body system with unequal masses. Publ. Astron. Soc. Japan 70 (4), 64.CrossRefGoogle Scholar
Li, X. & Liao, S. 2017 More than six hundred new families of Newtonian periodic planar collisionless three-body orbits. Sci. China Phys. Mech. 60 (12), 129511.CrossRefGoogle Scholar
Li, X. & Liao, S. 2019 Collisionless periodic orbits in the free-fall three-body problem. New Astron. 70, 22–26.CrossRefGoogle Scholar
Li, Y.C., Ho, R.D.J.G., Berera, A. & Feng, Z.C. 2020 Superfast amplification and superfast nonlinear saturation of perturbations as a mechanism of turbulence. J. Fluid Mech. 904, A27.CrossRefGoogle Scholar
Liao, S. 2009 On the reliability of computed chaotic solutions of non-linear differential equations. Tellus A 61 (4), 550–564.CrossRefGoogle Scholar
Liao, S. 2013 On the numerical simulation of propagation of micro-level inherent uncertainty for chaotic dynamic systems. Chaos, Solitons Fractals 47, 1–12.CrossRefGoogle Scholar
Liao, S. 2014 Physical limit of prediction for chaotic motion of three-body problem. Commun. Nonlinear Sci. Numer. Simul. 19 (3), 601–616.CrossRefGoogle Scholar
Liao, S.J. 2017 On the clean numerical simulation (CNS) of chaotic dynamic systems. J. Hydrodyn. 29 (5), 729–747.CrossRefGoogle Scholar
Liao, S. & Qin, S. 2022 Ultra-chaos: an insurmountable objective obstacle of reproducibility and replication. Adv. Appl. Maths Mech. 14 (4), 799–815.CrossRefGoogle Scholar
Liao, S. & Wang, P. 2014 On the mathematically reliable long-term simulation of chaotic solutions of Lorenz equation in the interval $[0,10\,000]$. Sci. China Phys. Mech. 57 (2), 330–335.CrossRefGoogle Scholar
Lin, Z., Wang, L. & Liao, S. 2017 On the origin of intrinsic randomness of Rayleigh–Bénard turbulence. Sci. China Phys. Mech. 60 (1), 1–13.CrossRefGoogle Scholar
Lorenz, E.N. 1963 Deterministic nonperiodic flow. J. Atmos. Sci. 20 (2), 130–141.2.0.CO;2>CrossRefGoogle Scholar
Lorenz, E.N. 1989 Computational chaos-a prelude to computational instability. Physica D 35 (3), 299–317.CrossRefGoogle Scholar
Lorenz, E.N. 1993 The Essence of Chaos. University of Washington Press.CrossRefGoogle Scholar
Lorenz, E.N. 2006 Computational periodicity as observed in a simple system. Tellus A 58 (5), 549–557.CrossRefGoogle Scholar
Lucarini, V. & Bódai, T. 2019 Transitions across melancholia states in a climate model: reconciling the deterministic and stochastic points of view. Phys. Rev. Lett. 122 (15), 158701.CrossRefGoogle Scholar
Lukes-Gerakopoulos, G., Voglis, N. & Efthymiopoulos, C. 2008 The production of Tsallis entropy in the limit of weak chaos and a new indicator of chaoticity. Physica A 387 (8), 1907–1925.CrossRefGoogle Scholar
Mezić, I. 2002 An extension of Prandtl–Batchelor theory and consequences for chaotic advection. Phys. Fluids 14 (9), L61–L64.CrossRefGoogle Scholar
Moffatt, H.K. & Proctor, M.R.E. 1985 Topological constraints associated with fast dynamo action. J. Fluid Mech. 154, 493–507.CrossRefGoogle Scholar
Moore, C.C. 2015 Ergodic theorem, ergodic theory, and statistical mechanics. Proc. Natl Acad. Sci. USA 112 (7), 1907–1911.CrossRefGoogle ScholarPubMed
von Neumann, J.V. 1932 Proof of the quasi-ergodic hypothesis. Proc. Natl Acad. Sci. USA 18 (1), 70–82.CrossRefGoogle Scholar
Newton, I. 1687 Philosophiae Naturalis Principia Mathematica. Royal Society.CrossRefGoogle Scholar
Oyanarte, P. 1990 MP – a multiple precision package. Comput. Phys. Commun. 59 (2), 345–358.Google Scholar
Parker, T.S. & Chua, L.O. 1989 Practical numerical algorithms for chaotic systems. Maths Comput. 66 (1), 125–128.Google Scholar
Peter, S. 1998 Explaining Chaos. Cambridge University Press.Google Scholar
Podvigina, O., Ashwin, P. & Hawker, D. 2006 Modelling instability of ABC flow using a mode interaction between steady and Hopf bifurcations with rotational symmetries of the cube. Physica D 215 (1), 62–79.CrossRefGoogle Scholar
Podvigina, O. & Pouquet, A. 1994 On the non-linear stability of the 1 : 1 : 1 ABC flow. Physica D 75 (4), 471–508.CrossRefGoogle Scholar
Poincaré, H. 1890 Sur le problème des trois corps et les équations de la dynamique. Acta Mathematica 13 (1), A3–A270.Google Scholar
Pope, S.B. 2001 Turbulent Flows. IOP.Google Scholar
Qin, S. & Liao, S. 2020 Influence of numerical noises on computer-generated simulation of spatio-temporal chaos. Chaos, Solitons Fractals 136, 109790.CrossRefGoogle Scholar
Qin, S. & Liao, S. 2022 Large-scale influence of numerical noises as artificial stochastic disturbances on a sustained turbulence. J. Fluid Mech. 948, A7.CrossRefGoogle Scholar
Ruelle, D. & Takens, F. 1971 On the nature of turbulence. Commun. Math. Phys. 20 (3), 167–192.CrossRefGoogle Scholar
Skokos, Ch. 2001 Alignment indices: a new, simple method for determining the ordered or chaotic nature of orbits. J. Phys. A: Math. Gen. 34 (47), 10029–10043.CrossRefGoogle Scholar
Śliwiak, A.A., Chandramoorthy, N. & Wang, Q. 2021 Computational assessment of smooth and rough parameter dependence of statistics in chaotic dynamical systems. Commun. Nonlinear Sci. Numer. Simul. 101, 105906.CrossRefGoogle Scholar
Sprott, J.C. 2010 Elegant Chaos: Algebraically Simple Chaotic Flows. World Scientific.CrossRefGoogle Scholar
Stankevich, N., Kazakov, A. & Gonchenko, S. 2020 Scenarios of hyperchaos occurrence in 4D Rössler system. Chaos 30, 123129.CrossRefGoogle ScholarPubMed
Teixeira, J., Reynolds, C.A. & Judd, K. 2007 Time step sensitivity of nonlinear atmospheric models: numerical convergence, truncation error growth, and ensemble design. J. Atmos. Sci. 64 (1), 175–189.CrossRefGoogle Scholar
Van Gorder, R.A. 2013 Shilnikov chaos in the 4D Lorenz–Stenflo system modeling the time evolution of nonlinear acoustic-gravity waves in a rotating atmosphere. Nonlinear Dyn. 72 (4), 837–851.CrossRefGoogle Scholar
Whyte, C. 2018 Watch the weird new solutions to the baffling three-body problem. New Sci. Available at: https://www.newscientist.com/article/2170161-watch-the-weird-new-solutions-to-the-baffling-three-body-problem/.Google Scholar
Xu, T., Li, J., Li, Z. & Liao, S. 2021 Accurate predictions of chaotic motion of a free fall disk. Phys. Fluids 33 (3), 037111.CrossRefGoogle Scholar
Yang, Y., Qin, S. & Liao, S. 2023 Ultra-chaos of a mobile robot: a higher disorder than normal-chaos. Chaos, Solitons Fractals 167, 113037.CrossRefGoogle Scholar

Qin and Liao supplementary material

Comparison of the normal-chaotic (left) and ultra-chaotic trajectory (right) of the ABC flow in the case of A =1, B =0.7 and C =0.43. Left: starting from (0,-0.1,0); Right: starting from (-0.1,0.1,0).

Download Qin and Liao supplementary material(Video)
Video 6.6 MB