Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-19T19:02:23.320Z Has data issue: false hasContentIssue false
  • English
  • Français

Interfacial instabilities driven by co-directional rarefaction and shock waves

Published online by Cambridge University Press:  31 January 2024

Xing Gao ,
Xu Guo Open the ORCID record for Xu Guo [Opens in a new window] ,
Zhigang Zhai Open the ORCID record for Zhigang Zhai [Opens in a new window]  and
Xisheng Luo Open the ORCID record for Xisheng Luo [Opens in a new window]
Xing Gao
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China
Xu Guo*
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China
Zhigang Zhai*
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China
Xisheng Luo
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, PR China State Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China
*
†Email addresses for correspondence: clguoxu@ustc.edu.cn, sanjing@ustc.edu.cn
†Email addresses for correspondence: clguoxu@ustc.edu.cn, sanjing@ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

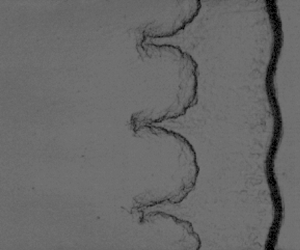
We report the first experiments on hydrodynamic instabilities of a single-mode light/heavy interface driven by co-directional rarefaction and shock waves. The experiments are conducted in a specially designed rarefaction-shock tube that enables the decoupling of interfacial instabilities caused by these co-directional waves. After the impacts of rarefaction and shock waves, the interface evolution transitions into Richtmyer–Meshkov unstable states from Rayleigh–Taylor (RT) stable states, which is different from the finding in the previous case with counter-directional rarefaction and shock waves. A scaling method is proposed, which effectively collapses the RT stable perturbation growths. An analytical theory for predicting the time-dependent acceleration and density induced by rarefaction waves is established. Based on the analytical theory, the model proposed by Mikaelian (Phys. Fluids, vol. 21, 2009, p. 024103) is revised to provide a good description of the dimensionless RT stable behaviour. Before the shock arrival, the unequal interface velocities, caused by rarefaction-induced uneven vorticity, result in a V-shape-like interface. The linear growth rate of the amplitude is insensitive to the pre-shock interface shape, and can be well predicted by the linear superposition of growth rates induced by rarefaction and shock waves. The nonlinear growth rate is higher than that of a pure single-mode case, which can be predicted by the nonlinear models (Sadot et al., Phys. Rev. Lett., vol. 80, 1998, pp. 1654–1657; Dimonte & Ramaprabhu, Phys. Fluids, vol. 22, 2010, p. 014104).

JFM classification

Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 980 , 10 February 2024 , A20
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alon, U., Hecht, J., Mukamel, D. & Shvarts, D. 1994 Scale invariant mixing rates of hydrodynamically unstable interface. Phys. Rev. Lett. 72, 2867–2870.CrossRefGoogle Scholar
Balakumar, B.J., Orlicz, G.C., Ristorcelli, J.R., Balasubramanian, S., Prestridge, K.P. & Tomkins, C.D. 2012 Turbulent mixing in a Richtmyer–Meshkov fluid layer after reshock: velocity and density statistics. J. Fluid Mech. 696, 67–93.CrossRefGoogle Scholar
Balakumar, B.J., Orlicz, G.C., Tomkins, C.D. & Prestridge, K.P. 2008 Simultaneous particle-image velocimetry-planar laser-induced fluorescence measurements of Richtmyer–Meshkov instability growth in a gas curtain with and without reshock. Phys. Fluids 20, 124103.CrossRefGoogle Scholar
Betti, R. & Hurricane, O.A. 2016 Inertial-confinement fusion with lasers. Nat. Phys. 12, 435–448.CrossRefGoogle Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.CrossRefGoogle Scholar
Charakhch'yan, A.A. 2001 Reshocking at the non-linear stage of Richtmyer–Meshkov instability. Plasma Phys. Control. Fusion 43, 1169.CrossRefGoogle Scholar
Chen, C., Wang, H., Zhai, Z. & Luo, X. 2023 a Attenuation of perturbation growth of single-mode SF$_6$–air interface through reflected rarefaction waves. J. Fluid Mech. 969, R1.CrossRefGoogle Scholar
Chen, C., Xing, Y., Wang, H., Zhai, Z. & Luo, X. 2023 b Freeze-out of perturbation growth of single-mode helium-air interface through reflected shock in Richtmyer–Meshkov flows. J. Fluid Mech. 956, R2.CrossRefGoogle Scholar
Chu, Y., Wang, Z., Qi, J., Xu, Z. & Li, Z. 2022 Numerical performance assessment of double-shell targets for Z-pinch dynamic hohlraum. Matt. Radiat. Extrem. 7, 035902.CrossRefGoogle Scholar
Clark, D.S., et al. 2016 Three-dimensional simulations of low foot and high foot implosion experiments on the national ignition facility. Phys. Plasmas 23, 056302.CrossRefGoogle Scholar
Collins, B.D. & Jacobs, J.W. 2002 PLIF flow visualization and measurements of the Richtmyer–Meshkov instability of an air/SF$_6$ interface. J. Fluid Mech. 464, 113–136.CrossRefGoogle Scholar
Cong, Z., Guo, X., Si, T. & Luo, X. 2022 Experimental and theoretical studies on heavy fluid layers with reshock. Phys. Fluids 34, 104108.CrossRefGoogle Scholar
Dell, Z.R., Stellingwerf, R.F. & Abarzhi, S.I. 2015 Effect of initial perturbation amplitude on Richtmyer–Meshkov flows induced by strong shocks. Phys. Plasmas 22, 092711.CrossRefGoogle Scholar
Dimonte, G. & Ramaprabhu, P. 2010 Simulations and model of the nonlinear Richtmyer–Meshkov instability. Phys. Fluids 22, 014104.CrossRefGoogle Scholar
Ding, J., Si, T., Chen, M., Zhai, Z., Lu, X. & Luo, X. 2017 On the interaction of a planar shock with a three-dimensional light gas cylinder. J. Fluid Mech. 828, 289–317.CrossRefGoogle Scholar
Farley, D.R., Peyser, T.A., Logory, L.M., Murray, S.D. & Burke, E.W. 1999 High Mach number mix instability experiments of an unstable density interface using a single-mode, nonlinear initial perturbation. Phys. Plasmas 6, 4304–4317.CrossRefGoogle Scholar
Goncharov, V.N. 2002 Analytical model of nonlinear, single-mode, classical Rayleigh–Taylor instability at arbitrary Atwood numbers. Phys. Rev. Lett. 88, 134502.CrossRefGoogle ScholarPubMed
Guo, X., Cong, Z., Si, T. & Luo, X. 2022 a Shock-tube studies of single- and quasi-single-mode perturbation growth in Richtmyer–Meshkov flows with reshock. J. Fluid Mech. 941, A65.CrossRefGoogle Scholar
Guo, X., Si, T., Zhai, Z. & Luo, X. 2022 b Large-amplitude effects on interface perturbation growth in Richtmyer–Meshkov flows with reshock. Phys. Fluids 34, 082118.CrossRefGoogle Scholar
Guo, X., Zhai, Z., Ding, J., Si, T. & Luo, X. 2020 Effects of transverse shock waves on early evolution of multi-mode chevron interface. Phys. Fluids 32, 106101.CrossRefGoogle Scholar
Han, Z. & Yin, X. 1993 Shock Dynamics. Kluwer Academic Publishers and Science Press.CrossRefGoogle Scholar
Hecht, J., Alon, U. & Shvarts, D. 1994 Potential flow models of Rayleigh–Taylor and Richtmyer–Meshkov bubble fronts. Phys. Fluids 6, 4019–4030.CrossRefGoogle Scholar
Hill, D.J., Pantano, C. & Pullin, D.I. 2006 Large-eddy simulation and multiscale modelling of a Richtmyer–Meshkov instability with reshock. J. Fluid Mech. 557, 29–61.CrossRefGoogle Scholar
Holmes, R.L., Dimonte, G., Fryxell, B., Gittings, M.L., Grove, J.W., Schneider, M., Sharp, D.H., Velikovich, A.L., Weaver, R.P. & Zhang, Q. 1999 Richtmyer–Meshkov instability growth: experiment, simulation and theory. J. Fluid Mech. 389, 55–79.CrossRefGoogle Scholar
Jacobs, J.W. & Krivets, V.V. 2005 Experiments on the late-time development of single-mode Richtmyer–Meshkov instability. Phys. Fluids 17, 034105.CrossRefGoogle Scholar
Jones, M.A. & Jacobs, J.W. 1997 A membraneless experiment for the study of Richtmyer–Meshkov instability of a shock-accelerated gas interface. Phys. Fluids 9, 3078–3085.CrossRefGoogle Scholar
Kuranz, C.C, Park, H. -S., Huntington, C.M., Miles, A.R., Remington, B.A., Plewa, T., Trantham, M.R., Robey, H.F., Shvarts, D. & Shimony, A. 2018 How high energy fluxes may affect Rayleigh–Taylor instability growth in young supernova remnants. Nat. commun. 9, 1–6.CrossRefGoogle ScholarPubMed
Latini, M., Schilling, O. & Don, W.S. 2007 High-resolution simulations and modeling of reshocked single-mode Richtmyer–Meshkov instability: comparison to experimental data and to amplitude growth model predictions. Phys. Fluids 19, 024104.CrossRefGoogle Scholar
Layzer, D. 1955 On the instability of superposed fluids in a gravitational field. Astrophys. J. 122, 1–12.CrossRefGoogle Scholar
Li, C. & Book, D.L 1991 Instability generated by acceleration due to rarefaction waves. Phys. Rev. A 43, 3153.CrossRefGoogle ScholarPubMed
Li, C., Kailasanath, K. & Book, D.L. 1991 Mixing enhancement by expansion waves in supersonic flows of different densities. Phys. Fluids A 3, 1369–1373.CrossRefGoogle Scholar
Li, H., He, Z., Zhang, Y. & Tian, B. 2019 On the role of rarefaction/compression waves in Richtmyer–Meshkov instability with reshock. Phys. Fluids 31, 054102.CrossRefGoogle Scholar
Li, H., Tian, B., He, Z. & Zhang, Y. 2021 Growth mechanism of interfacial fluid-mixing width induced by successive nonlinear wave interactions. Phys. Rev. E 103, 053109.CrossRefGoogle ScholarPubMed
Li, J., Cao, Q., Wang, H., Zhai, Z. & Luo, X. 2023 New interface formation method for shock-interface interaction studies. Exp. Fluids 64, 170.CrossRefGoogle Scholar
Li, J., Ding, J., Luo, X. & Zou, L. 2022 Instability of a heavy gas layer induced by a cylindrical convergent shock. Phys. Fluids 34, 042123.CrossRefGoogle Scholar
Liang, Y. & Luo, X. 2021 On shock-induced heavy-fluid-layer evolution. J. Fluid Mech. 920, A13.CrossRefGoogle Scholar
Liang, Y., Zhai, Z., Ding, J. & Luo, X. 2019 Richtmyer–Meshkov instability on a quasi-single-mode interface. J. Fluid Mech. 872, 729–751.CrossRefGoogle Scholar
Liang, Y., Zhai, Z., Luo, X. & Wen, C. 2020 Interfacial instability at a heavy/light interface induced by rarefaction waves. J. Fluid Mech. 885, A42.CrossRefGoogle Scholar
Lindl, J., Landen, O., Edwards, J., Moses, E. & Team, N. 2014 Review of the national ignition campaign 2009–2012. Phys. Plasmas 21, 020501.CrossRefGoogle Scholar
Liu, C., Zhang, Y. & Xiao, Z. 2023 A unified theoretical model for spatiotemporal development of Rayleigh–Taylor and Richtmyer–Meshkov fingers. J. Fluid Mech. 954, A13.CrossRefGoogle Scholar
Liu, L., Liang, Y., Ding, J., Liu, N. & Luo, X. 2018 An elaborate experiment on the single-mode Richtmyer–Meshkov instability. J. Fluid Mech. 853, R2.CrossRefGoogle Scholar
Lombardini, M., Hill, D.J., Pullin, D.I. & Meiron, D.I. 2011 Atwood ratio dependence of Richtmyer–Meshkov flows under reshock conditions using large-eddy simulations. J. Fluid Mech. 670, 439–480.CrossRefGoogle Scholar
Luo, X., Liang, Y., Si, T. & Zhai, Z. 2019 Effects of non-periodic portions of interface on Richtmyer–Meshkov instability. J. Fluid Mech. 861, 309–327.CrossRefGoogle Scholar
Mansoor, M.M., Dalton, S.M., Martinez, A.A., Desjardins, T., Charonko, J.J. & Prestridge, K.P. 2020 The effect of initial conditions on mixing transition of the Richtmyer–Meshkov instability. J. Fluid Mech. 904, A3.CrossRefGoogle Scholar
McFarland, J.A., Greenough, J.A. & Ranjan, D. 2014 Simulations and analysis of the reshocked inclined interface Richtmyer–Meshkov instability for linear and nonlinear interface perturbations. J. Fluids Engng 136, 071203.CrossRefGoogle Scholar
McFarland, J.A., Reilly, D., Black, W., Greenough, J.A. & Ranjan, D. 2015 Modal interactions between a large-wavelength inclined interface and small-wavelength multimode perturbations in a Richtmyer–Meshkov instability. Phys. Rev. E 92, 013023.CrossRefGoogle Scholar
Meshkov, E.E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4, 101–104.CrossRefGoogle Scholar
Mikaelian, K.O. 1985 Richtmyer–Meshkov instabilities in stratified fluids. Phys. Rev. A 31, 410–419.CrossRefGoogle ScholarPubMed
Mikaelian, K.O. 2005 Richtmyer–Meshkov instability of arbitrary shapes. Phys. Fluids 17, 034101.CrossRefGoogle Scholar
Mikaelian, K.O. 2009 Reshocks, rarefactions, and the generalized Layzer model for hydrodynamic instabilities. Phys. Fluids 21, 024103.CrossRefGoogle Scholar
Mohaghar, M. 2019 Effects of initial conditions and Mach number on turbulent mixing transition of shock-driven variable-density flow. PhD thesis, Georgia Institute of Technology.Google Scholar
Mohaghar, M., Carter, J., Musci, B., Reilly, D., McFarland, J. & Ranjan, D. 2017 Evaluation of turbulent mixing transition in a shock-driven variable-density flow. J. Fluid Mech. 831, 779–825.CrossRefGoogle Scholar
Mohaghar, M., Carter, J., Pathikonda, G. & Ranjan, D. 2019 The transition to turbulence in shock-driven mixing: effects of Mach number and initial conditions. J. Fluid Mech. 871, 595–635.CrossRefGoogle Scholar
Montgomery, D.S., et al. 2018 Design considerations for indirectly driven double shell capsules. Phys. Plasmas 25, 092706.CrossRefGoogle Scholar
Morgan, R.V., Cabot, W.H., Greenough, J.A. & Jacobs, J.W. 2018 Rarefaction-driven Rayleigh–Taylor instability. Part 2. Experiments and simulations in the nonlinear regime. J. Fluid Mech. 838, 320–355.CrossRefGoogle Scholar
Morgan, R.V. & Jacobs, J.W. 2020 Experiments and simulations on the turbulent, rarefaction wave driven Rayleigh–Taylor instability. J. Fluids Engng 142, 121101.CrossRefGoogle Scholar
Morgan, R.V., Likhachev, O.A. & Jacobs, J.W. 2016 Rarefaction-driven Rayleigh–Taylor instability. Part 1. Diffuse-interface linear stability measurements and theory. J. Fluid Mech. 791, 34–60.CrossRefGoogle Scholar
Motl, B., Oakley, J., Ranjan, D., Weber, C., Anderson, M. & Bonazza, R. 2009 Experimental validation of a Richtmyer–Meshkov scaling law over large density ratio and shock strength ranges. Phys. Fluids 21, 126102.CrossRefGoogle Scholar
Musci, B., Petter, S., Pathikonda, G., Ochs, B. & Ranjan, D. 2020 Supernova hydrodynamics: a lab-scale study of the blast-driven instability using high-speed diagnostics. Astrophys. J. 896, 92.CrossRefGoogle Scholar
Peterson, J.R., Johnson, B.M. & Haan, S.W. 2018 Instability growth seeded by DT density perturbations in ICF capsules. Phys. Plasmas 25, 092705.CrossRefGoogle Scholar
Ramaprabhu, P., Dimonte, G., Young, Y., Calder, A.C. & Fryxell, B. 2006 Limits of the potential flow approach to the single-mode Rayleigh–Taylor problem. Phys. Rev. E 74, 066308.CrossRefGoogle Scholar
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock-bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.CrossRefGoogle Scholar
Rayleigh, Lord 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177.Google Scholar
Reese, D.T., Ames, A.M., Noble, C.D., Oakley, J.G., Rothamer, D.A. & Bonazza, R. 2018 Simultaneous direct measurements of concentration and velocity in the Richtmyer–Meshkov instability. J. Fluid Mech. 849, 541–575.CrossRefGoogle Scholar
Richtmyer, R.D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.CrossRefGoogle Scholar
Sadot, O., Erez, L., Alon, U., Oron, D., Levin, L.A., Erez, G., Ben-Dor, G. & Shvarts, D. 1998 Study of nonlinear evolution of single-mode and two-bubble interaction under Richtmyer–Meshkov instability. Phys. Rev. Lett. 80, 1654–1657.CrossRefGoogle Scholar
Sadot, O., Rikanati, A., Oron, D., Ben-Dor, G. & Shvarts, D. 2003 An experimental study of the high Mach number and high initial-amplitude effects on the evolution of the single-mode Richtmyer–Meshkov instability. Laser Part. Beams 21, 341–346.CrossRefGoogle Scholar
Schilling, O., Latini, M. & Don, W.S. 2007 Physics of reshock and mixing in single-mode Richtmyer–Meshkov instability. Phys. Rev. E 76, 026319.CrossRefGoogle ScholarPubMed
Sewell, E.G., Ferguson, K.J., Krivets, V.V. & Jacobs, J.W. 2021 Time-resolved particle image velocimetry measurements of the turbulent Richtmyer–Meshkov instability. J. Fluid Mech. 917, A41.CrossRefGoogle Scholar
Taylor, G.I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 201, 192–196.Google Scholar
Thornber, B., Griffond, J., Bigdelou, P., Boureima, I., Ramaprabhu, P., Schilling, O. & Williams, R.J.R. 2019 Turbulent transport and mixing in the multimode narrowband Richtmyer–Meshkov instability. Phys. Fluids 31, 096105.CrossRefGoogle Scholar
Vandenboomgaerde, M., Mügler, C. & Gauthier, S. 1998 Impulsive model for the Richtmyer–Meshkov instability. Phys. Rev. E 58, 1874–1882.CrossRefGoogle Scholar
Vanderboomgaerde, M., Souffland, D., Mariani, C., Biamino, L., Jourdan, G. & Houas, L. 2014 Investigation of the Richtmyer–Meshkov instability with stereolithographed interfaces. Phys. Fluids 26, 024109.Google Scholar
Wang, H., Wang, H., Zhai, Z. & Luo, X. 2022 a Effects of obstacles on shock-induced perturbation growth. Phys. Fluids 34, 086112.CrossRefGoogle Scholar
Wang, R., Song, Y., Ma, Z., Ma, D., Wang, L. & Wang, P. 2022 b The transition to turbulence in rarefaction-driven Rayleigh–Taylor mixing: effects of diffuse interface. Phys. Fluids 34, 015125.CrossRefGoogle Scholar
Wang, R., Song, Y., Ma, Z., Zhang, C., Shi, X., Wang, L. & Wang, P. 2022 c Transitional model for rarefaction-driven Rayleigh–Taylor mixing on the diffuse interface. Phys. Fluids 34, 075136.CrossRefGoogle Scholar
Wei, T. & Livescu, D. 2012 Late-time quadratic growth in single-mode Rayleigh–Taylor instability. Phys. Rev. E 86, 046405.CrossRefGoogle ScholarPubMed
Wilkinson, J.P. & Jacobs, J.W. 2007 Experimental study of the single-mode three-dimensional Rayleigh–Taylor instability. Phys. Fluids 19, 124102.CrossRefGoogle Scholar
Yang, Q., Chang, J. & Bao, W. 2014 Richtmyer–Meshkov instability induced mixing enhancement in the scramjet combustor with a central strut. Adv. Mech. Engng 6, 614189.CrossRefGoogle Scholar
Zhang, Q. 1998 Analytical solutions of Layzer-type approach to unstable interfacial fluid mixing. Phys. Rev. Lett. 81, 3391.CrossRefGoogle Scholar
Zhang, Q. & Guo, W. 2016 Universality of finger growth in two-dimensional Rayleigh–Taylor and Richtmyer–Meshkov instabilities with all density ratios. J. Fluid Mech. 786, 47–61.CrossRefGoogle Scholar
Zhang, Q. & Sohn, S.I. 1996 An analytical nonlinear theory of Richtmyer–Meshkov instability. Phys. Lett. A 212, 149–155.CrossRefGoogle Scholar
Zhang, Q. & Sohn, S.I. 1997 Nonlinear theory of unstable fluid mixing driven by shock wave. Phys. Fluids 9, 1106–1124.CrossRefGoogle Scholar
Zhou, Y. 2017 a Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 720–722, 1–136.Google Scholar
Zhou, Y. 2017 b Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II. Phys. Rep. 723–725, 1–160.Google Scholar
Zhou, Y., Clark, T.T., Clark, D.S., Glendinning, S.G., Skinner, M.A., Huntington, C.M., Hurricane, O.A., Dimits, A.M. & Remington, B.A. 2019 Turbulent mixing and transition criteria of flows induced by hydrodynamic instabilities. Phys. Plasmas 26, 080901.CrossRefGoogle Scholar
Zhou, Y., et al. 2021 Rayleigh–Taylor and Richtmyer–Meshkov instabilities: a journey through scales. Physica D 423, 132838.CrossRefGoogle Scholar
Zucker, R.D. & Biblarz, O. 2019 Fundamentals of Gas Dynamics. John Wiley & Sons.Google Scholar