Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-01T00:02:07.265Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial wave super-attractor in a truncated elliptic cone

Published online by Cambridge University Press:  26 January 2024

Benjamin Favier Open the ORCID record for Benjamin Favier [Opens in a new window]  and
Stéphane Le Dizès Open the ORCID record for Stéphane Le Dizès [Opens in a new window]
Benjamin Favier*
Affiliation:
Aix Marseille Univ, CNRS, Centrale Marseille, IRPHE, Marseille, France
Stéphane Le Dizès
Affiliation:
Aix Marseille Univ, CNRS, Centrale Marseille, IRPHE, Marseille, France
*
†Email address for correspondence: benjamin.favier@univ-amu.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

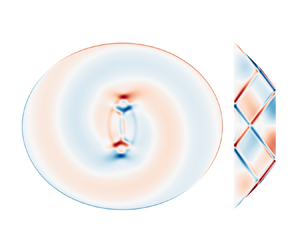
We consider inertial waves propagating in a fluid contained in a non-axisymmetric three-dimensional rotating cavity. We focus on the particular case of a fluid enclosed inside a truncated cone or frustum, which is the volume that lies between two horizontal parallel planes cutting an upright cone. While this geometry has been studied in the past, we generalise it by breaking its axisymmetry and consider the case of a truncated elliptic cone for which the horizontal sections are elliptic instead of circular. The problem is first tackled using ray tracing, where local wave packets are geometrically propagated and reflected within the closed volume without attenuation. We complement these results with a local asymptotic analysis and numerical simulations of the original linear viscous problem. We show that the attractors, well known in two dimensional or axisymmetric domains, can be trapped in a particular plane in three dimensions provided that the axisymmetry of the domain is broken. Contrary to previous examples of attractors in three-dimensional domains, all rays converge towards the same limit cycle regardless of initial conditions, and it is localised in the bulk of the fluid.

JFM classification

Geophysical and Geological Flows: Waves in rotating fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 980 , 10 February 2024 , A6
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bajars, J., Frank, J. & Maas, L.R.M. 2013 On the appearance of internal wave attractors due to an initial or parametrically excited disturbance. J. Fluid Mech. 714, 283–311.Google Scholar
Beardsley, R.C. 1970 An experimental study of inertial waves in a closed cone. Stud. Appl. Maths 49 (2), 187–196.Google Scholar
Beckebanze, F., Brouzet, C., Sibgatullin, I.N. & Maas, L.R.M. 2018 Damping of quasi-two-dimensional internal wave attractors by rigid-wall friction. J. Fluid Mech. 841, 615–635.Google Scholar
Beckebanze, F., Grayson, K.M., Maas, L.R.M. & Dalziel, S.B. 2021 Experimental evidence of internal wave attractor signatures hidden in large-amplitude multi-frequency wave fields. J. Fluid Mech. 915, A41.Google Scholar
Beckebanze, F. & Keady, G. 2016 On functional equations leading to exact solutions for standing internal waves. Wave Motion 60, 181–195.Google Scholar
Borcia, I.D. & Harlander, U. 2013 Inertial waves in a rotating annulus with inclined inner cylinder: comparing the spectrum of wave attractor frequency bands and the eigenspectrum in the limit of zero inclination. Theor. Comput. Fluid Dyn. 27, 397–413.CrossRefGoogle Scholar
Boury, S., Sibgatullin, I., Ermanyuk, E., Shmakova, N., Odier, P., Joubaud, S., Maas, L.R.M. & Dauxois, T. 2021 Vortex cluster arising from an axisymmetric inertial wave attractor. J. Fluid Mech. 926, A12.Google Scholar
Bretherton, F.P. 1964 Low frequency oscillations trapped near the equator. Tellus 16, 181–185.CrossRefGoogle Scholar
Brouzet, C., Ermanyuk, E., Joubaud, S., Pillet, G. & Dauxois, T. 2017 Internal wave attractors: different scenarios of instability. J. Fluid Mech. 811, 544–568.CrossRefGoogle Scholar
Brouzet, C., Ermanyuk, E.V., Joubaud, S., Sibgatullin, I. & Dauxois, T. 2016 a Energy cascade in internal-wave attractors. Europhys. Lett. 113 (4), 44001.Google Scholar
Brouzet, C., Sibgatullin, I.N., Scolan, H., Ermanyuk, E.V. & Dauxois, T. 2016 b Internal waves attractors examined using laboratory experiments and 3D simulations. J. Fluid Mech. 793, 109–131.Google Scholar
Brunet, M., Dauxois, T. & Cortet, P.-P. 2019 Linear and nonlinear regimes of an inertial wave attractor. Phys. Rev. Fluids 4 (3), 034801.Google Scholar
Bühler, O. & Muller, C.J. 2007 Instability and focusing of internal tides in the deep ocean. J. Fluid Mech. 588, 1–28.Google Scholar
Dauxois, T., Joubaud, S., Odier, P. & Venaille, A. 2018 Instabilities of internal gravity wave beams. Annu. Rev. Fluid Mech. 50, 1–28.Google Scholar
Deville, M.O., Fischer, P.F. & Mund, E.H. 2002 High-Order Methods for Incompressible Fluid Flow. Cambridge University Press.Google Scholar
Drijfhout, S. & Maas, L.R.M. 2007 Impact of channel geometry and rotation on the trapping of internal tides. J. Phys. Oceanogr. 37, 2740–63.CrossRefGoogle Scholar
Dyatlov, S., Wang, J. & Zworski, M. 2022 Mathematics of internal waves in a 2D aquarium. J. Anal. PDE (submitted) arXiv:2112.10191.Google Scholar
Echeverri, P., Yokossi, T., Balmforth, N.J. & Peacock, T. 2011 Tidally generated internal-wave attractors between double ridges. J. Fluid Mech. 669, 354–374.CrossRefGoogle Scholar
Favier, B., Barker, A.J., Baruteau, C. & Ogilvie, G.I. 2014 Non-linear evolution of tidally forced inertial waves in rotating fluid bodies. Mon. Not. R. Astron. Soc. 439, 845–860.Google Scholar
Fischer, P.F. 1997 An overlapping Schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133, 84–101.CrossRefGoogle Scholar
Grisouard, N., Staquet, C. & Pairaud, I. 2008 Numerical simulation of a two-dimensional internal wave atractor. J. Fluid Mech. 614, 1–14.CrossRefGoogle Scholar
Hazewinkel, J., Tsimitri, C., Maas, L.R.M. & Dalziel, S.B. 2010 Observations on the robustness of internal wave attractors to perturbations. Phys. Fluids 22, 107102.CrossRefGoogle Scholar
Hazewinkel, J., Van Breevoort, P., Dalziel, S.B. & Maas, L.R.M. 2008 Observations of the wavenumber spectrum and evolution of an internal wave attractor. J. Fluid Mech. 598, 373–382.CrossRefGoogle Scholar
He, J., Favier, B., Rieutord, M. & Le Dizès, S. 2022 Internal shear layers in librating spherical shells: the case of periodic characteristic paths. J. Fluid Mech. 939, A3.Google Scholar
He, J., Favier, B., Rieutord, M. & Le Dizès, S. 2023 Internal shear layers in librating spherical shells: the case of attractors. J. Fluid Mech. 974, A3.Google Scholar
Henderson, G.A. & Aldridge, K.D. 1992 A finite-element method for inertial waves in a frustum. J. Fluid Mech. 234, 317–327.Google Scholar
Jouve, L. & Ogilvie, G.I. 2014 Direct numerical simulations of an inertial wave attractor in linear and nonlinear regimes. J. Fluid Mech. 745, 223–250.CrossRefGoogle Scholar
Klein, M., Seelig, T., Kurgansky, M., Ghasemi, A.V., Borcia, I.D., Will, A., Schaller, E., Egbers, C. & Harlander, U. 2014 Inertial wave excitation and focusing in a liquid bounded by a frustrum and a cylinder. J. Fluid Mech. 751, 255–297.Google Scholar
Kudrolli, A., Abraham, M.C. & Gollub, J.P. 2001 Scarred patterns in surface waves. Phys. Rev. E 63 (2), 026208.Google Scholar
Maas, L.R.M. 2001 Wave focusing and ensuing mean flow due to symmetry breaking in rotating fluids. J. Fluid Mech. 437, 13–28.Google Scholar
Maas, L.R.M. 2005 Wave attractors: linear yet nonlinear. Intl J. Bifurcation Chaos 15 (09), 2757–2782.Google Scholar
Maas, L.R.M. 2009 Exact analytic self-similar solution of a wave attractor field. Physica D 238, 502–505.Google Scholar
Maas, L.R.M., Benielli, D., Sommeria, J. & Lam, F.-P.A. 1997 Observation of an internal wave attractor in a confined, stably stratified fluid. Nature 388, 557–561.Google Scholar
Maas, L.R.M. & Lam, F.-P. 1995 Geometric focusing of internal waves. J. Fluid Mech. 300, 1–41.Google Scholar
Makridin, Z.V., Khe, A.K., Sibgatullin, I.N. & Ermanyuk, E.V. 2023 Forced internal wave attractors: linear inviscid theory. Phys. Rev. Fluids 8, 084801.Google Scholar
Manders, A.M., Duistermaat, J.J. & Maas, L.R.M. 2003 Wave attractors in a smooth convex enclosed geometry. Physica D: Nonlinear Phenom. 186 (3–4), 109–132.Google Scholar
Manders, A.M. & Maas, L.R.M. 2003 Observations of intertial waves in a rectangular basin with one sloping boundary. J. Fluid Mech. 493, 59–88.Google Scholar
Manders, A.M. & Maas, L.R.M. 2004 On the three-dimensional structure of the inertial wave filed in a rectangular basin with one sloping boundary. Fluid Dyn. Res. 35, 1–21.Google Scholar
Manders, A.M., Maas, L.R.M. & Gerkema, T. 2004 Observation of internal tides in the Mozambique Channel. J. Geophys. Res. 109, C12034.Google Scholar
Ogilvie, G.I. & Lin, D.N.C. 2004 Tidal dissipation in rotating giant planets. Astroph. J. 610, 477–509.Google Scholar
Pacary, C. 2023 Dynamique des milieux stratifiés ou tournants: Attracteurs d'ondes axisymétriques, interaction non-linéaire et panaches en rotation. PhD thesis, Ecole Normale Supérieur de Lyon.Google Scholar
Pacary, C., Dauxois, T., Ermanyuk, E., Metz, P., Moulin, M. & Joubaud, S. 2023 Observation of inertia-gravity wave attractors in an axisymmetric enclosed basin. Phys. Rev. Fluids 8, 104892.Google Scholar
Phillips, O.M. 1966 The Dynamics of the Upper Ocean. Cambridge University Press.Google Scholar
Pillet, G., Ermanyuk, E.V., Maas, L.R.M., Sibgatullin, I.N. & Dauxois, T. 2018 Internal wave attractors in three-dimensional geometries: trapping by oblique reflection. J. Fluid Mech. 845, 203–225.Google Scholar
Pillet, G., Maas, L.R.M. & Dauxois, T. 2019 Internal wave attractors in 3d geometries: a dynamical systems approach. Eur. J. Mech. (B/Fluids) 77, 1–16.Google Scholar
Rabitti, A. & Maas, L.R.M. 2013 Meridional trraping and zonal propagation of inertial waves in a rotating shell. J. Fluid Mech. 729, 445–470.Google Scholar
Rabitti, A. & Maas, L.R.M. 2014 Inertial wave rays in rotating spherical fluid domains. J. Fluid Mech. 758, 621–654.CrossRefGoogle Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2000 Wave attractors in rotating fluids: a paradigm for ill-posed cauchy problems. Phys. Rev. Lett. 85, 4277–4280.Google Scholar
Rieutord, M. & Valdettaro, L. 1997 Inertial waves in a rotating spherical shell. J. Fluid Mech. 341, 77–99.Google Scholar
Rieutord, M. & Valdettaro, L. 2010 Viscous dissipation by tidally forced inertial modes in a rotating spherical shell. J. Fluid Mech. 643, 363–394.Google Scholar
Rieutord, M. & Valdettaro, L. 2018 Axisymmetric inertial modes in a spherical shell at low Ekman numbers. J. Fluid Mech. 844, 597–634.Google Scholar
Rieutord, M., Valdettaro, L. & Georgeot, B. 2002 Analysis of singular inertial modes in a spherical shell: the slender toroidal shell model. J. Fluid Mech. 463, 345–360.Google Scholar
Ryazanov, D.A., Providukhina, M.I., Sibgatullin, I.N. & Ermanyuk, E.V. 2021 Biharmonic attractors of internal gravity waves. Fluid Dyn. 56, 403–412.Google Scholar
Scolan, H., Ermanyuk, E. & Dauxois, T. 2013 Nonlinear fate of internal waves attractors. Phys. Rev. Lett. 110, 234501.Google Scholar
Sibgatullin, I., Ermanyuk, E., Maas, L.R.M., Xu, X. & Dauxois, T. 2017 Direct numerical simulation of three-dimensional inertial wave attractors. In 2017 Ivannikov ISPRAS Open Conference (ISPRAS), pp. 137–143. IEEE.Google Scholar
Sibgatullin, I., Xu, X., Tretyakov, A. & Ermanyuk, E. 2019 Influence of geometry on energy flow and instability in inertial wave attractors for rotating annular frustum. In AIP Conference Proceedings (ed. T. Simos & C. Tsitouras), vol. 2116. AIP Publishing.Google Scholar
Staquet, C. & Sommeria, J. 2002 Internal gravity waves: from instabilities to turbulence. Annu. Rev. Fluid Mech. 34 (1), 559–593.Google Scholar
Stern, M.E. 1963 Trapping of low frequency oscillations in an equatorial “boundary layer”. Tellus 15, 246–250.Google Scholar
Stewartson, K. 1972 On trapped oscillations in a slightly viscous rotating fluid. J. Fluid Mech. 54, 749–761.Google Scholar
Tang, W. & Peacock, T. 2010 Lagrangian coherent structures and internal wave attractors. Chaos 20, 017508.CrossRefGoogle ScholarPubMed
de Verdière, Y.C. & Saint-Raymond, L. 2020 Attractors for two-dimensional waves with homogeneous Hamiltonians of degree 0. Commun. Pure Appl. Maths 73, 421–462.CrossRefGoogle Scholar
Wang, G., Zheng, Q., Lin, M., Dai, D. & Qiao, F. 2015 Three dimensional simulation of internal wave attractors in the Luzon Strait. Acta Oceanol. Sin. 34, 14–21.Google Scholar
Wu, K., Welfert, B.D. & Lopez, J.M. 2023 Inertial wave attractors in librating cuboids. J. Fluid Mech. 973, A20.Google Scholar
Wunsch, C. 1975 Internal tides in the ocean. Rev. Geophys. Space Phys. 13, 167–182.Google Scholar
Zahn, J.-P. 1975 Tidal friction in close binary systems. Astron. Astrophys. 57, 383–394.Google Scholar
Supplementary material: File

Favier and Le Dizès supplementary movie 1

Trajectories of many particles randomly initialised within the volume. Each particle is travelling along the ray path at constant speed. Each particle is plotted as an empty symbol along with a line indicating past positions. The left panel shows top and side views while the right panel shows a 3D top view. The domain is axisymmetric with b=1 while the other parameters are tan(α)=1, H=1 and ω=0.8.
Download Favier and Le Dizès supplementary movie 1(File)
File 9.7 MB
Supplementary material: File

Favier and Le Dizès supplementary movie 2

Trajectories of many particles randomly initialised within the volume. Each particle is travelling along the ray path at constant speed. Each particle is plotted as an empty symbol along with a line indicating past positions. The left panel shows top and side views while the right panel shows a 3D top view. The domain is non-axisymmetric with b=1.2 while the other parameters are tan(α)=1, H=1 and ω=0.8.
Download Favier and Le Dizès supplementary movie 2(File)
File 8.2 MB