Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bocanegra Evans, Humberto
Hamed, Ali M.
Gorumlu, Serdar
Doosttalab, Ali
Aksak, Burak
Chamorro, Leonardo P.
and
Castillo, Luciano
2018.
Engineered bio-inspired coating for passive flow control.
Proceedings of the National Academy of Sciences,
Vol. 115,
Issue. 6,
p.
1210.
Hamed, A. M.
and
Chamorro, L. P.
2018.
Turbulent boundary layer around 2D permeable and impermeable obstacles.
Experiments in Fluids,
Vol. 59,
Issue. 9,
Marjoribanks, T. I.
Lague, D.
Hardy, R. J.
Boothroyd, R. J.
Leroux, J.
Mony, C.
and
Puijalon, S.
2019.
Flexural Rigidity and Shoot Reconfiguration Determine Wake Length Behind Saltmarsh Vegetation Patches.
Journal of Geophysical Research: Earth Surface,
Vol. 124,
Issue. 8,
p.
2176.
ANJUM, Naveed
and
TANAKA, Norio
2019.
NUMERICAL MODELING OF THE TURBULENT FLOW STRUCTURE THROUGH VERTICALLY DOUBLE LAYER VEGETATION.
Journal of Japan Society of Civil Engineers, Ser. B1 (Hydraulic Engineering),
Vol. 75,
Issue. 2,
p.
I_487.
Zhou, Jian
and
Venayagamoorthy, Subhas K.
2019.
Near-field mean flow dynamics of a cylindrical canopy patch suspended in deep water.
Journal of Fluid Mechanics,
Vol. 858,
Issue. ,
p.
634.
Stevens, Craig
and
Plew, David
2019.
Bridging the Separation Between Studies of the Biophysics of Natural and Built Marine Canopies.
Frontiers in Marine Science,
Vol. 6,
Issue. ,
Chang, Wen-Yi
Constantinescu, George
and
Tsai, Whey-Fone
2020.
Effect of array submergence on flow and coherent structures through and around a circular array of rigid vertical cylinders.
Physics of Fluids,
Vol. 32,
Issue. 3,
Zhou, Jian
and
Venayagamoorthy, Subhas K.
2020.
How does three-dimensional canopy geometry affect the front propagation of a gravity current?.
Physics of Fluids,
Vol. 32,
Issue. 9,
Hamed, Ali M.
and
Peterlein, Adam M.
2020.
Turbulence structure of boundary layers perturbed by isolated and tandem roughness elements.
Journal of Turbulence,
Vol. 21,
Issue. 1,
p.
17.
Tinoco, Rafael O.
San Juan, Jorge E.
and
Mullarney, Julia C.
2020.
Simplification bias: lessons from laboratory and field experiments on flow through aquatic vegetation.
Earth Surface Processes and Landforms,
Vol. 45,
Issue. 1,
p.
121.
Anjum, Naveed
and
Tanaka, Norio
2020.
Investigating the turbulent flow behaviour through partially distributed discontinuous rigid vegetation in an open channel.
River Research and Applications,
Vol. 36,
Issue. 8,
p.
1701.
Hamed, Ali M.
Peterlein, Adam M.
and
Speck, Ian
2020.
Characteristics of the turbulent flow within short canopy gaps.
Physical Review Fluids,
Vol. 5,
Issue. 12,
Liu, W.
Lau, G. E.
and
Ngan, K.
2021.
Elucidating inhomogeneous scale-dependent flow statistics within regular obstacle arrays.
Physics of Fluids,
Vol. 33,
Issue. 10,
Chung, Hayoon
and
Koseff, Jeffrey
2021.
Turbulence structure and scales in canopy-wake reattachment.
Physical Review Fluids,
Vol. 6,
Issue. 11,
Cheng, Shyuan
Chamorro, Leonardo P.
and
Ansell, Phillip J.
2021.
On the H-type transition to turbulence—Laboratory experiments and reduced-order modeling.
Physics of Fluids,
Vol. 33,
Issue. 2,
Cai, Tengfei
Kim, Jin-Tae
Cheng, Shyuan
Ma, Fei
and
Chamorro, Leonardo P.
2021.
On the effect of orifice thickness and divergence angle in the near and intermediate fields of axisymmetric jets.
Experimental Thermal and Fluid Science,
Vol. 123,
Issue. ,
p.
110293.
Yoshida, Toshiya
and
Takemi, Tetsuya
2021.
Spatial characteristics of turbulent organized structures within the roughness sublayer over idealized urban surface with obstacle-height variability.
Environmental Fluid Mechanics,
Vol. 21,
Issue. 1,
p.
129.
Koken, Mete
and
Constantinescu, George
2021.
Flow structure inside and around a rectangular array of rigid emerged cylinders located at the sidewall of an open channel.
Journal of Fluid Mechanics,
Vol. 910,
Issue. ,
Houseago, Robert C.
Hong, Liu
Cheng, Shyuan
Best, James L.
Parsons, Daniel R.
and
Chamorro, Leonardo P.
2022.
On the turbulence dynamics induced by a surrogate seagrass canopy.
Journal of Fluid Mechanics,
Vol. 934,
Issue. ,
Li, Dian
Huai, Wenxin
Guo, Yakun
and
Liu, Mengyang
2022.
Flow characteristics in partially vegetated channel with homogeneous and heterogeneous layouts.
Environmental Science and Pollution Research,
Vol. 29,
Issue. 25,
p.
38186.
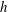 $h$ arranged in a staggered configuration; whereas the heterogeneous canopy resembled a row canopy and consisted of elements of two heights
$h$ arranged in a staggered configuration; whereas the heterogeneous canopy resembled a row canopy and consisted of elements of two heights 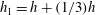 $h_{1}=h+(1/3)h$ and
$h_{1}=h+(1/3)h$ and 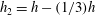 $h_{2}=h-(1/3)h$ alternated every two rows. Both canopies had the same density, element geometry and mean height. The flow was studied under three submergences
$h_{2}=h-(1/3)h$ alternated every two rows. Both canopies had the same density, element geometry and mean height. The flow was studied under three submergences 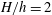 $H/h=2$, 3 and 4, where
$H/h=2$, 3 and 4, where 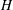 $H$ denotes the flow depth. The experiments were performed at Reynolds number
$H$ denotes the flow depth. The experiments were performed at Reynolds number 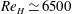 $Re_{H}\simeq 6500$, 11 300 and 12 300 and nearly constant Froude number
$Re_{H}\simeq 6500$, 11 300 and 12 300 and nearly constant Froude number 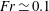 $Fr\simeq 0.1$. Turbulence statistics complemented with quadrant analysis and proper orthogonal decomposition reveal richer flow dynamics induced by height heterogeneity. Topography-induced spatially periodic mean flows are observed for the heterogeneous canopy. Furthermore, and in contrast to the homogeneous case, non-vanishing vertical velocity is maintained across the entire length of the heterogeneous canopy with increased levels at lower submergence depths. Further alternations were induced in the magnitude and distribution of the turbulent kinetic energy, Reynolds shear stress and characteristics of the canopy mixing layer, evidencing enhanced mixing and turbulent transport for the heterogeneous canopy especially at lower submergence depths. Overall, the results indicate that heterogeneous canopies exhibit greater vertical turbulent exchange at the canopy interface, suggesting a potential for greater scalar exchange and a greater impact on channel hydraulic resistance than a homogeneous canopy of similar roughness density.
$Fr\simeq 0.1$. Turbulence statistics complemented with quadrant analysis and proper orthogonal decomposition reveal richer flow dynamics induced by height heterogeneity. Topography-induced spatially periodic mean flows are observed for the heterogeneous canopy. Furthermore, and in contrast to the homogeneous case, non-vanishing vertical velocity is maintained across the entire length of the heterogeneous canopy with increased levels at lower submergence depths. Further alternations were induced in the magnitude and distribution of the turbulent kinetic energy, Reynolds shear stress and characteristics of the canopy mixing layer, evidencing enhanced mixing and turbulent transport for the heterogeneous canopy especially at lower submergence depths. Overall, the results indicate that heterogeneous canopies exhibit greater vertical turbulent exchange at the canopy interface, suggesting a potential for greater scalar exchange and a greater impact on channel hydraulic resistance than a homogeneous canopy of similar roughness density.