Hostname: page-component-7479d7b7d-wxhwt Total loading time: 0 Render date: 2024-07-08T09:03:28.988Z Has data issue: false hasContentIssue false
  • English
  • Français

A higher-order slender-body theory for axisymmetric flow past a particle at moderate Reynolds number

Published online by Cambridge University Press:  19 September 2018

Aditya S. Khair Open the ORCID record for Aditya S. Khair [Opens in a new window]  and
Nicholas G. Chisholm
Aditya S. Khair*
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Nicholas G. Chisholm
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
*
†Email address for correspondence: akhair@andrew.cmu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Slender-body theory is utilized to derive an asymptotic approximation to the hydrodynamic drag on an axisymmetric particle that is held fixed in an otherwise uniform stream of an incompressible Newtonian fluid at moderate Reynolds number. The Reynolds number, 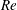$Re$, is based on the length of the particle. The axis of rotational symmetry of the particle is collinear with the uniform stream. The drag is expressed as a series in powers of 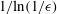$1/\text{ln}(1/\unicode[STIX]{x1D716})$, where $\unicode[STIX]{x1D716}$ is the small ratio of the characteristic width to length of the particle; the series is asymptotic for 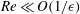$Re\ll O(1/\unicode[STIX]{x1D716})$. The drag is calculated through terms of 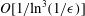$O[1/\text{ln}^{3}(1/\unicode[STIX]{x1D716})]$, thereby extending the work of Khayat & Cox (J. Fluid Mech., vol. 209, 1989, pp. 435–462) who determined the drag through 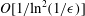$O[1/\text{ln}^{2}(1/\unicode[STIX]{x1D716})]$. The calculation of the 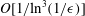$O[1/\text{ln}^{3}(1/\unicode[STIX]{x1D716})]$ term is accomplished via the generalized reciprocal theorem (Lovalenti & Brady, J. Fluid Mech., vol. 256, 1993, pp. 561–605). The first dependence of the inertial contribution to the drag on the cross-sectional profile of the particle is at 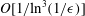$O[1/\text{ln}^{3}(1/\unicode[STIX]{x1D716})]$. Notably, the drag is insensitive to the direction of travel at this order. The asymptotic results are compared to a numerical solution of the Navier–Stokes equations for the case of a prolate spheroid. Good agreement between the two is observed at moderately small values of $\unicode[STIX]{x1D716}$, which is surprising given the logarithmic error associated with the asymptotic expansion.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Slender-body theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 421 - 444
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. & Taylor, T. D. 1962 Heat and mass transfer from single spheres in Stokes flow. Phys. Fluids 5, 387–394.Google Scholar
Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44, 419–440.Google Scholar
Brenner, H. 1961 The Oseen resistance of a particle of arbitrary shape. J. Fluid Mech. 11, 604–610.Google Scholar
Campion-Renson, A. & Crochet, M. J. 1978 On the stream function-vorticity finite element solutions of Navier–Stokes equations. Intl J. Numer. Meth. Engng 12, 1809–1818.Google Scholar
Carrier, G. F. 1953 On slow viscous flow. Final Report, Office of Naval Research Contract Nonr- 653 (00).Google Scholar
Chester, W. & Breach, D. R. 1969 On the flow past a sphere at low Reynolds number. J. Fluid Mech. 37, 751–760.Google Scholar
Chisholm, N. G., Lauga, E., Legendre, D. & Khair, A. S. 2016 A squirmer across Reynolds numbers. J. Fluid Mech. 30 (3), 375–382.Google Scholar
Chwang, A. T. & Wu, T. Y. 1976 Hydromechanics of low-Reynolds-number flow. Part 4. Translation of spheroids. J. Fluid Mech. 75, 677–689.Google Scholar
Cox, R. G. 1965 The steady motion of a particle of arbitrary shape at small Reynolds numbers. J. Fluid Mech. 23, 625–643.Google Scholar
Cox, R. G. 1970 The motion of long slender bodies in a viscous fluid. Part 1. General theory. J. Fluid Mech. 44, 791–810.Google Scholar
Dabade, V., Marath, N. K. & Subramanian, G. 2015 Effects of inertia and viscoelasticity on sedimenting anisotropic particles. J. Fluid Mech. 778, 133–188.Google Scholar
Happel, J. & Brenner, H. 1983 Low Reynolds Number Hydrodynamics. Martnius Nijhoff Publishers.Google Scholar
Hinch, E. J. 1991 Perturbation Methods. Cambridge University Press.Google Scholar
Homentcovshi, D. 1981 Axially symmetric Oseen flow past a slender body of revolution. SIAM J. Appl. Maths 40, 99–112.Google Scholar
Hormozi, S. & Ward, M. J. 2017 A hybrid asymptotic-numerical method for calculating drag coefficients in 2-D low Reynolds number flows. J. Engng Maths 102, 3–33.Google Scholar
Johnen, A., Remacle, J.-F. & Geuzaine, C. 2014 Geometric validity of high-order triangular finite elements. Engng Comput. 30 (3), 375–382.Google Scholar
Kaplun, S. & Lagerstrom, P. A. 1957 Asymptotic expansions of Navier–Stokes solutions for small Reynolds numbers. J. Math. Mech. 6, 585–593.Google Scholar
Karniadakis, G. & Sherwin, S. J. 2005 Spectral/hp Element Methods for Computational Fluid Dynamics, 2nd edn. Oxford University Press.Google Scholar
Khayat, M. C. A., Ward, M. J. & Keller, J. B. 1995 A hybrid asymptotic-numerical method for low Reynolds number flows past a cylindrical body. SIAM J. Appl. Maths 55, 1484–1510.Google Scholar
Khayat, R. E. & Cox, R. G. 1989 Inertia effects on the motion of long slender bodies. J. Fluid Mech. 209, 435–462.Google Scholar
Leal, L. G. 1975 The slow motion of slender rod-like particles in a second-order fluid. J. Fluid Mech. 69, 305–337.Google Scholar
Leal, L. G. 1980 Particle motions in a viscous fluid. Annu. Rev. Fluid Mech. 12, 435–476.Google Scholar
Lovalenti, P. M. & Brady, J. F. 1993 Hydrodynamic force on a rigid particle undergoing arbitrary time-dependent motion at small Reynolds number. J. Fluid Mech. 256, 561–605.Google Scholar
Olmstead, W. & Gautesen, A. 1968 A new paradox in viscous hydrodynamics. Arch. Rat. Mech. Anal. 29, 58–65.Google Scholar
Popescu, M. N., Dietrich, S., Tasinkevych, M. & Ralston, J. 2010 Phoretic motion of spheroidal particles due to self-generated solute gradients. Eur. Phys. J. E 31, 351–367.Google Scholar
Pozrikidis, C. 2001 Introduction to Theoretical and Computational Fluid Dynamics. Oxford University Press.Google Scholar
Proudman, I. & Pearson, J. R. A. 1957 Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder. J. Fluid Mech. 2, 237–262.Google Scholar
Relyea, L. M. & Khair, A. S. 2017 Forced convection heat and mass transfer from a slender particle. Chem. Engng Sci. 174, 285–289.Google Scholar
Romero, L. A. 1995 Forced convection past a slender body in a saturated porous medium. SIAM J. Appl. Maths 55, 975–985.Google Scholar
Roper, M. & Brenner, M. P. 2009 A nonperturbative approximation for the moderate Reynolds number Navier–Stokes equations. Proc. Natl Acad. Sci. 106, 2977–2982.Google Scholar
Roper, M., Squires, T. M. & Brenner, M. P. 2009 Symmetry unbreaking in the shapes of perfect projectiles. Phys. Fluids 20, 093606.Google Scholar
Schnitzer, O. 2015 Slender body approximations for advection-diffusion problems. J. Fluid Mech. 768, R5.Google Scholar
Schnitzer, O. & Yariv, E. 2015 Osmotic self-propulsion of slender particles. Phys. Fluids 27, 031701.Google Scholar
Shin, M., Subramanian, G. & Koch, D. L. 2006 A pseudospectral method to evaluate the fluid velocity produced by an array of translating slender fibers. Phys. Fluids 18, 063301.Google Scholar
Shin, M., Subramanian, G. & Koch, D. L. 2009 Structure and dynamics of dilute suspensions of finite-Reynolds-number settling fibers. Phys. Fluids 21, 123304.Google Scholar
Subramanian, G. & Koch, D. L. 2005 Inertial effects on fibre motion in simple shear flow. J. Fluid Mech. 535, 383–414.Google Scholar
Taylor, G. I. 1969 Motion of axisymmetric bodies in viscous fluids. In Problems of Hydrodynamics and Continuum Mechanics, pp. 718–724. SIAM Publications.Google Scholar
Tillett, J. P. K. 1970 Axial and transverse Stokes flow past slender axisymmetric bodies. J. Fluid Mech. 44, 401–417.Google Scholar
Veysey, J. I. & Goldenfeld, N. 2007 Simple viscous flows: from boundary layers to the renormalization group. Rev. Mod. Phys. 79, 883–927.Google Scholar