Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-21T14:04:23.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow-induced vibrations of a rotating cylinder in an arbitrary direction

Published online by Cambridge University Press:  11 December 2018

Rémi Bourguet Open the ORCID record for Rémi Bourguet [Opens in a new window]
Rémi Bourguet*
Affiliation:
Institut de Mécanique des Fluides de Toulouse, Université de Toulouse and CNRS, Toulouse, 31400, France
*
†Email address for correspondence: remi.bourguet@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow-induced vibrations of an elastically mounted circular cylinder, free to oscillate in an arbitrary direction and forced to rotate about its axis, are examined via two- and three-dimensional simulations, at a Reynolds number equal to 100, based on the body diameter and inflow velocity. The behaviour of the flow–structure system is investigated over the entire range of vibration directions, defined by the angle 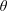$\unicode[STIX]{x1D703}$ between the direction of the current and the direction of motion, a wide range of values of the reduced velocity 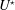$U^{\star }$ (inverse of the oscillator natural frequency) and three values of the rotation rate (ratio between the cylinder surface and inflow velocities), 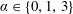$\unicode[STIX]{x1D6FC}\in \{0,1,3\}$, in order to cover the reference non-rotating cylinder case, as well as typical slow and fast rotation cases. The oscillations of the non-rotating cylinder (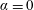$\unicode[STIX]{x1D6FC}=0$) develop under wake-body synchronization or lock-in, and their amplitude exhibits a bell-shaped evolution, typical of vortex-induced vibrations (VIV), as a function of 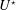$U^{\star }$. When 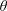$\unicode[STIX]{x1D703}$ is increased from 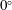$0^{\circ }$ to 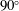$90^{\circ }$ (or decreased from 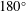$180^{\circ }$ to 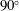$90^{\circ }$), the bell-shaped curve tends to monotonically increase in width and magnitude. For all angles, the flow past the non-rotating body is two-dimensional with formation of two counter-rotating spanwise vortices per cycle. The behaviour of the system remains globally the same for $\unicode[STIX]{x1D6FC}=1$. The principal effects of the slow rotation are a slight amplification of the VIV-like responses and widening of the vibration windows, as well as a limited asymmetry of the responses and forces about the symmetrical configuration 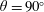$\unicode[STIX]{x1D703}=90^{\circ }$. The impact of the fast rotation (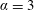$\unicode[STIX]{x1D6FC}=3$) is more pronounced: VIV-like responses persist over a range of 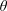$\unicode[STIX]{x1D703}$ but, outside this range, the system is found to undergo a transition towards galloping-like oscillations characterised by amplitudes growing unboundedly with 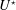$U^{\star }$. A quasi-steady modelling of fluid forcing predicts the emergence of galloping-like responses as 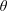$\unicode[STIX]{x1D703}$ is varied, which suggests that they could be mainly driven by the mean flow. It, however, appears that flow unsteadiness and body motion remain synchronised in this vibration regime where a variety of multi-vortex wake patterns are uncovered. The interaction with flow dynamics results in deviations from the quasi-steady prediction. The successive steps in the evolution of the vibration amplitude versus 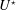$U^{\star }$, linked to wake pattern switch, are not captured by the quasi-steady approach. The flow past the rapidly-rotating, vibrating cylinder becomes three-dimensional over an interval of 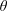$\unicode[STIX]{x1D703}$ including the in-line oscillation configuration, with only a minor effect on the system behaviour.

JFM classification

Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 860 , 10 February 2019 , pp. 739 - 766
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.Google Scholar
Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27, 648–658.Google Scholar
Bearman, P. W., Gartshore, I. S., Maull, D. J. & Parkinson, G. V. 1987 Experiments on flow-induced vibration of a square-section cylinder. J. Fluids Struct. 1, 19–34.Google Scholar
Bishop, R. E. D. & Hassan, A. Y. 1964 The lift and drag forces on a circular cylinder oscillating in a flowing fluid. Proc. R. Soc. Lond. A 277, 51–75.Google Scholar
Blevins, R. D. 1990 Flow-Induced Vibration. Van Nostrand Reinhold.Google Scholar
Bourguet, R. & Lo Jacono, D. 2014 Flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 740, 342–380.Google Scholar
Bourguet, R. & Lo Jacono, D. 2015 In-line flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 781, 127–165.Google Scholar
Brika, D. & Laneville, A. 1995 An experimental investigation of the aeolian vibrations of a flexible circular cylinder at different incidences. J. Fluids Struct. 9, 371–391.Google Scholar
Cagney, N. & Balabani, S. 2014 Streamwise vortex-induced vibrations of cylinders with one and two degrees of freedom. J. Fluid Mech. 758, 702–727.Google Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2001 Forces and wake modes of an oscillating cylinder. J. Fluids Struct. 15, 523–532.Google Scholar
Cetiner, O. & Rockwell, D. 2001 Streamwise oscillations of a cylinder in a steady current. Part 1. Locked-on states of vortex formation and loading. J. Fluid Mech. 427, 1–28.Google Scholar
Chew, Y. T., Cheng, M. & Luo, S. C. 1995 A numerical study of flow past a rotating circular cylinder using a hybrid vortex scheme. J. Fluid Mech. 299, 35–71.Google Scholar
Coutanceau, M. & Ménard, C. 1985 Influence of rotation on the near-wake development behind an impulsively started circular cylinder. J. Fluid Mech. 158, 399–446.Google Scholar
Dahl, J. M., Hover, F. S., Triantafyllou, M. S. & Oakley, O. H. 2010 Dual resonance in vortex-induced vibrations at subcritical and supercritical Reynolds numbers. J. Fluid Mech. 643, 395–424.Google Scholar
Den Hartog, J. P. 1932 Transmission line vibration due to sleet. Trans. Am. Inst. Electr. Engrs 51, 1074–1076.Google Scholar
El Akoury, R., Braza, M., Perrin, R., Harran, G. & Hoarau, Y. 2008 The three-dimensional transition in the flow around a rotating cylinder. J. Fluid Mech. 607, 1–11.Google Scholar
Gsell, S., Bourguet, R. & Braza, M. 2016 Two-degree-of-freedom vortex-induced vibrations of a circular cylinder at Re = 3900. J. Fluids Struct. 67, 156–172.Google Scholar
Kang, S., Choi, H. & Lee, S. 1999 Laminar flow past a rotating circular cylinder. Phys. Fluids 11, 3312–3321.Google Scholar
Karniadakis, G. E. & Sherwin, S. 1999 Spectral/hp Element Methods for CFD, 1st edn. Oxford University Press.Google Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13, 813–851.Google Scholar
Konstantinidis, E. 2014 On the response and wake modes of a cylinder undergoing streamwise vortex-induced vibration. J. Fluids Struct. 45, 256–262.Google Scholar
Leontini, J. S., Stewart, B. E., Thompson, M. C. & Hourigan, K. 2006 Wake state and energy transitions of an oscillating cylinder at low Reynolds number. Phys. Fluids 18, 067101.Google Scholar
Mannini, C., Marra, A. M. & Bartoli, G. 2014 VIV-galloping instability of rectangular cylinders: review and new experiments. J. Wind Engng Ind. Aerodyn. 132, 109–124.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.Google Scholar
Mittal, S. & Tezduyar, T. E. 1992 A finite element study of incompressible flows past oscillating cylinders and aerofoils. Intl J. Numer. Meth. Fluids 15, 1073–1118.Google Scholar
Mukhopadhyay, V. & Dugundji, J. 1976 Wind excited vibration of a square section cantilever beam in smooth flow. J. Sound Vib. 45, 329–339.Google Scholar
Nakamura, Y. & Tomonari, Y. 1977 Galloping of rectangular prisms in a smooth and a turbulent flow. J. Sound Vib. 52, 233–241.Google Scholar
Naudascher, E. & Rockwell, D. 1994 Flow-Induced Vibrations: An Engineering Guide. Dover.Google Scholar
Navrose & Mittal, S. 2016 Lock-in in vortex-induced vibration. J. Fluid Mech. 794, 565–594.Google Scholar
Nemes, A., Zhao, J., Lo Jacono, D. & Sheridan, J. 2012 The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack. J. Fluid Mech. 710, 102–130.Google Scholar
Obasaju, E. D., Ermshaus, R. & Naudascher, E. 1990 Vortex-induced streamwise oscillations of a square-section cylinder in a uniform stream. J. Fluid Mech. 213, 171–189.Google Scholar
Okajima, A., Ohtsuyama, S., Nagamori, T., Nakano, T. & Kiwata, T. 1999 In-line oscillation of structure with a circular or rectangular section. Trans. Japan Soc. Mech. Engng 65, 2196–2203.Google Scholar
Ongoren, A. & Rockwell, D. 1988 Flow structure from an oscillating cylinder. Part 2. Mode competition in the near wake. J. Fluid Mech. 191, 225–245.Google Scholar
Païdoussis, M. P., Price, S. J. & de Langre, E. 2010 Fluid–Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.Google Scholar
Parkinson, G. V. & Smith, J. D. 1964 The square prism as an aeroelastic nonlinear oscillator. Q. J. Mech. Appl. Maths 17, 225–239.Google Scholar
Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.Google Scholar
Pralits, J. O., Giannetti, F. & Brandt, L. 2013 Three-dimensional instability of the flow around a rotating circular cylinder. J. Fluid Mech. 730, 5–18.Google Scholar
Prandtl, L.1925 Application of the ‘Magnus effect’ to the wind propulsion of ships. Die Naturwissenschaft 13, 93108 – NACA Tech. Mem. 367 13, 93–108.Google Scholar
Rao, A., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2013 Three-dimensionality in the wake of a rapidly rotating cylinder in uniform flow. J. Fluid Mech. 730, 379–391.Google Scholar
Rao, A., Radi, A., Leontini, J. S., Thompson, M. C., Sheridan, J. & Hourigan, K. 2015 A review of rotating cylinder wake transitions. J. Fluids Struct. 53, 2–14.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19, 389–447.Google Scholar
Seyed-Aghazadeh, B. & Modarres-Sadeghi, Y. 2015 An experimental investigation of vortex-induced vibration of a rotating circular cylinder in the crossflow direction. Phys. Fluids 27, 067101.Google Scholar
Stansby, P. K. & Rainey, R. C. T. 2001 On the orbital response of a rotating cylinder in a current. J. Fluid Mech. 439, 87–108.Google Scholar
Stojković, D., Breuer, M. & Durst, F. 2002 Effect of high rotation rates on the laminar flow around a circular cylinder. Phys. Fluids 14, 3160–3178.Google Scholar
Wang, X. Q., So, R. M. C. & Chan, K. T. 2003 A non-linear fluid force model for vortex-induced vibration of an elastic cylinder. J. Sound Vib. 260, 287–305.Google Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–538.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.Google Scholar
Wong, K. W. L., Zhao, J., Lo Jacono, D., Thompson, M. C. & Sheridan, J. 2017 Experimental investigation of flow-induced vibration of a rotating circular cylinder. J. Fluid Mech. 829, 486–511.Google Scholar
Wu, X., Ge, F. & Hong, Y. 2012 A review of recent studies on vortex-induced vibrations of long slender cylinders. J. Fluids Struct. 28, 292–308.Google Scholar
Yogeswaran, V. & Mittal, S. 2011 Vortex-induced and galloping response of a rotating circular cylinder. In IUTAM Symposium on Bluff Body Flows, IIT-Kanpur, India (ed. Mittal, S. & Biswas, G.), pp. 153–156.Google Scholar
Zhao, J., Leontini, J. S., Lo Jacono, D. & Sheridan, J. 2014a Fluid–structure interaction of a square cylinder at different angles of attack. J. Fluid Mech. 747, 688–721.Google Scholar
Zhao, M., Cheng, L. & Lu, L. 2014b Vortex induced vibrations of a rotating circular cylinder at low Reynolds number. Phys. Fluids 26, 073602.Google Scholar
Zhao, M., Cheng, L. & Zhou, T. 2013 Numerical simulation of vortex-induced vibration of a square cylinder at a low Reynolds number. Phys. Fluids 25, 023603.Google Scholar