Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-16T17:29:44.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow dynamics in sinusoidal channels at moderate Reynolds numbers

Published online by Cambridge University Press:  29 September 2023

S.W. Gepner Open the ORCID record for S.W. Gepner [Opens in a new window]  and
J.M. Floryan Open the ORCID record for J.M. Floryan [Opens in a new window]
S.W. Gepner*
Affiliation:
Institute of Aeronautics and Applied Mechanics, Warsaw University of Technology, Nowowiejska 24, 00-665 Warsaw, Poland
J.M. Floryan
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario N6A 5B9, Canada
*
†Email address for correspondence: stanislaw.gepner@pw.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

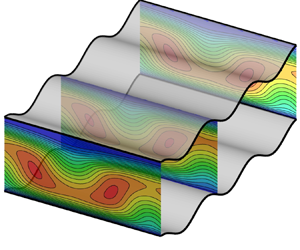
Pressure-gradient-driven flows through sinusoidal channels have been studied. The analysis was carried out up to the formation of secondary nonlinear states and spanned a range of low and moderate Reynolds numbers. Direct numerical simulations were used to identify and determine the properties of steady as well as non-stationary, two-dimensional (2-D) and three-dimensional secondary flows. Our results indicate the existence of several distinct solution types. Two-dimensional, stationary flows with periodicity determined by the corrugation represent the first type. The second type is associated with the appearance of 2-D oscillatory flows arising from the onset of unstable travelling waves. Such oscillatory solutions are generally out of phase with the wall corrugation but could be in phase in special cases determined by the ratio of the critical disturbance wavelength and the channel corrugation wavelength. Consequently, several distinct types of time-dependent solutions are possible. The third type of solution results from the centrifugal effect caused by wall curvature and leads to three-dimensionalization of the flow through the onset of stationary streamwise vortices. Finally, various states resulting from the interaction of different solution types are possible. We examine those states and present a bifurcation diagram illustrating the formation of some of them. The results presented in this paper might help with the development of small-scale flow measurement and detection devices operating at low and moderate Reynolds numbers, as well as in the use of wall topographies for the intensification of mixing in flows with moderate, subturbulent Reynolds numbers.

JFM classification

Flow Control: Instability control
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 972 , 10 October 2023 , A22
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asai, M. & Floryan, J.M. 2006 Experiments on the linear instability of flow in a wavy channel. Eur. J. Mech. (B/Fluids) 25 (6), 971–986.CrossRefGoogle Scholar
Blancher, S., Creff, R. & Le Quere, P. 1998 Effect of Tollmien Schlichting wave on convective heat transfer in a wavy channel. Part I. Linear analysis. Intl J. Heat Fluid Flow 19 (1), 39–48.CrossRefGoogle Scholar
Blancher, S., Le Guer, Y. & El Omari, K. 2015 Spatio-temporal structure of the ‘fully developed’ transitional flow in a symmetric wavy channel. Linear and weakly nonlinear stability analysis. J. Fluid Mech. 764, 250–276.CrossRefGoogle Scholar
Cabal, A., Szumbarski, J. & Floryan, J.M. 2002 Stability of flow in a wavy channel. J. Fluid Mech. 457, 191–212.CrossRefGoogle Scholar
Cantwell, C.D., et al. 2015 Nektar++: an open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219.CrossRefGoogle Scholar
Cantwell, C.D., Sherwin, S.J., Kirby, R.M. & Kelly, P.H.J. 2011 From h to p efficiently: strategy selection for operator evaluation on hexahedral and tetrahedral elements. Comput. Fluids. 43 (1), 23–28.CrossRefGoogle Scholar
Cho, K.J., Kim, M.-U. & Shin, H.D. 1998 Linear stability of two-dimensional steady flow in wavy-walled channels. Fluid Dyn. Res. 23 (6), 349–370.CrossRefGoogle Scholar
Floryan, J.M. 1997 Stability of wall-bounded shear layers in the presence of simulated distributed surface roughness. J. Fluid Mech. 335, 29–55.CrossRefGoogle Scholar
Floryan, J.M. 2002 Centrifugal instability of Couette flow over a wavy wall. Phys. Fluids 14 (1), 312–322.CrossRefGoogle Scholar
Floryan, J.M. 2003 a Vortex instability in a diverging–converging channel. J. Fluid Mech. 482, 17–50.CrossRefGoogle Scholar
Floryan, J.M. 2003 b Wall-transpiration-induced instabilities in plane Couette flow. J. Fluid Mech. 488, 151–188.CrossRefGoogle Scholar
Floryan, J.M. 2005 Two-dimensional instability of flow in a rough channel. Phys. Fluids 17 (4), 044101.CrossRefGoogle Scholar
Floryan, J.M. 2007 Three-dimensional instabilities of laminar flow in a rough channel and the concept of hydraulically smooth wall. Eur. J. Mech. (B/Fluids) 26 (3), 305–329.CrossRefGoogle Scholar
Floryan, J.M. 2015 Flow in a meandering channel. J. Fluid Mech. 770, 52–84.CrossRefGoogle Scholar
Floryan, J.M. & Asai, M. 2011 On the transition between distributed and isolated surface roughness and its effect on the stability of channel flow. Phys. Fluids 23 (10), 104101.CrossRefGoogle Scholar
Floryan, J.M. & Floryan, C. 2010 Traveling wave instability in a diverging-converging channel. Fluid Dyn. Res. 42 (2), 025509.CrossRefGoogle Scholar
Gepner, S.W. & Floryan, J.M. 2016 Flow dynamics and enhanced mixing in a converging–diverging channel. J. Fluid Mech. 807, 167–204.CrossRefGoogle Scholar
Gepner, S.W. & Floryan, J.M. 2020 Use of surface corrugations for energy-efficient chaotic stirring in low Reynolds number flows. Sci. Rep. 10, 9865.CrossRefGoogle ScholarPubMed
Gepner, S.W., Yadav, N. & Szumbarski, J. 2020 Secondary flows in a longitudinally grooved channel and enhancement of diffusive transport. Intl J. Heat Mass Transfer 153, 119523.CrossRefGoogle Scholar
Geuzaine, C. & Remacle, J.-F. 2009 Gmsh: a 3-D finite element mesh generator with built-in pre- and post-processing facilities. Intl J. Numer. Meth. Engng 79 (11), 1309–1331.CrossRefGoogle Scholar
Gschwind, P., Regele, A. & Kottke, V. 1995 Sinusoidal wavy channels with Taylor–Görtler vortices. Exp. Therm. Fluid Sci. 11 (3), 270.CrossRefGoogle Scholar
Guermond, J.-L. & Shen, J. 2003 Velocity-correction projection methods for incompressible flows. SIAM J. Numer. Anal. 41 (1), 112–134.CrossRefGoogle Scholar
Guzmn, A.M. & Amon, C.H. 1994 Transition to chaos in converging-diverging channel flows: Ruelle–Takens–Newhouse scenario. Phys. Fluids 6 (6), 1994–2002.CrossRefGoogle Scholar
Guzmn, A.M. & Amon, C.H. 1996 Dynamical flow characterization of transitional and chaotic regimes in converging-diverging channels. J. Fluid Mech. 321, 25–57.CrossRefGoogle Scholar
Husain, S.Z., Floryan, J.M. & Szumbarski, J. 2009 Over-determined formulation of the immersed boundary conditions method. Comput. Meth. Appl. Mech. Engng 199 (1–4), 94–112.CrossRefGoogle Scholar
Karniadakis, G. & Sherwin, S. 2013 Spectral/hp Element Methods for Computational Fluid Dynamics. Oxford University Press.Google Scholar
Lee, H.J., Sherrit, S., Tosi, L.P., Walkemeyer, P. & Colonius, T. 2015 Piezoelectric energy harvesting in internal fluid flow. Sensors 15 (10), 26039–26062.CrossRefGoogle ScholarPubMed
Lehoucq, R. & Sorensen, D. 1997 ARPACK: Solution of large scale eigenvalue problems with implicitly restarted Arnoldi methods. User's guide. Available at: http://www.caam.rice.edu/software/arpack.Google Scholar
Mitsudharmadi, H., Jamaludin, M.N.A. & Winoto, S.H. 2012 Streamwise vortices in channel flow with a corrugated surface. Proceedings of the 10th WSEAS International Conference on Fluid Mechanics & Aerodynamics (FMA’12), Istanbul, Turkey.Google Scholar
Mohammadi, A. & Floryan, J.M. 2012 Mechanism of drag generation by surface corrugation. Phys. Fluids 24 (1), 013602.CrossRefGoogle Scholar
Mohammadi, A. & Floryan, J.M. 2013 Pressure losses in grooved channels. J. Fluid Mech. 725, 23–54.CrossRefGoogle Scholar
Mohammadi, A., Moradi, H.V. & Floryan, J.M. 2015 New instability mode in a grooved channel. J. Fluid Mech. 778, 691–720.CrossRefGoogle Scholar
Mohammadi, M. & Floryan, J.M. 2010 Pressures losses in grooved channels. In APS Division of Fluid Dynamics Meeting Abstracts, vol. 63, pp. LY–007.Google Scholar
Moradi, H.V. & Floryan, J.M. 2014 Stability of flow in a channel with longitudinal grooves. J. Fluid Mech. 757, 613–648.CrossRefGoogle Scholar
Moxey, D., Cantwell, C.D., Bao, Y., Cassinelli, A., Castiglioni, G., Chun, S., Juda, E., Kazemi, E., Lackhove, K., Marcon, J., et al. 2019 Nektar++: enhancing the capability and application of high-fidelity spectral/hp element methods. arXiv:1906.03489.Google Scholar
Nishimura, T., Murakami, S., Arakawa, S. & Kawamura, Y. 1990 a Flow observations and mass transfer characteristics in symmetrical wavy-walled channels at moderate Reynolds numbers for steady flow. Intl J. Heat Mass Transfer 33 (5), 835–845.Google Scholar
Nishimura, T., Ohori, Y., Kajimoto, Y. & Kawamura, Y. 1985 Mass transfer characteristics in a channel with symmetric wavy wall for steady flow. J. Chem. Engng Japan 18 (6), 550–555.CrossRefGoogle Scholar
Nishimura, T., Ohori, Y. & Kawamura, Y. 1984 Flow characteristics in a channel with symmetric wavy wall for steady flow. J. Chem. Engng Japan 17 (5), 466–471.CrossRefGoogle Scholar
Nishimura, T., Yano, K., Yoshino, T. & Kawamura, Y. 1990 b Occurrence and structure of Taylor–Görtler vortices induced in two-dimensional wavy channels for steady flow. J. Chem. Engng Japan 23 (6), 697–703.CrossRefGoogle Scholar
Pushenko, V. & Gepner, S.W. 2021 Flow destabilization and nonlinear solutions in low aspect ratio, corrugated duct flows. Phys. Fluids 33 (4), 044109.CrossRefGoogle Scholar
Ralph, M.E. 1986 Oscillatory flows in wavy-walled tubes. J. Fluid Mech. 168, 515–540.CrossRefGoogle Scholar
Rivera-Alvarez, A. & Ordonez, J.C. 2013 Global stability of flow in symmetric wavy channels. J. Fluid Mech. 733, 625–649.CrossRefGoogle Scholar
Sobey, I.J. 1980 On flow through furrowed channels. Part 1. Calculated flow patterns. J. Fluid Mech. 96, 1–26.CrossRefGoogle Scholar
Stephanoff, K.D., Sobey, I.J. & Bellhouse, B.J. 1980 On flow through furrowed channels. Part 2. Observed flow patterns. J. Fluid Mech. 96 (1), 27–32.CrossRefGoogle Scholar
Szumbarski, J. 2002 a Immersed boundary approach to stability equations for a spatially periodic viscous flow. Arch. Mech. 54 (3), 199–222.Google Scholar
Szumbarski, J. 2002 b On origin of unstable modes in viscous channel flow subject to periodically distributed surface suction. J. Theor. Appl. Mech. 40 (4), 847–871.Google Scholar
Szumbarski, J. 2007 Instability of viscous incompressible flow in a channel with transversely corrugated walls. J. Theor. Appl. Mech. 45 (3), 659–683.Google Scholar
Szumbarski, J. & Błoñski, S. 2011 Destabilization of a laminar flow in a rectangular channel by transversely-oriented wall corrugation. Arch. Mech. 63 (4), 393–428.Google Scholar
Szumbarski, J., Blonski, S. & Kowalewski, T. 2011 Impact of transversely-oriented wall corrugation on hydraulic resistance of a channel flow. Arch. Mech. Engng 58 (4), 441.Google Scholar
Wang, C.-C. & Chen, C.-K. 2002 Forced convection in a wavy-wall channel. Intl J. Heat Mass Transfer 45 (12), 2587–2595.CrossRefGoogle Scholar
Wang, G. & Vanka, S.P. 1995 Convective heat transfer in periodic wavy passages. Intl J. Heat Mass Transfer 38 (17), 3219–3230.CrossRefGoogle Scholar
Xu, H., Cantwell, C., Monteserin, C., Eskilsson, C., Engsig-Karup, A. & Sherwin, S. 2018 Spectral/hp element methods: recent developments, applications, and perspectives. J. Hydrodyn. 30, 1–22.CrossRefGoogle Scholar
Yadav, N., Gepner, S.W. & Szumbarski, J. 2017 Instability in a channel with grooves parallel to the flow. Phys. Fluids 29 (8), 084104.CrossRefGoogle Scholar
Yadav, N., Gepner, S.W. & Szumbarski, J. 2018 Flow dynamics in longitudinally grooved duct. Phys. Fluids 30 (10), 104105.CrossRefGoogle Scholar
Yadav, N., Gepner, S.W. & Szumbarski, J. 2021 Determination of groove shape with strong destabilization and low hydraulic drag. Intl J. Heat Fluid Flow 87, 108751.CrossRefGoogle Scholar