Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-07-05T12:05:37.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Extreme vortex states and the growth of enstrophy in three-dimensional incompressible flows

Published online by Cambridge University Press:  06 April 2017

Diego Ayala  and
Bartosz Protas Open the ORCID record for Bartosz Protas [Opens in a new window]
Diego Ayala
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA Department of Mathematics and Statistics, McMaster University, Hamilton, Ontario, L8S 4K1, Canada
Bartosz Protas*
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton, Ontario, L8S 4K1, Canada
*
†Email address for correspondence: bprotas@mcmaster.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

In this investigation we study extreme vortex states defined as incompressible velocity fields with prescribed enstrophy 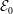${\mathcal{E}}_{0}$ which maximize the instantaneous rate of growth of enstrophy $\text{d}{\mathcal{E}}/\text{d}t$. We provide an analytic characterization of these extreme vortex states in the limit of vanishing enstrophy ${\mathcal{E}}_{0}$ and, in particular, show that the Taylor–Green vortex is in fact a local maximizer of $\text{d}{\mathcal{E}}/\text{d}t$ in this limit. For finite values of enstrophy, the extreme vortex states are computed numerically by solving a constrained variational optimization problem using a suitable gradient method. In combination with a continuation approach, this allows us to construct an entire family of maximizing vortex states parameterized by their enstrophy. We also confirm the findings of the seminal study by Lu & Doering (Indiana Univ. Math. J., vol. 57, 2008, pp. 2693–2727) that these extreme vortex states saturate (up to a numerical prefactor) the fundamental bound $\text{d}{\mathcal{E}}/\text{d}t<C{\mathcal{E}}^{3}$, for some constant 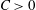$C>0$. The time evolution corresponding to these extreme vortex states leads to a larger growth of enstrophy than the growth achieved by any of the commonly used initial conditions with the same enstrophy ${\mathcal{E}}_{0}$. However, based on several different diagnostics, there is no evidence of any tendency towards singularity formation in finite time. Finally, we discuss possible physical reasons why the initially large growth of enstrophy is not sustained for longer times.

JFM classification

Mathematical Foundations: Variational methods Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , pp. 772 - 806
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, R. A. & Fournier, J. F. 2005 Sobolev Spaces. Elsevier.Google Scholar
Ayala, D.2014 Extreme vortex states and singularity formation in incompressible flows. PhD thesis, McMaster University, available at http://hdl.handle.net/11375/15453.Google Scholar
Ayala, D. & Doering, C. R.2016 Extreme enstrophy growth in axisymmetric flows (in preparation).Google Scholar
Ayala, D., Doering, C. R. & Simon, T. S.2016 Sharp bounds for the maximum growth of palinstrophy in two-dimensional incompressible flows (in preparation).Google Scholar
Ayala, D. & Protas, B. 2011 On maximum enstrophy growth in a hydrodynamic system. Physica D 240, 1553–1563.Google Scholar
Ayala, D. & Protas, B. 2014a Maximum palinstrophy growth in 2D incompressible flows. J. Fluid Mech. 742, 340–367.Google Scholar
Ayala, D. & Protas, B. 2014b Vortices, maximum growth and the problem of finite-time singularity formation. Fluid Dyn. Res. 46 (3), 031404.Google Scholar
Bewley, T. R. 2009 Numerical Renaissance. Renaissance Press.Google Scholar
Boratav, O. N. & Pelz, R. B. 1994 Direct numerical simulation of transition to turbulence from a high-symmetry initial condition. Phys. Fluids 6, 2757–2784.Google Scholar
Brachet, M. E. 1991 Direct simulation of three-dimensional turbulence in the Taylor–Green vortex. Fluid Dyn. Res. 8, 1–8.CrossRefGoogle Scholar
Brachet, M. E., Meiron, D. I., Orszag, S. A., Nickel, B. G., Morf, R. H. & Frisch, U. 1983 Small-scale structure of the Taylor–Green vortex. J. Fluid Mech. 130, 411–452.Google Scholar
Bustamante, M. D. & Brachet, M. 2012 Interplay between the Beale–Kato–Majda theorem and the analyticity-strip method to investigate numerically the incompressible Euler singularity problem. Phys. Rev. E 86, 066302.Google Scholar
Bustamante, M. D. & Kerr, R. M. 2008 3D Euler about a 2D symmetry plane. Physica D 237, 1912–1920.Google Scholar
Caffarelli, L., Kohn, R. & Nirenberg, L. 1983 Partial regularity of suitable weak solutions of the Navier–Stokes equations. Commun. Pure Appl. Maths 35, 771–831.Google Scholar
Cichowlas, C. & Brachet, M. E. 2005 Evolution of complex singularities in Kida–Pelz and Taylor–Green inviscid flows. Fluid Dyn. Res. 36, 239–248.Google Scholar
Davidson, P. A. 2004 Turbulence. In An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Doering, C. R. 2009 The 3D Navier–Stokes problem. Annu. Rev. Fluid Mech. 41, 109–128.Google Scholar
Doering, C. R. & Gibbon, J. D. 1995 Applied Analysis of the Navier–Stokes Equations. Cambridge University Press.Google Scholar
Dombre, T., Frisch, U., Greene, J. M., Hénon, M., Mehr, A. & Soward, A. M. 1986 Chaotic streamlines in the ABC flows. J. Fluid Mech. 167, 353–391.Google Scholar
Donzis, D. A., Gibbon, J. D., Gupta, A., Kerr, R. M., Pandit, R. & Vincenzi, D. 2013 Vorticity moments in four numerical simulations of the 3D Navier–Stokes equations. J. Fluid Mech. 732, 316–331.Google Scholar
Fefferman, C. L.2000 Existence and smoothness of the Navier–Stokes equation. Available at http://www.claymath.org/millennium/Navier–Stokes_Equations/navierstokes.pdf, Clay Millennium Prize Problem Description.Google Scholar
Foias, C. & Temam, R. 1989 Gevrey class regularity for the solutions of the Navier–Stokes equations. J. Funct. Anal. 87, 359–369.Google Scholar
Frigo, M. & Johnson, S. G. 2003 FFTW User’s Manual. Massachusetts Institute of Technology.Google Scholar
Gibbon, J. D., Donzis, D., Gupta, A., Kerr, R. M., Pandit, R. & Vincenzi, D. 2014 Regimes of nonlinear depletion and regularity in the 3D Navier–Stokes equations. Nonlinearity 27, 1–19.Google Scholar
Gibbon, J. D., Bustamante, M. & Kerr, R. M. 2008 The three–dimensional Euler equations: singular or non–singular? Nonlinearity 21, 123–129.Google Scholar
Grafke, T., Homann, H., Dreher, J. & Grauer, R. 2008 Numerical simulations of possible finite-time singularities in the incompressible Euler equations: comparison of numerical methods. Physica D 237, 1932–1936.Google Scholar
Gunzburger, M. D. 2003 Perspectives in Flow Control and Optimization. SIAM.Google Scholar
Hou, T. Y. 2009 Blow-up or no blow-up? a unified computational and analytic approach to 3D incompressible Euler and Navier–Stokes equations. Acta Numerica 18, 277–346.Google Scholar
Hou, T. Y. & Li, R. 2007 Computing nearly singular solutions using pseudo-spectral methods. J. Comput. Phys. 226, 379–397.Google Scholar
Kerr, R. M. 1993 Evidence for a singularity of the three-dimensional, incompressible Euler equations. Phys. Fluids A 5, 1725–1746.Google Scholar
Kerr, R. M. 2013a Bounds for Euler from vorticity moments and line divergence. J. Fluid Mech. 729, R2.Google Scholar
Kerr, R. M. 2013b Swirling, turbulent vortex rings formed from a chain reaction of reconnection events. Phys. Fluids 25, 065101.Google Scholar
Kim, N. 2003 Remarks for the axisymmetric Navier–Stokes equations. J. Differ. Equ. 187, 226–239.Google Scholar
Kiselev, A. 2010 Regularity and blow up for active scalars. Math. Model. Nat. Phenom. 5, 225–255.Google Scholar
Kreiss, H. & Lorenz, J. 2004 Initial-Boundary Value Problems and the Navier–Stokes Equations, Classics in Applied Mathematics, vol. 47. SIAM.Google Scholar
Ladyzhenskaya, O. A. 1969 The Mathematical Theory of Viscous Incompressible Flow. Gordon and Breach.Google Scholar
Lu, L.2006 Bounds on the enstrophy growth rate for solutions of the 3D Navier–Stokes equations. PhD thesis, University of Michigan.Google Scholar
Lu, L. & Doering, C. R. 2008 Limits on enstrophy growth for solutions of the three-dimensional Navier–Stokes equations. Indiana Univ. Math. J. 57, 2693–2727.CrossRefGoogle Scholar
Luenberger, D. 1969 Optimization by Vector Space Methods. Wiley.Google Scholar
Luo, G. & Hou, T. Y. 2014a Potentially singular solutions of the 3D axisymmetric Euler equations. Proc. Natl Acad. Sci. USA 111 (36), 12968–12973.Google Scholar
Luo, G. & Hou, T. Y. 2014b Toward the finite-time blowup of the 3D incompressible Euler equations: a numerical investigation. SIAM Multiscale Model. Simul. 12 (4), 1722–1776.Google Scholar
Majda, A. J. & Bertozzi, A. L. 2002 Vorticity and Incompressible Flow. Cambridge University Press.Google Scholar
Matsumoto, T., Bec, J. & Frisch, U. 2008 Complex-space singularities of 2D Euler flow in lagrangian coordinates. Physica D 237, 1951–1955.Google Scholar
Miettinen, K. 1999 Nonlinear Multiobjective Optimization. Springer.Google Scholar
Ohkitani, K. 2008 A miscellany of basic issues on incompressible fluid equations. Nonlinearity 21, 255–271.CrossRefGoogle Scholar
Ohkitani, K. & Constantin, P. 2008 Numerical study of the Eulerian–Lagrangian analysis of the Navier–Stokes turbulence. Phys. Fluids 20, 1–11.Google Scholar
Orlandi, P., Pirozzoli, S., Bernardini, M. & Carnevale, G. F. 2014 A minimal flow unit for the study of turbulence with passive scalars. J. Turbul. 15, 731–751.Google Scholar
Orlandi, P., Pirozzoli, S. & Carnevale, G. F. 2012 Vortex events in Euler and Navier–Stokes simulations with smooth initial conditions. J. Fluid Mech. 690, 288–320.Google Scholar
Pelz, R. B. 2001 Symmetry and the hydrodynamic blow-up problem. J. Fluid Mech. 444, 299–320.Google Scholar
Protas, B., Bewley, T. & Hagen, G. 2004 A comprehensive framework for the regularization of adjoint analysis in multiscale PDE systems. J. Comput. Phys. 195, 49–89.Google Scholar
Pumir, A. & Siggia, E. 1990 Collapsing solutions to the 3D Euler equations. Phys. Fluids A 2, 220–241.Google Scholar
Ruszczyński, A. 2006 Nonlinear Optimization. Princeton University Press.Google Scholar
Siegel, M. & Caflisch, R. E. 2009 Calculation of complex singular solutions to the 3D incompressible Euler equations. Physica D 238, 2368–2379.Google Scholar
Taylor, G. I. & Green, A. E. 1937 Mechanism of the production of small eddies from large ones. Proc. R. Soc. Lond. A 158, 499–521.Google Scholar