Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-15T19:36:53.943Z Has data issue: false hasContentIssue false
  • English
  • Français

Eigenvalue bounds for compressible stratified magnetoshear flows varying in two transverse directions

Published online by Cambridge University Press:  17 June 2021

Kengo Deguchi Open the ORCID record for Kengo Deguchi [Opens in a new window]
Kengo Deguchi*
Affiliation:
School of Mathematics, Monash University, VIC3800, Australia
*
†Email address for correspondence: kengo.deguchi@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

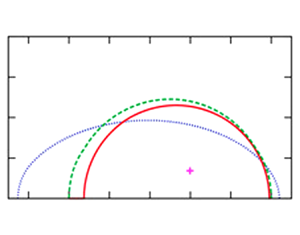
Three eigenvalue bounds are derived for the instability of ideal compressible stratified magnetohydrodynamic shear flows in which the base velocity, density and magnetic field vary in two directions. The first bound can be obtained by combining the Howard semicircle theorem with the energy principle of the Lagrangian displacement. Remarkably, no special conditions are needed to use this bound, and for some cases, we can establish the stability of the flow. The second and third bounds come out from a generalisation of the Miles–Howard theory and have some similarity to the semi-ellipse theorem by Kochar & Jain (J. Fluid Mech., vol. 91, 1979, p. 489) and the bound found by Cally (Astrophys. Fluid Dyn., vol. 31, 1983, p. 43), respectively. An important byproduct of this investigation is that the Miles–Howard stability condition holds only when there is no applied magnetic field and, in addition, the directions of the shear and the stratification are aligned everywhere.

JFM classification

Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 920 , 10 August 2021 , A55
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adam, J.A. 1978 a Stability of aligned magnetoatmospheric flow. J. Plasma Phys. 19, 77–86.CrossRefGoogle Scholar
Adam, J.A. 1978 b Magnetohydrodynamic wave energy flux in a stratified compressible atmosphere with shear. Q. J. Mech. Appl. Maths 31, 77–98.CrossRefGoogle Scholar
Alizard, F. 2015 Linear stability of optimal streaks in the log-layer of turbulent channel flows. Phys. Fluids 27, 105103.CrossRefGoogle Scholar
Andersson, P., Brandt, L., Bottaro, A. & Henningson, D.S. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.CrossRefGoogle Scholar
Arnold, V.I. 1978 Mathematical Methods of Classical Mechanics. Springer.CrossRefGoogle Scholar
Beaume, C., Chini, G.P., Julien, K. & Knobloch, E. 2015 Reduced description of exact coherent states in parallel shear flows. Phys. Rev. E 91, 024003.CrossRefGoogle ScholarPubMed
Benney, D. 1984 The evolution of disturbances in shear flows at high Reynolds numbers. Stud. Appl. Maths 70, 1–19.CrossRefGoogle Scholar
Bernstein, I.B., Frieman, E.A., Kruskal, M.D. & Kulsrud, R.M. 1958 An energy principle for hydromagnetic stability problems. Proc. R. Soc. Lond. A 244, 17–40.Google Scholar
Blumen, W. 1975 Stability of non-planar shear flow of a stratified fluid. J. Fluid Mech. 68 (1), 177–189.CrossRefGoogle Scholar
Bogdan, T.J. & Cally, P.S. 1997 Waves in magnetized polytropes. Proc. R. Soc. Lond. A 453, 943–961.CrossRefGoogle Scholar
Cally, P.S. 1983 Complex eigenvalue bounds in magnetoatmospheric shear flow. I. Geophys. Astrophys. Fluid Dyn. 31, 43–55.CrossRefGoogle Scholar
Cally, P.S. 2000 A sufficient condition for instability in a sheared incompressible magnetofluid. Solar Phys. 194, 189–196.CrossRefGoogle Scholar
Candelier, J., Le Dizes, S. & Milet, C. 2011 Shear instability in a stratified fluid when shear and stratification are not aligned. J. Fluid Mech. 685, 191–201.CrossRefGoogle Scholar
Charbonneau, P, Tomczyk, S., Schou, J. & Thompson, M.J. 1998 The rotation of the solar core inferred by genetic forward modeling. Astrophys. J. 496, 1015–1030.CrossRefGoogle Scholar
Chen, J., Bai, J. & Le Dizes, S. 2016 Instability of a boundary layer flow on a vertical wall in a stably stratified fluid. J. Fluid Mech. 795, 262–277.CrossRefGoogle Scholar
Chimonas, G. 1970 The extension of the Miles-Howard theorem to compressible fluids. J. Fluid Mech. 43 (4), 833–836.CrossRefGoogle Scholar
Dandapat, B.S. & Gupta, A.S. 1977 Stability of magnetogasdynamic shear flow. Acta Mech. 28, 77–83.CrossRefGoogle Scholar
Deguchi, K. 2019 a High-speed shear driven dynamos. Part 1. Asymptotic analysis. J. Fluid Mech. 868, 176–211.CrossRefGoogle Scholar
Deguchi, K. 2019 b High-speed shear driven dynamos. Part 2. Numerical analysis. J. Fluid Mech. 876, 830–858.CrossRefGoogle Scholar
Deguchi, K. 2019 c Inviscid instability of a unidirectional flow sheared in two transverse directions. J. Fluid Mech. 874, 979–994.CrossRefGoogle Scholar
Deguchi, K. 2020 Subcritical magnetohydrodynamic instabilities: Chandrasekhar's theorem revisited. J. Fluid Mech. 882, A20.CrossRefGoogle Scholar
Deguchi, K. & Hall, P. 2014 The high Reynolds number asymptotic development of nonlinear equilibrium states in plane Couette flow. J. Fluid Mech. 750, 99–112.CrossRefGoogle Scholar
Dong, S., Krasnov, D. & Boeck, T. 2012 Secondary energy growth and turbulence suppression in conducting channel flow with streamwise magnetic field. Phys. Fluids 24, 074101.CrossRefGoogle Scholar
Dowling, T.E. 1995 Dynamics of Jovian atmospheres. Annu. Rev. Fluid Mech. 27, 293–334.CrossRefGoogle Scholar
Eckart, C. 1963 Extension of Howard's circle theorem to adiabatic jets. Phys. Fluids 6, 1042–1047.CrossRefGoogle Scholar
Facchini, G., Favier, B., Le Gal, P., Wang, M. & Le Bars, M. 2018 The linear instability of the stratified plane Couette flow. J. Fluid Mech. 25, 205–234.CrossRefGoogle Scholar
Frieman, E. & Rotenberg, M. 1960 On hydromagnetic stability of stationary equilibria. Rev. Mod. Phys. 32, 898–902.CrossRefGoogle Scholar
Fung, Y.T. 1986 On inviscid stratified parallel flows varying in two directions. Geophys. Astrophys. Fluid Dyn. 35, 57–70.CrossRefGoogle Scholar
Goldstein, M.E. 1976 Aeroacoustics. McGraw-Hill.Google Scholar
Gupta, A.S. 1992 Hydromagnetic stability of a stratified parallel flow varying in two directions. Astrophys. Space Sci. 198, 95–100.CrossRefGoogle Scholar
Hall, P. & Horseman, N. 1991 The linear inviscid secondary instability of longitudinal vortex structures in boundary layers. J. Fluid Mech. 232, 357–375.CrossRefGoogle Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.CrossRefGoogle Scholar
Hall, P. & Smith, F.T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.CrossRefGoogle Scholar
Hamilton, J.M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 25, 317–348.CrossRefGoogle Scholar
Henningson, D.S. 1987 Stability of parallel inviscid shear flow with mean spanwise variation. Tech. Rep. FFA-TN 1987–57. Aeronautical Research Institute of Sweden, Bromma.Google Scholar
Hocking, L.M. 1964 The instability of a non-uniform vortex sheet. J. Fluid Mech. 18, 177–186.CrossRefGoogle Scholar
Hocking, L.M. 1968 Long wavelength disturbances to non-planar parallel flow. J. Fluid Mech. 31 (4), 625–634.CrossRefGoogle Scholar
Howard, L.N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 13, 158–160.CrossRefGoogle Scholar
Howard, L.N. & Gupta, A.S. 1962 On the hydrodynamic and hydromagnetic stability of swirling flows. J. Fluid Mech. 14 (3), 463–476.CrossRefGoogle Scholar
Hughes, D.W. & Cattaneo, F. 1987 A new look at the instability of a stratified horizontal magnetic field. Geophys. Astrophys. Fluid Dyn. 39, 65–81.CrossRefGoogle Scholar
Hughes, D.W. & Tobias, S.M. 2001 On the instability of magnetohydrodynamic shear flows. Proc. R. Soc. Lond. A 457, 1365–1384.CrossRefGoogle Scholar
Hunt, J.C.R. 1966 On the stability of parallel flows with parallel magnetic fields. Proc. R. Soc. Lond. A 293, 342–358.Google Scholar
Jimenez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Kochar, G.T. & Jain, R.K. 1979 Note on Howard's semicircle theorem. J. Fluid Mech. 91 (3), 489–491.CrossRefGoogle Scholar
Li, Y. 2011 Stability criteria of 3D inviscid shears. Q. Appl. Maths 69, 379–387.CrossRefGoogle Scholar
Li, F. & Malik, M.R. 1995 Fundamental and subharmonic secondary instabilities of Görtler vortices. J. Fluid Mech. 297, 77–100.CrossRefGoogle Scholar
Lin, C.C. 1955 The Theory of Hydrodynamic Stability. Cambridge University Press.Google Scholar
Lucas, D., Caulfield, C.P. & Kerswell, R.R. 2017 Layer formation in horizontally forced stratified turbulence: connecting exact coherent structures to linear instabilities. J. Fluid Mech. 832, 409–437.CrossRefGoogle Scholar
McKeon, B.J. & Sharma, A.S. 2010 A critical layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Miles, J.W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10 (4), 496–508.CrossRefGoogle Scholar
Newcomb, W.A. 1961 Convective instability induced by gravity in a plasma with a frozen-in magnetic field. Phys. Fluids 4, 391–396.CrossRefGoogle Scholar
Ogilvie, G.I. & Proctor, M.R.E. 2003 On the relation between viscoelastic and magnetohydrodynamic flows and their instabilities. J. Fluid Mech. 476, 389–409.CrossRefGoogle Scholar
Parker, E.N. 1966 The dynamical state of the interstellar gas and field. Astrophys. J. 145, 811–833.CrossRefGoogle Scholar
Priede, J., Aleksandrova, S. & Molokov, S. 2010 Linear stability of Hunt's flow. J. Fluid Mech. 649, 115–134.CrossRefGoogle Scholar
Qi, T., Liu, C., Ni, M. & Yang, J. 2017 The linear stability of Hunt-Rayleigh–Bénard flow. Phys. Fluids 29, 064103.CrossRefGoogle ScholarPubMed
Rayleigh, Lord 1880 On the stability, or instability, of certain fluid motions. Proc. Lond. Math. Soc. 11, 57–70.Google Scholar
Riols, A., Rincon, F., Cossu, C., Lesur, G., Longaretti, P.-Y., Ogilvie, G.I. & Herault, J. 2013 Global bifurcations to subcritical magnetorotational dynamo action in Keplerian shear flow. J. Fluid Mech. 731, 1–45.CrossRefGoogle Scholar
Sasaki, E., Takehiro, S. & Yamada, M. 2012 A note on the stability of inviscid zonal jet flows on a rotating sphere. J. Fluid Mech. 710, 154–165.CrossRefGoogle Scholar
Thomas, V.L., Lieu, B.K., Jovanovic, M.R., Farrell, B.F., Ioannou, P.J. & Gayme, D.F. 2014 Self-sustaining turbulence in a restricted nonlinear model of plane Couette flow. Phys. Fluids 26, 105112.CrossRefGoogle Scholar
Thuburn, J. & Haynes, P. 1996 Bounds on the growth rate and phase velocity of instabilities in non-divergent barotropic flow on a sphere: a semicircle theorem. Q. J. R. Meteorol. Soc. 122, 779–787.CrossRefGoogle Scholar
Tobias, S.M. & Hughes, D.W. 2004 The influence of velocity shear on magnetic buoyancy instability in the solar tachocline. Astrophys. J. 603, 785–802.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.CrossRefGoogle Scholar
Waleffe, F. 2019 Semicircle theorem for streak instability. Fluid Dyn. Res. 51, 011403.CrossRefGoogle Scholar
Wang, J., Gibson, J.F. & Waleffe, F. 2007 Lower branch coherent states: transition and control. Phys. Rev. Lett. 98, 204501.CrossRefGoogle ScholarPubMed
Warren, F.W.G. 1970 A method for finding bounds for complex eigenvalues of second order systems. J. Inst. Maths Applics 6, 21–26.CrossRefGoogle Scholar
Yu, X. & Liu, J.T.C. 1991 The secondary instability in Goertler flow. Phys. Fluids 3, 1845–1847.CrossRefGoogle Scholar
Supplementary material: File

Deguchi supplementary material

Deguchi supplementary material

Download Deguchi supplementary material(File)
File 272.4 KB