Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-20T06:32:25.999Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of inertia on the time period of rotation of an anisotropic particle in simple shear flow

Published online by Cambridge University Press:  29 September 2017

Navaneeth K. Marath  and
Ganesh Subramanian Open the ORCID record for Ganesh Subramanian [Opens in a new window]
Navaneeth K. Marath
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore, 560 064, India
Ganesh Subramanian*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore, 560 064, India
*
†Email address for correspondence: sganesh@jncasr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

We calculate the leading-order correction to the time period of rotation of a neutrally buoyant spheroid of arbitrary aspect ratio, in a simple shear flow (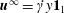$\boldsymbol{u}^{\infty }=\dot{\unicode[STIX]{x1D6FE}}y\mathbf{1}_{1}$; 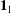$\mathbf{1}_{1}$ is the unit vector in the flow direction, $y$ being the coordinate along the gradient direction), in its long-time orbit set up by the weak fluid inertial drift at 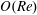$O(Re)$. Here, 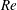$Re$ is the microscale Reynolds number, a dimensionless measure of the fluid inertial effects on the length scale of the spheroid, and is defined as 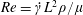$Re=\dot{\unicode[STIX]{x1D6FE}}L^{2}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D707}$, where 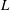$L$ is the semimajor axis of the spheroid, 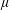$\unicode[STIX]{x1D707}$ and 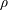$\unicode[STIX]{x1D70C}$ are respectively the viscosity and density of the fluid, and 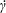$\dot{\unicode[STIX]{x1D6FE}}$ is the shear rate. This long-time orbit is the tumbling orbit for prolate spheroids; for oblate spheroids, it is the spinning orbit for aspect ratios greater than 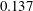$0.137$, and can be either the tumbling or the spinning orbit for oblate spheroids of aspect ratios less than 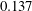$0.137$. We also calculate the leading-order correction to the time period of rotation of a neutrally buoyant triaxial ellipsoid in a simple shear flow, rotating with its intermediate principal axis aligned along the vorticity of the flow; the latter calculation is in light of recent evidence, by way of numerical simulations (Rosen, PhD dissertation, 2016, Stockholm), of the aforementioned rotation being stabilized by weak inertia. The correction to the time period for arbitrary 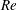$Re$ is expressed as a volume integral using a generalized reciprocal theorem formulation. For 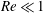$Re\ll 1$, it is shown that the correction at 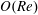$O(Re)$ is zero for spheroids (with aspect ratios of order unity) as well as triaxial ellipsoids in their long-time orbits. The first correction to the time period therefore occurs at 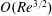$O(Re^{3/2})$, and has a singular origin, arising from fluid inertial effects in the outer region (distances from the spheroid or triaxial ellipsoid of the order of the inertial screening length of 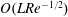$O(LRe^{-1/2})$), where the leading-order Stokes approximation ceases to be valid. Since the correction comes from the effects of inertia in the far field, the rotating spheroid (triaxial ellipsoid) is approximated as a time-dependent point-force-dipole singularity, allowing for the reciprocal theorem integral to be evaluated in Fourier space. It is shown for all relevant cases that fluid inertia at 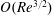$O(Re^{3/2})$ leads to an increase in the time period of rotation compared with that in the Stokes limit, consistent with the results of recent numerical simulations at finite 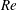$Re$. Finally, combination of the 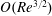$O(Re^{3/2})$ correction derived here with the 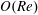$O(Re)$ correction derived earlier by Dabade et al. (J. Fluid Mech., vol. 791, 2016, 631703) yields a uniformly valid description of the first effects of inertia for spheroids of all aspect ratios, including prediction of the arrest of rotation for extreme-aspect-ratio spheroids.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 830 , 10 November 2017 , pp. 165 - 210
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arfken, G. B., Weber, H. J. & Harris, F. E. 2011 Mathematical Methods for Physicists: A Comprehensive Guide. Academic.Google Scholar
Childress, S. 1964 The slow motion of a sphere in a rotating, viscous fluid. J. Fluid Mech. 20 (02), 305–314.Google Scholar
Dabade, V., Marath, N. K. & Subramanian, G. 2016 The effect of inertia on the orientation dynamics of anisotropic particles in simple shear flow. J. Fluid Mech. 791, 631703.Google Scholar
De Gennes, P. G. 1974 Coil–stretch transition of dilute flexible polymers under ultrahigh velocity gradients. J. Chem. Phys. 60 (12), 5030–5042.CrossRefGoogle Scholar
Einarsson, J., Candelier, F., Lundell, F., Angilella, J. & Mehlig, B. 2015 Rotation of a spheroid in a simple shear at small Reynolds number. Phys. Fluids 27 (6), 063301.Google Scholar
Hinch, E. J. 1974 Mechanical models of dilute polymer solutions for strong flows with large polymer deformations. Proc. Coll. Int. CNRS Polym. Lubrification 233, 241–247.Google Scholar
Hinch, E. J. 1991 Perturbation Methods. Cambridge University Press.Google Scholar
Hinch, E. J. & Leal, L. G. 1979 Rotation of small non-axisymmetric particles in a simple shear flow. J. Fluid Mech. 92 (03), 591–607.CrossRefGoogle Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Kim, S. & Karrila, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann.Google Scholar
Leal, L. G. 1979 The motion of small particles in non-Newtonian fluids. J. Non-Newtonian Fluid Mech. 5, 33–78.Google Scholar
Leal, L. G. & Hinch, E. J. 1971 The effect of weak Brownian rotations on particles in shear flow. J. Fluid Mech. 46, 685–703.Google Scholar
Lin, C.-J., Peery, J. H. & Schowalter, W. R. 1970 Simple shear flow round a rigid sphere: inertial effects and suspension rheology. J. Fluid Mech. 44 (01), 1–17.Google Scholar
Mao, W. & Alexeev, A. 2014 Motion of spheroid particles in shear flow with inertia. J. Fluid Mech. 749, 145–166.CrossRefGoogle Scholar
Marath, N. K., Dwivedi, R. & Subramanian, G. 2017 An orientational order transition in a sheared suspension of anisotropic particles. J. Fluid Mech. (Rapids) 811, R3.CrossRefGoogle Scholar
Marath, N. K. & Subramanian, G. 2017 The orientation dynamics of anisotropic particles in a planar linear flow. J. Fluid Mech. (submitted).Google Scholar
Meibohm, J., Candelier, F., Rosén, T., Einarsson, J., Lundell, F. & Mehlig, B. 2016 Angular velocity of a spheroid log rolling in a simple shear at small Reynolds number. Phys. Rev. Fluids 1, 084203.Google Scholar
Mikulencak, D. R. & Morris, J. F. 2004 Stationary shear flow around fixed and free bodies at finite Reynolds number. J. Fluid Mech. 520, 215–242.CrossRefGoogle Scholar
Robertson, C. R. & Acrivos, A. 1970 Low Reynolds number shear flow past a rotating circular cylinder. Part 1. Momentum transfer. J. Fluid Mech. 40 (04), 685–703.Google Scholar
Rosen, T.2016 Angular dynamics of non-spherical particles in linear flows related to production of biobased materials. PhD dissertation. Stockholm.Google Scholar
Saffman, P. G. T 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22 (02), 385–400.Google Scholar
Stone, H., Brady, J. & Lovalenti, P. M.2000 Inertial effects on the rheology of suspensions and on the motion of individual particles (unpublished).Google Scholar
Subramanian, G. & Koch, D. L. 2005 Inertial effects on fibre motion in simple shear flow. J. Fluid Mech. 535, 383–414.Google Scholar
Subramanian, G. & Koch, D. L. 2006a Inertial effects on the orientation of nearly spherical particles in simple shear flow. J. Fluid Mech. 557, 257–296.Google Scholar
Subramanian, G. & Koch, D. L. 2006b Inertial effects on the transfer of heat or mass from neutrally buoyant spheres in a steady linear velocity field. Phys. Fluids 18 (7), 073302.Google Scholar
Subramanian, G., Koch, D. L., Zhang, J. & Yang, C. 2011 The influence of the inertially dominated outer region on the rheology of a dilute dispersion of low-Reynolds-number drops or rigid particles. J. Fluid Mech. 674, 307–358.CrossRefGoogle Scholar
Yarin, A. L., Gottlieb, O. & Roisman, I. V. 1997 Chaotic rotation of triaxial ellipsoids in simple shear flow. J. Fluid Mech. 340, 83–100.Google Scholar