Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-27T02:09:49.472Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of a sphere in inertial shear flow between parallel walls

Published online by Cambridge University Press:  29 March 2021

Andrew J. Fox ,
James W. Schneider  and
Aditya S. Khair Open the ORCID record for Aditya S. Khair [Opens in a new window]
Andrew J. Fox
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA15213, USA
James W. Schneider
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA15213, USA
Aditya S. Khair*
Affiliation:
Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA15213, USA
*
†Email address for correspondence: akhair@andrew.cmu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

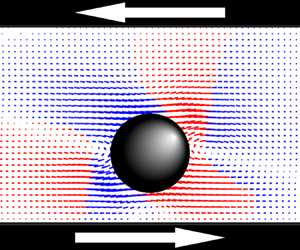
The motion of a rigid sphere in ambient simple shear flow of a Newtonian fluid between infinite parallel walls is calculated via the lattice Boltzmann method for various particle Reynolds numbers, ${\textit {Re}}_p=Ga^2/\nu$, where $G$ is the velocity gradient of the shear; $a$ is the particle radius; and $\nu$ is the kinematic viscosity of the fluid. For a neutrally buoyant sphere, there exists a critical ${\textit {Re}}_p$ below which the hydrodynamic lift force has a single zero crossing, driving the particle to an equilibrium position at the centre of the channel. Above the critical ${\textit {Re}}_p$, the equilibrium position of the sphere undergoes a supercritical pitchfork bifurcation; inertial lift creates three equilibrium positions: an unstable equilibrium position at the centre and two stable equilibria equidistant from the centre. The critical ${\textit {Re}}_p$ occurs below the transition to unsteady flow, and increases with increasing particle confinement ratio, $\kappa =a/H$, where $H$ is the channel height. The equilibrium position of a non-neutrally buoyant sphere shifts toward a confining wall of the channel, in a manner that is dependent on the orientation, i.e. horizontal or vertical, of the channel. In both channel alignments, the gravitational force breaks the symmetry of the particle dynamics about the centreline of the channel, resulting in an imperfect bifurcation above a critical ${\textit {Re}}_p$. However, a sufficiently strong gravitational force will break the bifurcation and produce a single off-centre equilibrium position. We finally consider a neutrally buoyant sphere under the cessation or reversal of shear flow.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Nonlinear Dynamical Systems: Bifurcation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A119
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aidun, C.K., Lu, Y. & Ding, E.-J. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.CrossRefGoogle Scholar
Asmolov, E.S. 1999 The inertial lift on a spherical particle in a plane poiseuille flow at large channel Reynolds number. J. Fluid Mech. 381, 63–87.CrossRefGoogle Scholar
Batchelor, G.K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.CrossRefGoogle Scholar
Chen, H., Chen, S. & Mathhaeus, W.H. 1992 Recovery of the Navier–Stokes equations using a lattice-gas Boltzmann method. Phys. Rev. A 45, R5339(R).CrossRefGoogle ScholarPubMed
Cox, R.G. & Brenner, H. 1968 The lateral migration of solid particles in poiseuille flow – I. Theory. Chem. Engng Sci. 23, 147–173.CrossRefGoogle Scholar
Drew, D.A. 1988 The lift force on a small sphere in the presence of a wall. Chem. Engng Sci. 43, 769–773.CrossRefGoogle Scholar
Ekanayake, N.I.K., Berry, J.D., Stickland, A.D., Dunstan, D.E., Muir, I.L., Dower, S.K. & Harvie, D.J.E. 2020 Lift and drag forces acting on a particle moving with zero slip in a linear shear flow near a wall. J. Fluid Mech. 904, A6.CrossRefGoogle Scholar
Feng, J., Hu, H.H. & Joseph, D.D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 2. Couette and Poiseuille flows. J. Fluid Mech. 277, 271–301.CrossRefGoogle Scholar
Fox, A.J., Schneider, J.W. & Khair, A.S. 2020 Inertial bifurcation of the equilibrium position of a neutrally-buoyant circular cylinder in shear flow between parallel walls. Phys. Rev. Res. 2, 013009.CrossRefGoogle Scholar
Gou, Y., Jia, Y., Wang, P. & Sun, C. 2018 Progress of inertial microfluidics in principle and application. Sensors 18, 1762.CrossRefGoogle ScholarPubMed
Halow, J.S. & Willis, G.B. 1970 a Experimental observations of sphere migration in Couette systems. Ind. Engng Chem. Fundam. 9, 603–607.CrossRefGoogle Scholar
Halow, J.S. & Willis, G.B. 1970 b Radial migration of spherical particles in Couette systems. AIChE J. 16, 281–286.CrossRefGoogle Scholar
Ho, B.P. & Leal, L.G. 1974 Inertial migration of rigid spheres in two-dimensional unidirectional flows. J. Fluid Mech. 65, 365–400.CrossRefGoogle Scholar
Huo, S., Zou, Q., Chen, S., Doolen, G. & Cogley, A.C. 1995 Simulation of cavity flow by lattice Boltzmann method. J. Comput. Phys. 118, 329–347.Google Scholar
Hur, S.C., Mach, A.J. & Di Carlo, D. 2011 High-throughput size-based rare cell enrichment using microscale vortices. Biomicrofluids 5, 022206.CrossRefGoogle ScholarPubMed
Jeffery, G.B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Ladd, A.J.C. 1994 a Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 271, 285–309.CrossRefGoogle Scholar
Ladd, A.J.C. 1994 b Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 271, 311–339.CrossRefGoogle Scholar
Li, M., Munoz, H.E., Goda, K. & Di Carlo, D. 2017 Shape-based separation of microalga euglena gracilis using inertial microfluidics. Sci. Rep. 7, 10802.CrossRefGoogle Scholar
Mach, A.J. & Di Carlo, D. 2010 Continuous scalable blood filtration device using inertial microfluidics. Biotechnol. Bioengng 107, 302–311.CrossRefGoogle ScholarPubMed
Mao, W. & Alexeev, A. 2014 Motion of spheroid particles in shear flow with inertia. J. Fluid Mech. 749, 145–166.CrossRefGoogle Scholar
Martel, J.M. & Toner, M. 2014 Inertial focusing in microfluidics. Annu. Rev. Biomed. Engng 16, 371–96.CrossRefGoogle Scholar
McLaughlin, J.B. 1991 Inertial migration of a small sphere in linear shear flows. J. Fluid Mech. 224, 261–274.CrossRefGoogle Scholar
McLaughlin, J.B. 1993 The lift on a small sphere in wall-bounded linear shear flows. J. Fluid Mech. 246, 249–265.CrossRefGoogle Scholar
McNamara, G.R. & Zanetti, G. 1988 Use of the Boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 61, 2332.CrossRefGoogle ScholarPubMed
Mikulencak, D.R. & Morris, J.F. 2004 Stationary shear flow around fixed and free bodies at finite Reynolds number. J. Fluid Mech. 520, 215–242.CrossRefGoogle Scholar
Miura, H. & Kimoto, M. 2005 A comparison of grid quality of optimized spherical hexagonal–pentagonal geodesic grids. Mon. Weath. Rev. 133, 2817–2833.CrossRefGoogle Scholar
Nirschl, H., Dwyer, H.A. & Denk, V. 1995 Three-dimensional calculations of the simple shear flow around a single particle between two moving walls. J. Fluid Mech. 283, 273–285.CrossRefGoogle Scholar
Nivedita, N. & Papautsky, I. 2013 Continuous separation of blood cells in spiral microfluidic devices. Biomicrofluidics 7, 054101.CrossRefGoogle ScholarPubMed
Poe, G.G. & Acrivos, A. 1975 Closed streamline flows past rotating single spheres and cylinders: inertia effects. J. Fluid Mech. 72, 605–623.CrossRefGoogle Scholar
Rosen, T., Do-Quang, M., Aidun, C.K. & Lundell, F. 2015 a The dynamical states of a prolate spheroidal particle suspended in shear flow as a consequence of particle and fluid inertia. J. Fluid Mech. 771, 115–158.CrossRefGoogle Scholar
Rosen, T., Einarsson, J., Nordmark, A., Aidun, C.K., Lundell, F. & Mehlig, B. 2015 b Numerical analysis of the angular motion of a neutrally buoyant spheroid in shear flow at small Reynolds numbers. Phys. Rev. E 92, 063022.CrossRefGoogle ScholarPubMed
Rosen, T., Lundell, F. & Aidun, C.K. 2014 Effect of fluid inertia on the dynamics and scaling of neutrally buoyant particles in shear flow. J. Fluid Mech. 738, 563–590.CrossRefGoogle Scholar
Rubinow, S.I. & Keller, J.B. 1961 The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 11, 447–459.CrossRefGoogle Scholar
Rust, A.C. & Manga, M. 2002 Bubble shapes and orientations in low Re simple shear flow. J. Colloid Interface Sci. 249, 479–480.CrossRefGoogle Scholar
Saffman, P.G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22, 385–400.CrossRefGoogle Scholar
Schonberg, J.A. & Hinch, E.J. 1989 Inertial migration of a sphere in Poiseuille flow. J. Fluid Mech. 203, 517–524.CrossRefGoogle Scholar
Segre, G. & Silberberg, A. 1961 Radial particle displacements in Poiseuille flow of suspensions. Nature 189, 209–210.CrossRefGoogle Scholar
Segre, G. & Silberberg, A. 1962 Behavior of macroscopic rigid spheres in Poiseuille flow. J. Fluid Mech. 14, 136–157.CrossRefGoogle Scholar
Taylor, G.I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. A 146, 501–523.Google Scholar
Wu, J. & Aidun, C.K. 2010 Simulating 3d deformable particle suspensions using lattice Boltzmann method with discrete external boundary force. Intl J. Numer. Meth. Fluids 62, 765–783.Google Scholar