Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-17T10:54:37.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Diagnosing diabatic effects on the available energy of stratified flows in inertial and non-inertial frames

Published online by Cambridge University Press:  27 December 2018

Alberto Scotti Open the ORCID record for Alberto Scotti [Opens in a new window]  and
Pierre-Yves Passaggia Open the ORCID record for Pierre-Yves Passaggia [Opens in a new window]
Alberto Scotti*
Affiliation:
Department of Marine Sciences, University of North Carolina, NC 27599, USA
Pierre-Yves Passaggia
Affiliation:
Department of Marine Sciences, University of North Carolina, NC 27599, USA
*
†Email address for correspondence: ascotti@unc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The concept of available energy in a stratified fluid is revisited from the point of view of non-canonical Hamiltonian systems. We show that the concept of available energy arises when we minimize the energy subject to the constraints associated with the existence of Lagrangian invariants. The non-canonical structure implies that there exists a class of dynamically equivalent Hamiltonians, related by a local (in phase space) gauge symmetry. A local diagnostic energy can be defined via the Hamiltonian density chosen imposing a specific gauge-fixing condition on the class of dynamically similar Hamiltonians. The gauge-fixing condition that we introduce selects a specific local diagnostic energy which is well suited to study the effect of diabatic processes on the evolution of the available energy. Non-inertial effects, which are notoriously elusive to capture within an energetic framework, are naturally included via conservation of potential vorticity. We apply the framework to stratified flows in inertial and non-inertial frames. For stratified Boussinesq flows, when the initial distribution of potential vorticity is even around the origin, our framework recovers the available potential energy introduced by Holliday & McIntyre (J. Fluid Mech., vol. 107, 1981, pp. 221–225), and as such, depends only on the mass distribution of the flow. In rotating flows, the isopycnals of the ground state are generally not flat, and the ground state may have kinetic energy. We finally demonstrate that flows in non-inertial frames characterized by a low Rossby number (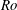$Ro$), the local diagnostic energy has, to lowest order in 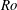$Ro$, a universal character.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Mathematical Foundations: Hamiltonian theory Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 608 - 642
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abarbanel, H. D., Holm, D. D., Marsden, J. E. & Ratiu, T. S. 1986 Nonlinear stability analysis of stratified fluid equilibria. Phil. Trans. R. Soc. Lond. A 318 (1543), 349–409.Google Scholar
Åkervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18 (6), 068102.Google Scholar
Andrews, D. G. 1981 A note on potential energy density in a stratified compressible fluid. J. Fluid Mech. 107, 227–236.Google Scholar
Arobone, E. & Sarkar, S. 2015 Effects of three-dimensionality on instability and turbulence in a frontal zone. J. Fluid Mech. 784, 252–273.Google Scholar
Besse, N. & Frisch, U. 2017 Geometric formulation of the Cauchy invariants for incompressible Euler flow in flat and curved spaces. J. Fluid Mech. 825, 412–478.Google Scholar
Callies, J., Ferrari, R., Klymak, J. M. & Gula, J. 2015 Seasonality in submesoscale turbulence. Nature Commun. 6, 6862.Google Scholar
Codoban, S. & Shepherd, T. G. 2003 Energetics of a symmetric circulation including momentum constraints. J. Atmos. Sci. 60 (16), 2019–2028.Google Scholar
Cunha, G., Passaggia, P.-Y. & Lazareff, M. 2015 Optimization of the selective frequency damping parameters using model reduction. Phys. Fluids 27 (9), 094103.Google Scholar
DAsaro, E., Lee, C., Rainville, L., Harcourt, R. & Thomas, L. 2011 Enhanced turbulence and energy dissipation at ocean fronts. Science 332 (6027), 318–322.Google Scholar
Deloncle, A., Chomaz, J.-M. & Billant, P. 2007 Three-dimensional stability of a horizontally sheared flow in a stably stratified fluid. J. Fluid Mech. 570, 297–305.Google Scholar
Flanders, H. 1989 Differential Forms with Applications to the Physical Sciences. Academic, Reprinted by Dover Publications, Minneola, NY.Google Scholar
Frankel, T. 2011 The Geometry of Physics: An Introduction. Cambridge University Press.Google Scholar
Gay-Balmaz, F. & Holm, D. D. 2013 Selective decay by Casimir dissipation in inviscid fluids. Nonlinearity 26 (2), 495–524.Google Scholar
Gilbert, A. D. & Vanneste, J. 2018 Geometric generalised Lagrangian-mean theories. J. Fluid Mech. 839, 95–134.Google Scholar
Haney, S., Fox-Kemper, B., Julien, K. & Webb, A. 2015 Symmetric and geostrophic instabilities in the wave-forced ocean mixed layer. J. Phys. Oceanogr. 45 (12), 3033–3056.Google Scholar
Holliday, D. & McIntyre, M. E. 1981 On potential energy density in an incompressible stratified fluid. J. Fluid Mech. 107, 221–225.Google Scholar
Holm, D. D. 2008 Geometric Mechanics. Part I: Dynamics and Symmetry. Imperial College Press.Google Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40, 169–184.Google Scholar
Kucharski, F. & Thorpe, A. J. 2000 Local energetics of an idealized baroclinic wave using extended exergy. J. Atmos. Sci. 57 (19), 3272–3284.Google Scholar
Lamb, K. 2008 On the calculation of the available potential energy of an isolated perturbation in a density stratified fluid. J. Fluid Mech. 597, 415–427.Google Scholar
Lévy, M., Ferrari, R., Franks, P. J. S., Martin, A. P. & Rivière, P. 2012 Bringing physics to life at the submesoscale. Geophys. Res. Lett. 39 (14).Google Scholar
Littlejohn, R. G. 1982 Singular Poisson tensors. Math. Meth. Hydrodyn. Integr. Dynam. Syst. 88, 47–66.Google Scholar
Lorenz, E. N. 1955 Available potential energy and the maintenance of the general circulation. Tellus 7, 157–167.Google Scholar
MacCready, P. & Giddings, S. N. 2016 The mechanical energy budget of a regional ocean model. J. Phys. Oceanogr. 46 (9), 2719–2733.Google Scholar
Mahadevan, A. 2016 The impact of submesoscale physics on primary productivity of plankton. Annu. Rev. Marine Sci. 8, 161–184.Google Scholar
Margules, M. 1903 Über die Energie der Stürme. Jahrb. k. k. Zent.-Anst. für Meteorol. und Erdmagnet. 48, 1–26.Google Scholar
Marino, R., Pouquet, A. & Rosenberg, D. 2015 Resolving the paradox of oceanic large-scale balance and small-scale mixing. Phys. Rev. Lett. 114 (11), 114504.Google Scholar
McWilliams, J. C. 2016 Submesoscale currents in the ocean. Proc. R. Soc. Lond. A 472, 20160117.Google Scholar
Methven, J. & Berrisford, P. 2015 The slowly evolving background state of the atmosphere. Q. J. R. Meteor. Soc. 141 (691), 2237–2258.Google Scholar
Nikurashin, M., Vallis, G. K. & Adcroft, A. 2013 Routes to energy dissipation for geostrophic flows in the southern ocean. Nature Geo. 6 (1), 48–51.Google Scholar
Passaggia, P.-Y., Scotti, A. & White, B. 2017 Transition and turbulence in horizontal convection. Linear stability analysis. J. Fluid Mech 821, 31–57.Google Scholar
Pedlosky, J. 1986 Geophysical Fluid Dynamics. Springer.Google Scholar
Renaud, A., Venaille, A. & Bouchet, F. 2016 Equilibrium statistical mechanics and energy partition for the shallow water model. J. Stat. Phys. 163 (4), 784–843.Google Scholar
Salmon, R. 1988 Hamiltonian fluid mechanics. Annu. Rev. Fluid Mech. 20 (1), 225–256.Google Scholar
Scotti, A. 2015 Biases in Thorpe-scale estimates of turbulence dissipation. Part II. Energetics arguments and turbulence simulations. J. Phys. Oceanogr. 45 (10), 2522–2543.Google Scholar
Scotti, A., Beardsley, R. & Butman, B. 2006 On the interpretation of energy and energy fluxes of nonlinear internal waves: an example from Massachusetts Bay. J. Fluid Mech. 561, 103–112.Google Scholar
Scotti, A. & White, B. 2014 Diagnosing mixing in stratified turbulent flows with a locally defined available potential energy. J. Fluid Mech. 740, 114–135.Google Scholar
Shepherd, T. G. 1990 A general method for finding extremal states of Hamiltonian dynamical systems, with applications to perfect fluids. J. Fluid Mech. 213, 573–587.Google Scholar
Shepherd, T. G. 1993 A unified theory of available potential-energy. Atmos.-Ocean 31, 1–26.Google Scholar
Simpson, J. J. & Lynn, R. J. 1990 A mesoscale eddy dipole in the offshore California Current. J. Geophys. Res. Oceans 95 (C8), 13009–13022.Google Scholar
Sternberg, S. 2012 Curvature in Mathematics and Physics. Dover.Google Scholar
von Storch, J.-S., Eden, C., Fast, I., Haak, H., Hernàndez-Deckers, D., Maier-Reimer, E., Marotzke, J. & Stammer, D. 2012 An estimate of the Lorenz Energy Cycle for the World Ocean based on the 1/100 STORM/NCEP Simulation. J. Phys. Oceanogr. 42, 2185–2205.Google Scholar
Tailleux, R. 2018 Local available energetics of multicomponent compressible stratified fluids. J. Fluid Mech. 842.Google Scholar
Taylor, J. R. & Ferrari, R. 2010 Buoyancy and wind-driven convection at mixed layer density fronts. J. Phys. Oceanogr. 40 (6), 1222–1242.Google Scholar
Thomas, L. N. 2005 Destruction of potential vorticity by winds. J. Phys. Oceanogr. 35 (12), 2457–2466.Google Scholar
Thomas, L. N. 2017 On the modifications of near-inertial waves at fronts: implications for energy transfer across scales. Ocean Dyn. 67 (10), 1335–1350.Google Scholar
Vallis, G. K., Carnevale, G. F. & Young, W. R. 1989 Extremal energy properties and construction of stable solutions of the Euler equations. J. Fluid Mech. 207, 133–152.Google Scholar
Venaille, A., Gostiaux, L. & Sommeria, J. 2017 A statistical mechanics approach to mixing in stratified fluids. J. Fluid Mech. 810, 554–583.Google Scholar
Winters, K. B. & Barkan, R. 2012 Available potential energy density for Boussinesq fluid flow. J. Fluid Mech. 714, 476–488.Google Scholar
Winters, K. B. & D’Asaro, E. A. 1996 Diascalar flux and the rate of fluid mixing. J. Fluid Mech. 317, 179–193.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Zemskova, V. E., White, B. L. & Scotti, A. 2015 Available potential energy and the general circulation: partitioning wind, buoyancy forcing, and diapycnal mixing. J. Phys. Oceanogr. 45 (6), 1510–1531.Google Scholar
Zhang, Z., Wang, W. & Qiu, B. 2014 Oceanic mass transport by mesoscale eddies. Science 345 (6194), 322–324.Google Scholar