Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-17T13:18:26.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Data-driven reduced modelling of turbulent Rayleigh–Bénard convection using DMD-enhanced fluctuation–dissipation theorem

Published online by Cambridge University Press:  06 August 2018

M. A. Khodkar  and
Pedram Hassanzadeh Open the ORCID record for Pedram Hassanzadeh [Opens in a new window]
M. A. Khodkar
Affiliation:
Department of Mechanical Engineering, Rice University, Houston, TX, USA
Pedram Hassanzadeh*
Affiliation:
Department of Mechanical Engineering, Rice University, Houston, TX, USA Department of Earth, Environmental, and Planetary Sciences, Rice University, Houston, TX, USA
*
†Email address for correspondence: pedram@rice.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A data-driven model-free framework is introduced for the calculation of reduced-order models (ROMs) capable of accurately predicting time-mean responses to external forcings, or forcings needed for specified responses, e.g. for control, in fully turbulent flows. The framework is based on using the fluctuation–dissipation theorem (FDT) in the space of a limited number of modes obtained from dynamic mode decomposition (DMD). Use of the DMD modes as the basis functions, rather than the commonly used proper orthogonal decomposition modes, resolves a previously identified problem in applying FDT to high-dimensional non-normal turbulent flows. 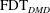Employing this DMD-enhanced FDT method ($\text{FDT}_{DMD}$), a linear ROM with horizontally averaged temperature as state vector is calculated for a 3D Rayleigh–Bénard convection system at a Rayleigh number of 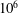$10^{6}$ using data obtained from direct numerical simulation. The calculated ROM performs well in various tests for this turbulent flow, suggesting 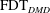$\text{FDT}_{DMD}$ as a promising method for developing ROMs for high-dimensional turbulent systems.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Turbulent Flows: Turbulent convection
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 852 , 10 October 2018 , R3
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arbabi, H. & Mezić, I. 2017 Ergodic theory, dynamic mode decomposition, and computation of spectral properties of the Koopman operator. SIAM J. Appl. Dyn. Syst. 16 (4), 2096–2126.Google Scholar
Brunton, S. L., Brunton, B. W., Proctor, J. L., Kaiser, E. & Kutz, J. N. 2017 Chaos as an intermittently forced linear system. Nat. Commun. 8 (1), 1–9.Google Scholar
Cooper, F. C., Esler, J. G. & Haynes, P. H. 2013 Estimation of the local response to a forcing in a high dimensional system using the fluctuation–dissipation theorem. Nonlinear Process. Geophys. 20 (2), 239–248.Google Scholar
Cooper, F. C. & Haynes, P. H. 2011 Climate sensitivity via a nonparametric fluctuation–dissipation theorem. J. Atmos. Sci. 68 (5), 937–953.Google Scholar
Fuchs, D., Sherwood, S. & Hernandez, D. 2015 An exploration of multivariate fluctuation dissipation operators and their response to sea surface temperature perturbations. J. Atmos. Sci. 72 (1), 472–486.Google Scholar
Giannakis, D. 2017 Data-driven spectral decomposition and forecasting of ergodic dynamical systems. Appl. Comput. Harmon. Anal. (in press).Google Scholar
Gritsun, A. & Branstator, G. 2007 Climate response using a three-dimensional operator based on the fluctuation–dissipation theorem. J. Atmos. Sci. 64 (7), 2558–2575.Google Scholar
Hassanzadeh, P. & Kuang, Z. 2016a The linear response function of an idealized atmosphere. Part I. Construction using Green’s functions and applications. J. Atmos. Sci. 73 (9), 3423–3439.Google Scholar
Hassanzadeh, P. & Kuang, Z. 2016b The linear response function of an idealized atmosphere. Part II. Implications for the practical use of the fluctuation–dissipation theorem and the role of operator’s non-normality. J. Atmos. Sci. 73 (9), 3441–3452.Google Scholar
Hassanzadeh, P., Kuang, Z. & Farrell, B. F. 2014 Responses of midlatitude blocks and wave amplitude to changes in the meridional temperature gradient in an idealized dry GCM. Geophys. Res. Lett. 41 (14), 5223–5232.Google Scholar
Khodkar, M. A., Hassanzadeh, P., Saleh, N. & Grover, P.2018 Reduced-order modeling of fully turbulent buoyancy-driven flows using the Green’s function method. arXiv:1805.01596.Google Scholar
Klus, S., Koltai, P. & Schütte, C. 2016 On the numerical approximation of the Perron–Frobenius and Koopman operator. J. Comput. Dyn. 3 (1), 51–79.Google Scholar
Koopman, B. O. 1931 Hamiltonian systems and transformation in Hilbert space. Proc. Natl Acad. Sci. USA 17 (5), 315–318.Google Scholar
Korda, M. & Mezić, I. 2018 On convergence of extended dynamic mode decomposition to the Koopman operator. J. Nonlinear Sci. 28 (2), 687–710.Google Scholar
Kramer, B., Grover, P., Boufounos, P., Nabi, S. & Benosman, M. 2017 Sparse sensing and DMD-based identification of flow regimes and bifurcations in complex flows. SIAM J. Appl. Dyn. Syst. 16 (2), 1164–1196.Google Scholar
Kuang, Z. 2010 Linear response functions of a cumulus ensemble to temperature and moisture perturbations and implications for the dynamics of convectively coupled waves. J. Atmos. Sci. 67 (4), 941–962.Google Scholar
Kubo, R. 1966 The fluctuation–dissipation theorem. Rep. Prog. Phys. 29 (1), 255–284.Google Scholar
Lasota, A. & Mackey, M. C. 2013 Chaos, Fractals, and Noise: Stochastic Aspects of Dynamics, vol. 97. Springer Science and Business Media.Google Scholar
Leith, C. E. 1975 Climate response and fluctuation dissipation. J. Atmos. Sci. 32 (10), 2022–2026.Google Scholar
Lutsko, N. J., Held, I. M. & Zurita-Gotor, P. 2015 Applying the fluctuation–dissipation theorem to a two-layer model of quasigeostrophic turbulence. J. Atmos. Sci. 72 (8), 3161–3177.Google Scholar
Majda, A., Abramov, R. V. & Grote, M. J. 2005 Information Theory and Stochastics for Multiscale Nonlinear Systems, vol. 25. American Mathematical Society.Google Scholar
Mezić, I. 2005 Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 41 (1–3), 309–325.Google Scholar
Mezić, I. 2013 Analysis of fluid flows via spectral properties of the Koopman operator. Annu. Rev. Fluid Mech. 45, 357–378.Google Scholar
Nyquist, H. 1928 Thermal agitation of electric charge in conductors. Phys. Rev. 32 (1), 110–113.Google Scholar
Penland, C. 1989 Random forcing and forecasting using principal oscillation pattern analysis. Mon. Weath. Rev. 117 (10), 2165–2185.Google Scholar
Ring, M. J. & Plumb, R. A. 2008 The response of a simplified GCM to axisymmetric forcings: applicability of fluctuation–dissipation theorem. J. Atmos. Sci. 65 (12), 3880–3898.Google Scholar
Rowley, C. W. & Dawson, S. T. M. 2017 Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 49, 387–417.Google Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Tu, J. H., Rowley, C. W., Luchtenburg, D. M., Brunton, S. L. & Kutz, J. N. 2014 On dynamic mode decomposition: theory and applications. J. Comput. Dyn. 1, 391–421.Google Scholar
Williams, M. O., Kevrekidis, I. G. & Rowley, C. W. 2015 A data-driven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. 25 (6), 1307–1346.Google Scholar