Hostname: page-component-848d4c4894-8kt4b Total loading time: 0 Render date: 2024-06-22T01:32:25.537Z Has data issue: false hasContentIssue false
  • English
  • Français

Bio-inspired variable-stiffness flaps for hybrid flow control, tuned via reinforcement learning

Published online by Cambridge University Press:  05 February 2023

Nirmal J. Nair Open the ORCID record for Nirmal J. Nair [Opens in a new window]  and
Andres Goza Open the ORCID record for Andres Goza [Opens in a new window]
Nirmal J. Nair*
Affiliation:
Department of Aerospace Engineering, University of Illinois Urbana-Champaign, Urbana, IL 61801, USA
Andres Goza
Affiliation:
Department of Aerospace Engineering, University of Illinois Urbana-Champaign, Urbana, IL 61801, USA
*
†Email address for correspondence: njn2@illinois.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

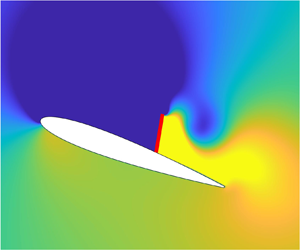
A bio-inspired, passively deployable flap attached to an airfoil by a torsional spring of fixed stiffness can provide significant lift improvements at post-stall angles of attack. In this work, we describe a hybrid active–passive variant to this purely passive flow control paradigm, where the stiffness of the hinge is actively varied in time to yield passive fluid–structure interaction of greater aerodynamic benefit than the fixed-stiffness case. This hybrid active–passive flow control strategy could potentially be implemented using variable-stiffness actuators with less expense compared with actively prescribing the flap motion. The hinge stiffness is varied via a reinforcement-learning-trained closed-loop feedback controller. A physics-based penalty and a long–short-term training strategy for enabling fast training of the hybrid controller are introduced. The hybrid controller is shown to provide lift improvements as high as 136 % and 85 % with respect to the flapless airfoil and the best fixed-stiffness case, respectively. These lift improvements are achieved due to large-amplitude flap oscillations as the stiffness varies over four orders of magnitude, whose interplay with the flow is analysed in detail.

JFM classification

Mathematical Foundations: Machine learning
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 956 , 10 February 2023 , R4
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahuja, S. & Rowley, C.W. 2010 Feedback control of unstable steady states of flow past a flat plate using reduced-order estimators. J. Fluid Mech. 645, 447–478.CrossRefGoogle Scholar
Arivoli, D & Singh, I. 2016 Self-adaptive flaps on low aspect ratio wings at low Reynolds numbers. Aerosp. Sci. Technol. 59, 78–93.Google Scholar
Baumeister, T., Brunton, S.L. & Kutz, J.N. 2018 Deep learning and model predictive control for self-tuning mode-locked lasers. J. Opt. Soc. Am. B 35 (3), 617–626.CrossRefGoogle Scholar
Bieker, K., Peitz, S., Brunton, S.L., Kutz, J.N. & Dellnitz, M. 2020 Deep model predictive flow control with limited sensor data and online learning. Theor. Comput. Fluid Dyn. 34, 1–15.Google Scholar
Bramesfeld, G. & Maughmer, M.D 2002 Experimental investigation of self-actuating, upper-surface, high-lift-enhancing effectors. J. Aircraft 39 (1), 120–124.CrossRefGoogle Scholar
Diller, S., Majidi, C. & Collins, S.H. 2016 A lightweight, low-power electroadhesive clutch and spring for exoskeleton actuation. In 2016 IEEE International Conference on Robotics and Automation (ICRA), pp. 682–689. IEEE.CrossRefGoogle Scholar
Duan, C. & Wissa, A. 2021 Covert-inspired flaps for lift enhancement and stall mitigation. Bioinspir. Biomim. 16, 046020.CrossRefGoogle ScholarPubMed
Fan, D., Yang, L., Wang, Z., Triantafyllou, M.S. & Karniadakis, G.E. 2020 Reinforcement learning for bluff body active flow control in experiments and simulations. Proc. Natl Acad. Sci. USA 117 (42), 26091–26098.CrossRefGoogle ScholarPubMed
Garnier, P., Viquerat, J., Rabault, J., Larcher, A., Kuhnle, A. & Hachem, E. 2021 A review on deep reinforcement learning for fluid mechanics. Comput. Fluids 225, 104973.CrossRefGoogle Scholar
Ham, R., Sugar, T., Vanderborght, B., Hollander, K. & Lefeber, D. 2009 Compliant actuator designs. IEEE J. Rob. Autom. Mag. 3 (16), 81–94.CrossRefGoogle Scholar
Kim, J. & Bewley, T.R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.CrossRefGoogle Scholar
Li, J. & Zhang, M. 2022 Reinforcement-learning-based control of confined cylinder wakes with stability analyses. J. Fluid Mech. 932, A44.CrossRefGoogle Scholar
Mohan, A.T. & Gaitonde, D.V. 2018 A deep learning based approach to reduced order modeling for turbulent flow control using LSTM neural networks. arXiv:1804.09269.Google Scholar
Nair, N.J. & Goza, A. 2022 a Fluid–structure interaction of a bio-inspired passively deployable flap for lift enhancement. Phys. Rev. Fluids 7, 064701.CrossRefGoogle Scholar
Nair, N.J. & Goza, A. 2022 b A strongly coupled immersed boundary method for fluid–structure interaction that mimics the efficiency of stationary body methods. J. Comput. Phys. 454, 110897.CrossRefGoogle Scholar
Nota, C. & Thomas, P.S. 2019 Is the policy gradient a gradient? arXiv:1906.07073.Google Scholar
Paris, R., Beneddine, S. & Dandois, J. 2021 Robust flow control and optimal sensor placement using deep reinforcement learning. J. Fluid Mech. 913, A25.CrossRefGoogle Scholar
Pawar, S. & Maulik, R. 2021 Distributed deep reinforcement learning for simulation control. Mach. Learn. Sci. Technol. 2 (2), 025029.CrossRefGoogle Scholar
Peitz, S., Otto, S.E. & Rowley, C.W. 2020 Data-driven model predictive control using interpolated koopman generators. SIAM J. Appl. Dyn. Syst. 19 (3), 2162–2193.CrossRefGoogle Scholar
Rabault, J., Kuchta, M., Jensen, A., Réglade, U. & Cerardi, N. 2019 Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J. Fluid Mech. 865, 281–302.CrossRefGoogle Scholar
Rabault, J. & Kuhnle, A. 2019 Accelerating deep reinforcement learning strategies of flow control through a multi-environment approach. Phys. Fluids 31 (9), 094105.CrossRefGoogle Scholar
Raffin, A., Hill, A., Gleave, A., Kanervisto, A., Ernestus, M. & Dormann, N. 2021 Stable-baselines3: reliable reinforcement learning implementations. J. Mach. Learn. Res. 22 (268), 1–8.Google Scholar
Rosti, M.E., Omidyeganeh, M. & Pinelli, A. 2018 Passive control of the flow around unsteady aerofoils using a self-activated deployable flap. J. Turbul. 19 (3), 204–228.CrossRefGoogle Scholar
Schulman, J., Wolski, F., Dhariwal, P., Radford, A. & Klimov, O. 2017 Proximal policy optimization algorithms. arXiv:1707.06347.Google Scholar
Sun, J., Guan, Q., Liu, Y. & Leng, J. 2016 Morphing aircraft based on smart materials and structures: a state-of-the-art review. J. Intell. Mater. Syst. Struct. 27 (17), 2289–2312.CrossRefGoogle Scholar
Sutton, R.S. & Barto, A.G. 2018 Reinforcement Learning: An Introduction. MIT Press.Google Scholar
Taira, K. & Colonius, T.I.M 2009 Three-dimensional flows around low-aspect-ratio flat-plate wings at low reynolds numbers. J. Fluid Mech. 623, 187–207.CrossRefGoogle Scholar
Verma, S., Novati, G. & Koumoutsakos, P. 2018 Efficient collective swimming by harnessing vortices through deep reinforcement learning. Proc. Natl Acad. Sci. USA 115 (23), 5849–5854.CrossRefGoogle ScholarPubMed
Viquerat, J., Rabault, J., Kuhnle, A., Ghraieb, H., Larcher, A. & Hachem, E. 2021 Direct shape optimization through deep reinforcement learning. J. Comput. Phys. 428, 110080.CrossRefGoogle Scholar
Wolf, S., et al. 2015 Variable stiffness actuators: review on design and components. IEEE/ASME Trans. Mech. 21 (5), 2418–2430.Google Scholar
Zhang, K., Hayostek, S., Amitay, M., He, W., Theofilis, V. & Taira, K. 2020 On the formation of three-dimensional separated flows over wings under tip effects. J. Fluid Mech. 895, A9.CrossRefGoogle Scholar
Zhu, Y., Tian, F.-B., Young, J., Liao, J.C. & Lai, J.C.S. 2021 A numerical study of fish adaption behaviors in complex environments with a deep reinforcement learning and immersed boundary–lattice boltzmann method. Sci. Rep. 11 (1), 1–20.Google ScholarPubMed