Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-26T21:57:58.768Z Has data issue: false hasContentIssue false
  • English
  • Français

Adaptive stochastic trajectory modelling in the chaotic advection regime

Published online by Cambridge University Press:  13 March 2015

J. G. Esler
J. G. Esler*
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK
*
†Email address for correspondence: gavin@math.ucl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by the goal of improving and augmenting stochastic Lagrangian models of particle dispersion in turbulent flows, techniques from the theory of stochastic processes are applied to a model transport problem. The aim is to find an efficient and accurate method to calculate the total tracer transport between a source and a receptor when the flow between the two locations is weak, rendering direct stochastic Lagrangian simulation prohibitively expensive. Importance sampling methods that combine information from stochastic forward and back trajectory calculations are proposed. The unifying feature of the new methods is that they are developed using the observation that a perfect strategy should distribute trajectories in proportion to the product of the forward and adjoint solutions of the transport problem, a quantity here termed the ‘density of trajectories’ 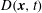$D(\boldsymbol{x},t)$. Two such methods are applied to a ‘hard’ model problem, in which the prescribed kinematic flow is in the large-Péclet-number chaotic advection regime, and the transport problem requires simulation of a complex distribution of well-separated trajectories. The first, Milstein’s measure transformation method, involves adding an artificial velocity to the trajectory equation and simultaneously correcting for the weighting given to each particle under the new flow. It is found that, although a ‘perfect’ artificial velocity 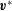$\boldsymbol{v}^{\ast }$ exists, which is shown to distribute the trajectories according to 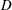$D$, small errors in numerical estimates of 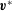$\boldsymbol{v}^{\ast }$ cumulatively lead to difficulties with the method. A second method is Grassberger’s ‘go-with-the-winners’ branching process, where trajectories found unlikely to contribute to the net transport (losers) are periodically removed, while those expected to contribute significantly (winners) are split. The main challenge of implementation, which is finding an algorithm to select the winners and losers, is solved by a choice that explicitly forces the distribution towards a numerical estimate of 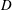$D$ generated from a previous back trajectory calculation. The result is a robust and easily implemented algorithm with typical variance up to three orders of magnitude lower than the direct approach.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Mathematical Foundations: Computational methods
Type
Papers
Information
Journal of Fluid Mechanics , Volume 769 , 25 April 2015 , pp. 1 - 25
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ades, M. & van Leeuwen, P. J. 2013 An exploration of the equivalent weights particle filter. Q. J. R. Meteorol. Soc. 139, 820–840.Google Scholar
Dagan, G. 1987 Theory of solute transport by groundwater. Annu. Rev. Fluid Mech. 19 (1), 183–213.Google Scholar
Devenish, B. J., Thomson, D. J., Marenco, F., Leadbetter, S. J., Ricketts, H. & Dacre, H. F. 2011 A study of the arrival over the United Kingdom in April 2010 of the Eyjafjallajokull ash cloud using ground-based lidar and numerical simulations. Atmos. Environ. 48, 152–164.Google Scholar
Esler, J. G. 2008 Robust and leaky transport barriers in unstable baroclinic flows. Phys. Fluids 20, 116602.Google Scholar
Forster, C., Stohl, A. & Seibert, P. 2007 Parameterization of convective transport in a Lagrangian particle dispersion model and its evaluation. J. Appl. Meteorol. 46, 403–422.Google Scholar
Gardiner, C. W. 2009 Stochastic Methods: A Handbook for the Natural and Social Sciences, 4th edn. Springer.Google Scholar
Grassberger, P. 1997 Prune-enriched Rosenbluth method: simulations of ${\it\theta}$ polymers of chain length up to 1000 000. Phys. Rev. E 56, 3682–3693.Google Scholar
Grassberger, P. 2002 Go with the winners: a general Monte-Carlo strategy. Comput. Phys. Commun. 147, 64–70.CrossRefGoogle Scholar
Haynes, P. H. 2011 Transport and mixing of atmospheric pollutants. In Environmental Hazards: The Fluid Mechanics and Geophysics of Extreme Events (ed. Moffatt, H. K. & Shuckburgh, E. F.). World Scientific.Google Scholar
Haynes, P. H., Poet, D. & Shuckburgh, E. F. 2007 Transport and mixing in dynamically consistent flows. J. Atmos. Sci. 64, 3640–3651.Google Scholar
Haynes, P. H. & Vanneste, J. 2014 Dispersion in the large-deviation regime. Part I. Shear flows and periodic flows. J. Fluid Mech. 745, 321–350.Google Scholar
Hourdin, F. & Talagrand, O. 2006 Eulerian backtracking of atmospheric tracers. I: Adjoint derivation and parametrization of subgrid-scale transport. Q. J. R. Meteorol. Soc. 132, 567–583.Google Scholar
Jones, A. R., Thomson, D. J., Hort, M. & Devenish, B. 2007 The UK Met Office’s next-generation atmospheric dispersion model, NAME III. In Air Pollution Modeling and its Application XVII (Proceedings of the 27th NATO/CCMS International Technical Meeting on Air Pollution Modelling and its Application) (ed. Borrego, C. & Norman, A.-L.), pp. 580–589. Springer.Google Scholar
Kloeden, P. E. & Platen, E. 1992 Numerical Solution of Stochastic Differential Equations, 4th edn. Springer.Google Scholar
Majda, A. J. & Kramer, P. R. 1999 Simplified models for turbulent diffusion: theory, numerical modelling and physical phenomena. Phys. Rep. 314, 237–574.Google Scholar
Methven, J., Arnold, S. R., Stohl, A., Evans, M. J., Avery, M., Law, K., Lewis, A. C., Monks, P. S., Parrish, D. D., Reeves, C., Schlager, H., Atlas, E., Blake, D. R., Coe, H., Crosier, J., Flocke, F. M., Holloway, J. S., Hopkins, J. R., McQuaid, J., Purvis, R., Rappengluck, B., Singh, H. B., Watson, N. M., Whalley, L. K. & Williams, P. I. 2006 Establishing Lagrangian connections between observations within air masses crossing the Atlantic during the ICARTT experiment. J. Geophys. Res. 111, D23S62.Google Scholar
Milstein, G. N. 1995 Numerical Solution of Stochastic Differential Equations. Kluwer.Google Scholar
Milstein, G. N., Schoenmakers, J. G. M. & Spokoiny, V. 2004 Transition density estimation for stochastic differential equations via forward–reverse representations. Bernoulli 10 (2), 281–312.CrossRefGoogle Scholar
Milstein, G. N. & Tretyakov, M. V. 2004 Stochastic Numerics for Mathematical Physics. Springer.Google Scholar
Øksendal, B. 2007 Stochastic Differential Equations: An Introduction with Applications, 6th edn. Springer.Google Scholar
Pierrehumbert, R. T. 1991 Chaotic mixing of tracer and vorticity by modulated travelling Rossby waves. Geophys. Astrophys. Fluid Dyn. 58, 285–319.Google Scholar
Plumb, R. A. 2002 Stratospheric transport. J. Met. Soc. Japan 80, 793–809.Google Scholar
Proehl, J. A., Lynch, D. R., McGillicuddy, D. J. Jr & Ledwell, J. R. 2005 Modeling turbulent dispersion on the north flank of Georges Bank using Lagrangian particle methods. Cont. Shelf Res. 25, 875–900.CrossRefGoogle Scholar
Rodean, H. C. 1996 Stochastic Lagrangian Models of Turbulent Diffusion. American Meteorological Society.CrossRefGoogle Scholar
Silverman, B. W. 1986 Density Estimation for Statistics and Data Analysis. Chapman and Hall.Google Scholar
Spivakovskaya, D., Heemink, A. W. & Deleersnijder, E. 2007 Lagrangian modelling of multi-dimensional advection–diffusion with space-varying diffusivities: theory and idealized test cases. Ocean Dyn. 57, 189–203.Google Scholar
Spivakovskaya, D., Heemink, A., Milstein, G. & Schoenmakers, J. 2005 Simulation of the transport of particles in coastal waters using forward and reverse time diffusion. Adv. Water Resour. 28 (9), 927–938.Google Scholar
Stohl, A., Forster, C., Frank, A., Seibert, P. & Wotawa, G. 2005 Technical note: the Lagrangian particle dispersion model FLEXPART version 6.2. Atmos. Chem. Phys. 5, 2461–2474.Google Scholar
Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Thomson, D. J. 1987 Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 180, 529–556.Google Scholar
Tocino, A. & Ardanuy, R. 2002 Runge–Kutta methods for numerical solution of stochastic differential equations. J. Comput. Appl. Maths 138, 219–241.CrossRefGoogle Scholar
Vanden-Eijnden, E. & Weare, J. 2012 Rare event simulation for small noise diffusions. Commun. Pure Appl. Maths 65, 1770–1803.Google Scholar
Wand, M. P. & Jones, M. C. 1994 Kernel Smoothing. Chapman and Hall.Google Scholar
Weiss, J. B. & Knobloch, E. 1989 Mass transport by modulated travelling waves. Phys. Rev. A 40, 2579–2589.Google Scholar
Weiss, J. B. & Provenzale, A. 2008 Transport and Mixing in Geophysical Flows. Springer.Google Scholar
Zimmermann, S., Koumoutsakos, P. & Kinzelbach, W. 2001 Simulation of pollutant transport using a particle method. J. Comput. Phys. 173 (1), 322–347.Google Scholar