Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhao, Chen
Yu, Tian
Zhou, Jiajia
and
Doi, Masao
2021.
Wetting Dynamics in an Angular Channel.
Langmuir,
Vol. 37,
Issue. 38,
p.
11276.
Doi, Masao
2021.
Onsager principle in polymer dynamics.
Progress in Polymer Science,
Vol. 112,
Issue. ,
p.
101339.
McCraney, Joshua
Weislogel, Mark
and
Steen, Paul
2021.
The draining of capillary liquids from containers with interior corners aboard the ISS.
npj Microgravity,
Vol. 7,
Issue. 1,
Yu, Tian
Sun, Qicheng
Zhao, Chen
Zhou, Jiajia
and
Doi, Masao
2021.
Wetting equilibrium in a rectangular channel.
Soft Matter,
Vol. 17,
Issue. 13,
p.
3594.
Zhao, Chen
Zhou, Jiajia
and
Doi, Masao
2022.
Capillary Rising in a Tube with Corners.
Langmuir,
Vol. 38,
Issue. 18,
p.
5779.
Chen, Shangtong
Duan, Li
Li, Yong
Ding, Fenglin
Liu, Jintao
and
Li, Wen
2022.
Capillary Phenomena Between Plates from Statics to Dynamics Under Microgravity.
Microgravity Science and Technology,
Vol. 34,
Issue. 4,
Cai, Jianchao
Chen, Yin
Liu, Yang
Li, Shuang
and
Sun, Chenhao
2022.
Capillary imbibition and flow of wetting liquid in irregular capillaries: A 100-year review.
Advances in Colloid and Interface Science,
Vol. 304,
Issue. ,
p.
102654.
Li, Yuan
Sanfilippo, Joseph E.
Kearns, Daniel
Yang, Judy Q.
and
Steven, Blaire
2022.
Corner Flows Induced by Surfactant-Producing Bacteria Bacillus subtilis and Pseudomonas fluorescens.
Microbiology Spectrum,
Vol. 10,
Issue. 5,
Kubochkin, Nikolai
and
Gambaryan-Roisman, Tatiana
2022.
Capillary-driven flow in corner geometries.
Current Opinion in Colloid & Interface Science,
Vol. 59,
Issue. ,
p.
101575.
Chen, Shangtong
Wu, Di
Li, Yong
Liu, Jintao
Duan, Li
and
Li, Wen
2022.
Profiles of Liquid on the Surface of Revolution with Varying Cross-section under Microgravity.
Microgravity Science and Technology,
Vol. 34,
Issue. 6,
Van Hulle, J.
and
Vandewalle, N.
2023.
Effect of groove curvature on droplet spreading.
Soft Matter,
Vol. 19,
Issue. 25,
p.
4669.
Miao, Weining
Tian, Shihao
Yuan, Quanzi
Tian, Ye
and
Jiang, Lei
2023.
Direct observation of spreading precursor liquids in a corner.
National Science Review,
Vol. 10,
Issue. 7,
Chen, Guan-Lin
He, Guan-Yu
Sheng, Yu-Jane
and
Tsao, Heng-Kwong
2023.
Imbibition Dynamics in a U-Groove Microchannel with Sudden Enlargement.
Langmuir,
Vol. 39,
Issue. 31,
p.
10993.
Chen, Shangtong
Guo, Lei
Li, Yong
Liu, Jintao
Kang, Qi
and
Li, Wen
2023.
Capillary-driven flows in eccentric annuli under microgravity.
Archive of Applied Mechanics,
Vol. 93,
Issue. 2,
p.
731.
Chen, Shangtong
Zhang, Chu
Li, Wen
Li, Yong
Ding, Fenglin
and
Kang, Qi
2023.
Capillary phenomena in the corner of truncated-cone-shaped containers under microgravity.
Acta Mechanica Sinica,
Vol. 39,
Issue. 1,
Suo, Si
2024.
Spontaneous imbibition of a liquid film wetting a wall-mounted cylinder corner.
Soft Matter,
Vol. 20,
Issue. 3,
p.
578.
Atre, Chitransh
Manoj, Aditya
and
Puthenveettil, Baburaj A.
2024.
Fluid Mechanics and Fluid Power, Volume 5.
p.
327.
Yu, Jiahui
Zhao, Rui
Wang, Jine
Wang, Nü
Xu, Jiujun
Jin, Meihua
and
Zhao, Yong
2024.
Earthworm skin inspired rapid secretion of continuous liquid slippery film via nanochannels.
Tribology International,
Vol. 192,
Issue. ,
p.
109220.
Chen, Shangtong
Gao, Yong
Li, Wen
Ding, Fenglin
and
Li, Yong
2024.
Profiles of Static Liquid–Gas Interfaces in Axisymmetric Containers with Different Accelerations.
Langmuir,
Vol. 40,
Issue. 16,
p.
8617.
Wu, Katie
Duprat, C.
and
Stone, H.A.
2024.
Capillary rise in sharp corners: not quite universal.
Journal of Fluid Mechanics,
Vol. 978,
Issue. ,
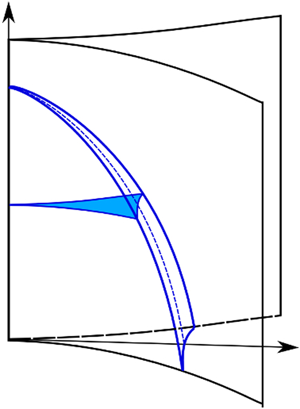
 $y=cx^n$ with
$y=cx^n$ with  $n \ge 1$. Using the Onsager principle, we derive a partial differential equation that describes the time evolution of the meniscus profile. By solving the equation both numerically and analytically, we show that the capillary rising dynamics is quite universal. Our theory explains the surprising finding by Ponomarenko et al. (J. Fluid Mech., vol. 666, 2011, pp. 146–154) that the time dependence of the height not only obeys the universal power-law of
$n \ge 1$. Using the Onsager principle, we derive a partial differential equation that describes the time evolution of the meniscus profile. By solving the equation both numerically and analytically, we show that the capillary rising dynamics is quite universal. Our theory explains the surprising finding by Ponomarenko et al. (J. Fluid Mech., vol. 666, 2011, pp. 146–154) that the time dependence of the height not only obeys the universal power-law of  $t^{1/3}$, but also that the prefactor is almost independent of
$t^{1/3}$, but also that the prefactor is almost independent of  $n$.
$n$.



