No CrossRef data available.
Article contents
Unifying constitutive law of vibroconvective turbulence in microgravity
Published online by Cambridge University Press: 16 May 2024
Abstract
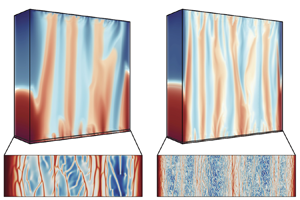
We report the unified constitutive law of vibroconvective turbulence in microgravity, i.e.  $Nu \sim a^{-1} Re_{os}^\beta$ where the Nusselt number
$Nu \sim a^{-1} Re_{os}^\beta$ where the Nusselt number  $Nu$ measures the global heat transport,
$Nu$ measures the global heat transport,  $a$ is the dimensionless vibration amplitude,
$a$ is the dimensionless vibration amplitude,  $Re_{os}$ is the oscillational Reynolds number and
$Re_{os}$ is the oscillational Reynolds number and  $\beta$ is the universal exponent. We find that the dynamics of boundary layers plays an essential role in vibroconvective heat transport and the
$\beta$ is the universal exponent. We find that the dynamics of boundary layers plays an essential role in vibroconvective heat transport and the  $Nu$-scaling exponent
$Nu$-scaling exponent  $\beta$ is determined by the competition between the thermal boundary layer (TBL) and vibration-induced oscillating boundary layer (OBL). Then a physical model is proposed to explain the change of scaling exponent from
$\beta$ is determined by the competition between the thermal boundary layer (TBL) and vibration-induced oscillating boundary layer (OBL). Then a physical model is proposed to explain the change of scaling exponent from  $\beta =2$ in the TBL-dominant regime to
$\beta =2$ in the TBL-dominant regime to  $\beta = 4/3$ in the OBL-dominant regime. Our finding elucidates the emergence of universal constitutive laws in vibroconvective turbulence, and opens up a new avenue for generating a controllable effective heat transport under microgravity or even microfluidic environment in which the gravity effect is nearly absent.
$\beta = 4/3$ in the OBL-dominant regime. Our finding elucidates the emergence of universal constitutive laws in vibroconvective turbulence, and opens up a new avenue for generating a controllable effective heat transport under microgravity or even microfluidic environment in which the gravity effect is nearly absent.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press





