Article contents
Travelling wave states in pipe flow
Published online by Cambridge University Press: 22 February 2016
Abstract
In this paper, we have found two new nonlinear travelling wave solutions in pipe flows. We investigate possible asymptotic structures at large Reynolds number 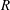 $R$ when wavenumber is independent of
$R$ when wavenumber is independent of 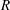 $R$ and identify numerically calculated solutions as finite
$R$ and identify numerically calculated solutions as finite 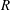 $R$ realizations of a nonlinear viscous core (NVC) state that collapses towards the pipe centre with increasing
$R$ realizations of a nonlinear viscous core (NVC) state that collapses towards the pipe centre with increasing  $R$ at a rate
$R$ at a rate 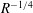 $R^{-1/4}$. We also identify previous numerically calculated states as finite
$R^{-1/4}$. We also identify previous numerically calculated states as finite 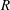 $R$ realizations of a vortex wave interacting (VWI) state with an asymptotic structure similar to the ones in channel flows studied earlier by Hall & Sherwin (J. Fluid Mech., vol. 661, 2010, pp. 178–205). In addition, asymptotics suggests the possibility of a VWI state that collapses towards the pipe centre like
$R$ realizations of a vortex wave interacting (VWI) state with an asymptotic structure similar to the ones in channel flows studied earlier by Hall & Sherwin (J. Fluid Mech., vol. 661, 2010, pp. 178–205). In addition, asymptotics suggests the possibility of a VWI state that collapses towards the pipe centre like 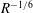 $R^{-1/6}$, though this remains to be confirmed numerically.
$R^{-1/6}$, though this remains to be confirmed numerically.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 11
- Cited by





