Article contents
Suspension flow through an asymmetric T-junction
Published online by Cambridge University Press: 04 April 2018
Abstract
The flow of a suspension through a bifurcating channel is studied experimentally and by computational methods. The geometry considered is an ‘asymmetric T’, as flow in the entering branch divides to either continue straight or to make a right angle turn. All branches are of the same square cross-section of side length 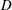 $D$, with inlet and outlet section lengths
$D$, with inlet and outlet section lengths 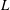 $L$ yielding
$L$ yielding 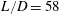 $L/D=58$ in the experiments. The suspensions are composed of neutrally buoyant spherical particles in a Newtonian liquid, with mean particle diameters of
$L/D=58$ in the experiments. The suspensions are composed of neutrally buoyant spherical particles in a Newtonian liquid, with mean particle diameters of 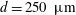 $d=250~\unicode[STIX]{x03BC}\text{m}$ and
$d=250~\unicode[STIX]{x03BC}\text{m}$ and 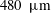 $480~\unicode[STIX]{x03BC}\text{m}$ resulting in
$480~\unicode[STIX]{x03BC}\text{m}$ resulting in 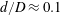 $d/D\approx 0.1$ to
$d/D\approx 0.1$ to 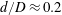 $d/D\approx 0.2$ for
$d/D\approx 0.2$ for 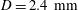 $D=2.4~\text{mm}$. The flow rate ratio
$D=2.4~\text{mm}$. The flow rate ratio 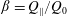 $\unicode[STIX]{x1D6FD}=Q_{\Vert }/Q_{0}$, defined for the bulk, fluid and particles, is used to characterize the flow behaviour; here
$\unicode[STIX]{x1D6FD}=Q_{\Vert }/Q_{0}$, defined for the bulk, fluid and particles, is used to characterize the flow behaviour; here 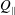 $Q_{\Vert }$ and
$Q_{\Vert }$ and 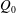 $Q_{0}$ are volumetric flow rates in the straight outlet branch and inlet branch, respectively. The channel Reynolds number
$Q_{0}$ are volumetric flow rates in the straight outlet branch and inlet branch, respectively. The channel Reynolds number 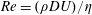 $Re=(\unicode[STIX]{x1D70C}DU)/\unicode[STIX]{x1D702}$ was varied over
$Re=(\unicode[STIX]{x1D70C}DU)/\unicode[STIX]{x1D702}$ was varied over 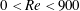 $0<Re<900$, with
$0<Re<900$, with 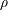 $\unicode[STIX]{x1D70C}$ and
$\unicode[STIX]{x1D70C}$ and 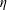 $\unicode[STIX]{x1D702}$ the fluid density and viscosity, respectively, and
$\unicode[STIX]{x1D702}$ the fluid density and viscosity, respectively, and 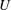 $U$ the mean velocity in the inlet channel; the inlet particle volume fraction was
$U$ the mean velocity in the inlet channel; the inlet particle volume fraction was 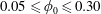 $0.05\leqslant \unicode[STIX]{x1D719}_{0}\leqslant 0.30$. Experimental and numerical results for single-phase Newtonian fluid both show
$0.05\leqslant \unicode[STIX]{x1D719}_{0}\leqslant 0.30$. Experimental and numerical results for single-phase Newtonian fluid both show 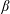 $\unicode[STIX]{x1D6FD}$ increasing with
$\unicode[STIX]{x1D6FD}$ increasing with 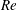 $Re$, implying more material tending toward the straight branch as the inertia of the flow increases. In suspension flow at small
$Re$, implying more material tending toward the straight branch as the inertia of the flow increases. In suspension flow at small 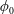 $\unicode[STIX]{x1D719}_{0}$, inertial migration of particles in the inlet branch affects the flow rate ratio for particles (
$\unicode[STIX]{x1D719}_{0}$, inertial migration of particles in the inlet branch affects the flow rate ratio for particles (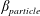 $\unicode[STIX]{x1D6FD}_{\mathit{particle}}$) and suspension (
$\unicode[STIX]{x1D6FD}_{\mathit{particle}}$) and suspension (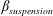 $\unicode[STIX]{x1D6FD}_{\mathit{suspension}}$). The flow split for the bulk suspension satisfies
$\unicode[STIX]{x1D6FD}_{\mathit{suspension}}$). The flow split for the bulk suspension satisfies 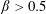 $\unicode[STIX]{x1D6FD}>0.5$ for
$\unicode[STIX]{x1D6FD}>0.5$ for 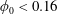 $\unicode[STIX]{x1D719}_{0}<0.16$ while
$\unicode[STIX]{x1D719}_{0}<0.16$ while 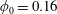 $\unicode[STIX]{x1D719}_{0}=0.16$ crosses from
$\unicode[STIX]{x1D719}_{0}=0.16$ crosses from 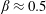 $\unicode[STIX]{x1D6FD}\approx 0.5$ to
$\unicode[STIX]{x1D6FD}\approx 0.5$ to 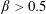 $\unicode[STIX]{x1D6FD}>0.5$ at
$\unicode[STIX]{x1D6FD}>0.5$ at 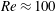 $Re\approx 100$. For
$Re\approx 100$. For 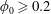 $\unicode[STIX]{x1D719}_{0}\geqslant 0.2$,
$\unicode[STIX]{x1D719}_{0}\geqslant 0.2$, 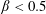 $\unicode[STIX]{x1D6FD}<0.5$ at all
$\unicode[STIX]{x1D6FD}<0.5$ at all  $Re$ studied. A complex dependence of the mean solid fraction in the downstream branches upon inlet fraction
$Re$ studied. A complex dependence of the mean solid fraction in the downstream branches upon inlet fraction 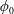 $\unicode[STIX]{x1D719}_{0}$ and
$\unicode[STIX]{x1D719}_{0}$ and  $Re$ is observed: for
$Re$ is observed: for 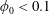 $\unicode[STIX]{x1D719}_{0}<0.1$, the solid fraction in the straight downstream branch initially decreases with
$\unicode[STIX]{x1D719}_{0}<0.1$, the solid fraction in the straight downstream branch initially decreases with 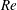 $Re$, before increasing to surpass the inlet fraction at large
$Re$, before increasing to surpass the inlet fraction at large 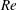 $Re$ (
$Re$ (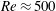 $Re\approx 500$ for
$Re\approx 500$ for 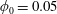 $\unicode[STIX]{x1D719}_{0}=0.05$). At
$\unicode[STIX]{x1D719}_{0}=0.05$). At 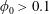 $\unicode[STIX]{x1D719}_{0}>0.1$, the solid fraction in the straight branch satisfies
$\unicode[STIX]{x1D719}_{0}>0.1$, the solid fraction in the straight branch satisfies 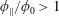 $\unicode[STIX]{x1D719}_{\Vert }/\unicode[STIX]{x1D719}_{0}>1$, and this ratio grows with
$\unicode[STIX]{x1D719}_{\Vert }/\unicode[STIX]{x1D719}_{0}>1$, and this ratio grows with 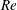 $Re$. Discrete-particle simulations employing immersed boundary and lattice-Boltzmann techniques are used to analyse these phenomena, allowing rationalization of aspects of this complex behaviour as being due to particle migration in the inlet branch.
$Re$. Discrete-particle simulations employing immersed boundary and lattice-Boltzmann techniques are used to analyse these phenomena, allowing rationalization of aspects of this complex behaviour as being due to particle migration in the inlet branch.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Manoorkar et al. supplementary movie 1
Experiment at Φ0 = 0.05, d/D = 0.2, Re = 200. Video is 100 times slower than real time.
Manoorkar et al. supplementary movie 2
Immersed boundary simulation at Φ0 = 0.05, d/D = 0.2, Re = 200."The video shows the entry and bifurcation regions separately as well as the full channel view as the particles enter and reach a steady state flow.
Manoorkar et al. supplementary movie 3
Comparison of experiment and immersed boundary simulation in bifurcation region at Φ0 = 0.05, d/D = 0.2, Re = 300 for IB and Re = 311 for experiments.
Manoorkar et al. supplementary movie 4
Experiment at Φ0 = 0.05, d/D = 0.2, Re = 415. Video is 100 times slower than real time.
- 10
- Cited by




