Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T12:26:11.566Z Has data issue: false hasContentIssue false
  • English
  • Français

Stabilizing/destabilizing the large-scale circulation in turbulent Rayleigh–Bénard convection with sidewall temperature control

Published online by Cambridge University Press:  09 March 2021

Shengqi Zhang Open the ORCID record for Shengqi Zhang [Opens in a new window] ,
Xin Chen Open the ORCID record for Xin Chen [Opens in a new window] ,
Zhenhua Xia Open the ORCID record for Zhenhua Xia [Opens in a new window] ,
Heng-Dong Xi Open the ORCID record for Heng-Dong Xi [Opens in a new window] ,
Quan Zhou Open the ORCID record for Quan Zhou [Opens in a new window]  and
Shiyi Chen Open the ORCID record for Shiyi Chen [Opens in a new window]
Shengqi Zhang
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Peking University, Beijing100871, PR China
Xin Chen
Affiliation:
Institute of Extreme Mechanics and School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, PR China
Zhenhua Xia*
Affiliation:
Department of Engineering Mechanics, Zhejiang University, Hangzhou310027, PR China
Heng-Dong Xi
Affiliation:
Institute of Extreme Mechanics and School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, PR China
Quan Zhou
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai200072, PR China
Shiyi Chen*
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Peking University, Beijing100871, PR China Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen518055, PR China
*
†Email addresses for correspondence: xiazh@zju.edu.cn, chensy@sustech.edu.cn
†Email addresses for correspondence: xiazh@zju.edu.cn, chensy@sustech.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

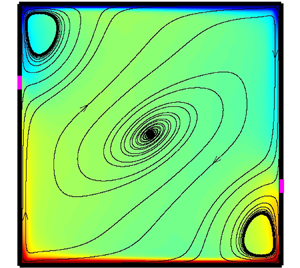
In this paper, we designed two different configurations with locally isothermal sidewalls, where the temperature is set to be the bulk temperature, to control the large-scale circulation in turbulent Rayleigh–Bénard convection, namely two-point control and four-point control. At fixed Rayleigh number $Ra=10^8$ and Prandtl number $Pr=2$, a series of direct numerical simulations are performed on both two-dimensional (2-D) and quasi-two-dimensional (quasi-2-D) cavities with both types of control, where the width of the control area is fixed at $\delta _c=0.05$ and the vertical distance from the cavity centre $h_c$ varies from 0 to 0.45 with an interval of 0.05. Our results show that the control effect depends on $h_c$, the control configurations as well as the flow dimensions. For 2-D cavities, both two-point control and four-point control suppress the flow reversal when $h_c \geq 0.05$, accompanied by the enhancement of vertical heat transfer and the strength of the large-scale circulation. For quasi-2-D cavities, the suppression of the flow reversals is obvious with two-point control and $h_c\geq 0.05$, while the effect is rather limited with four-point control. Further experiments with $Pr=5.7$ and $Ra$ up to $7.36\times10^8$ show that two-point control with $h_c=0.15$ can effectively suppress the flow reversal, while two-point control with $h_c=0$ can suppress the reversals at low $Ra=1.93\times 10^8$ and activate them at higher $Ra=7.36\times 10^8$, which agrees well with our numerical simulations.

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A14
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Araujo, F.F., Grossmann, S. & Lohse, D. 2005 Wind reversals in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084502.CrossRefGoogle ScholarPubMed
Assaf, M., Angheluta, L. & Goldenfeld, N. 2011 Rare fluctuations and large-scale circulation cessations in turbulent convection. Phys. Rev. Lett. 107, 044502.CrossRefGoogle ScholarPubMed
Benzi, R. 2005 Flow reversal in a simple dynamical model of turbulence. Phys. Rev. Lett. 95, 024502.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2007 Large-scale circulation model for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 134501.CrossRefGoogle ScholarPubMed
Brown, E. & Ahlers, G. 2008 a Azimuthal asymmetries of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20 (10), 105105.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2008 b A model of diffusion in a potential well for the dynamics of the large-scale circulation in turbulent Rayleigh—Bénard convection. Phys. Fluids 20, 075101.CrossRefGoogle Scholar
Brown, E., Funfschilling, D. & Ahlers, G. 2007 Anomalous Reynolds-number scaling in turbulent Rayleigh–Bénard convection. J. Stat. Mech.-Theory Exp. 2007 (10), P10005.CrossRefGoogle Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.CrossRefGoogle ScholarPubMed
Castillo-Castellanos, A., Sergent, A., Podvin, B. & Rossi, M. 2019 Cessation and reversals of large-scale structures in square Rayleigh–Bénard cells. J. Fluid Mech. 877, 922–954.CrossRefGoogle Scholar
Chandra, M. & Verma, M.K. 2011 Dynamics and symmetries of flow reversals in turbulent convection. Phys. Rev. E 83, 067303.CrossRefGoogle ScholarPubMed
Chandra, M. & Verma, M.K. 2013 Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett. 110, 114503.CrossRefGoogle ScholarPubMed
Chen, X., Huang, S.-D., Xia, K.-Q. & Xi, H.-D. 2019 Emergence of substructures inside the large-scale circulation induces transition in flow reversals in turbulent thermal convection. J. Fluid Mech. 877, R1.CrossRefGoogle Scholar
Chen, X., Wang, D.-P. & Xi, H.-D. 2020 Reduced flow reversals in turbulent convection in the absence of corner vortices. J. Fluid Mech. 891, R5.CrossRefGoogle Scholar
Chong, K.L., Wagner, S., Kaczorowski, M., Shishkina, O. & Xia, K.-Q. 2018 Effect of Prandtl number on heat transport enhancement in Rayleigh–Bénard convection under geometrical confinement. Phys. Rev. Fluids 3, 013501.CrossRefGoogle Scholar
Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh—Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.CrossRefGoogle Scholar
van Doorn, E., Dhruva, B., Sreenivasan, K.R. & Cassella, V. 2000 Statistics of wind direction and its increments. Phys. Fluids 12 (6), 1529–1534.CrossRefGoogle Scholar
Glatzmaiers, G.A. & Roberts, P.H. 1995 A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 377 (6546), 203–209.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.CrossRefGoogle ScholarPubMed
Hartmann, D.L., Moy, L.A. & Fu, Q. 2001 Tropical convection and the energy balance at the top of the atmosphere. J. Climate 14 (24), 4495–4511.2.0.CO;2>CrossRefGoogle Scholar
Huang, S.-D., Wang, F., Xi, H.-D. & Xia, K.-Q. 2015 Comparative experimental study of fixed temperature and fixed heat flux boundary conditions in turbulent thermal convection. Phys. Rev. Lett. 115, 154502.CrossRefGoogle ScholarPubMed
Huang, S.-D. & Xia, K.-Q. 2016 Effects of geometric confinement in quasi-2-d turbulent Rayleigh–Bénard convection. J. Fluid Mech. 794, 639–654.CrossRefGoogle Scholar
Kooij, G., Botchev, M., Frederix, E., Geurts, B., Horn, S., Lohse, D., van der Poel, E., Shishkina, O., Stevens, R.J. & Verzicco, R. 2018 Comparison of computational codes for direct numerical simulations of turbulent Rayleigh–Bénard convection. Comput. Fluids 166, 1–8.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Ni, R., Huang, S.-D. & Xia, K.-Q. 2015 Reversals of the large-scale circulation in quasi-2D Rayleigh–Bénard convection. J. Fluid Mech. 778, R5.CrossRefGoogle Scholar
Petschel, K., Wilczek, M., Breuer, M., Friedrich, R. & Hansen, U. 2011 Statistical analysis of global wind dynamics in vigorous Rayleigh–Bénard convection. Phys. Rev. E 84, 026309.CrossRefGoogle ScholarPubMed
Podvin, B. & Sergent, A. 2015 A large-scale investigation of wind reversal in a square Rayleigh–Bénard cell. J. Fluid Mech. 766, 172–201.CrossRefGoogle Scholar
Qiu, X.-L., Xia, K.-Q. & Tong, P. 2005 Experimental study of velocity boundary layer near a rough conducting surface in turbulent natural convection. J. Turbul. 6, N30.CrossRefGoogle Scholar
Sreenivasan, K., Bershadskii, A. & Niemela, J.J. 2002 Mean wind and its reversal in thermal convection. Phys. Rev. E 65, 056306.CrossRefGoogle ScholarPubMed
Stevens, R.J., Lohse, D. & Verzicco, R. 2014 Sidewall effects in Rayleigh–Bénard convection. J. Fluid Mech. 741, 1–27.CrossRefGoogle Scholar
Sugiyama, K., Ni, R., Stevens, R.J., Chan, T.S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.CrossRefGoogle ScholarPubMed
Sun, C., Xi, H.-D. & Xia, K.-Q. 2005 Azimuthal symmetry, flow dynamics, and heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett. 95, 074502.CrossRefGoogle Scholar
Tsuji, Y., Mizuno, T., Mashiko, T. & Sano, M. 2005 Mean wind in convective turbulence of mercury. Phys. Rev. Lett. 94, 034501.CrossRefGoogle ScholarPubMed
Van Der Poel, E.P., Ostilla-Mónico, R., Donners, J. & Verzicco, R. 2015 A pencil distributed finite difference code for strongly turbulent wall-bounded flows. Comput. Fluids 116, 10–16.CrossRefGoogle Scholar
Vasil'ev, A. & Frick, P.G. 2011 Reversals of large-scale circulation in turbulent convection in rectangular cavities. J. Expl Theor. Phys. 93, 330–334.CrossRefGoogle Scholar
Wagner, S. & Shishkina, O. 2013 Aspect-ratio dependency of Rayleigh–Bénard convection in box-shaped containers. Phys. Fluids 25, 085110.CrossRefGoogle Scholar
Wan, Z.H., Wei, P., Verzicco, R., Lohse, D., Ahlers, G. & Stevens, R.J. 2019 Effect of sidewall on heat transfer and flow structure in Rayleigh–Bénard convection. J. Fluid Mech. 881, 218–243.CrossRefGoogle Scholar
Wang, Q., Xia, S.-N., Wang, B.-F., Sun, D.-J., Zhou, Q. & Wan, Z.-H. 2018 Flow reversals in two-dimensional thermal convection in tilted cells. J. Fluid Mech. 849, 355–372.CrossRefGoogle Scholar
Wang, Q., Xu, B.-L., Xia, S.-N., Wan, Z.-H. & Sun, D.-J. 2017 Thermal convection in a tilted rectangular cell with aspect ratio 0.5. Chin. Phys. Lett. 34, 104401.CrossRefGoogle Scholar
Wang, B.-F., Zhou, Q. & Sun, C. 2020 Vibration-induced boundary-layer destabilization achieves massive heat-transport enhancement. Sci. Adv. 6, eaaz8239.CrossRefGoogle ScholarPubMed
Xi, H.-D. & Xia, K.-Q. 2007 Cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E 75, 066307.CrossRefGoogle ScholarPubMed
Xi, H.-D. & Xia, K.-Q. 2008 Azimuthal motion, reorientation, cessation, and reversal of the large-scale circulation in turbulent thermal convection: a comparative study in aspect ratio one and one-half geometries. Phys. Rev. E 78, 036326.CrossRefGoogle ScholarPubMed
Xia, S.-N., Wan, Z.-H., Liu, S., Wang, Q. & Sun, D.-J. 2016 Flow reversals in Rayleigh–Bénard convection with non-Oberbeck–Boussinesq effects. J. Fluid Mech. 798, 628–642.CrossRefGoogle Scholar
Zhang, Y.-Z., Sun, C., Bao, Y. & Zhou, Q. 2018 How surface roughness reduces heat transport for small roughness heights in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 836, R2.CrossRefGoogle Scholar
Zhang, S., Xia, Z., Zhou, Q. & Chen, S. 2020 Controlling flow reversal in two-dimensional Rayleigh–Bénard convection. J. Fluid Mech. 891, R4.CrossRefGoogle Scholar
Zhu, X., Stevens, R.J.A.M., Shishkina, O., Verzicco, R. & Lohse, D. 2019 $Nu\sim Ra^{1/2}$ scaling enabled by multiscale wall roughness in Rayleigh–Bénard turbulence. J. Fluid Mech. 869, R4.CrossRefGoogle Scholar