Article contents
Resolvent-based study of compressibility effects on supersonic turbulent boundary layers
Published online by Cambridge University Press: 26 November 2019
Abstract
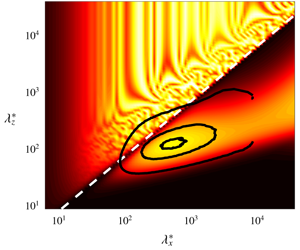
The resolvent formulation of McKeon & Sharma (J. Fluid Mech., vol. 658, 2010, pp. 336–382) is applied to supersonic turbulent boundary layers to study the validity of Morkovin’s hypothesis, which postulates that high-speed turbulence structures in zero-pressure-gradient turbulent boundary layers remain largely the same as their incompressible counterparts. Supersonic zero-pressure-gradient turbulent boundary layers with adiabatic wall boundary conditions at Mach numbers ranging from 2 to 4 are considered. Resolvent analysis highlights two distinct regions of the supersonic turbulent boundary layer in the wave parameter space: the relatively supersonic region and the relatively subsonic region. In the relatively supersonic region, where the flow is supersonic relative to the free-stream, resolvent modes display structures consistent with Mach wave radiation that are absent in the incompressible regime. In the relatively subsonic region, we show that the low-rank approximation of the resolvent operator is an effective approximation of the full system and that the response modes predicted by the model exhibit universal and geometrically self-similar behaviour via a transformation given by the semi-local scaling. Moreover, with the semi-local scaling, we show that the resolvent modes follow the same scaling law as their incompressible counterparts in this region, which has implications for modelling and the prediction of turbulent high-speed wall-bounded flows. We also show that the thermodynamic variables exhibit similar mode shapes to the streamwise velocity modes, supporting the strong Reynolds analogy. Finally, we demonstrate that the principal resolvent modes can be used to capture the energy distribution between momentum and thermodynamic fluctuations.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 20
- Cited by




