No CrossRef data available.
Article contents
Refraction of a triple-shock configuration at planar fast–slow gas interfaces
Published online by Cambridge University Press: 04 April 2024
Abstract
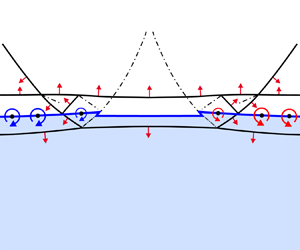
This paper characterizes the refraction of a triple-shock configuration at planar fast–slow gas interfaces. The primary objective is to reveal the wave configurations and elucidate the mechanisms governing circulation deposition and velocity perturbation on the interface caused by triple-shock refraction. The incident triple-shock configuration is generated by diffracting a planar shock around a rigid cylinder, and four interfaces with various  $Z_{{r}}$ (i.e. acoustic impedance ratio across the interface) are considered. An analytical model describing the triple-shock refraction is developed, which accurately predicts both the wave configurations as well as circulation deposition and velocity perturbation. Depending on
$Z_{{r}}$ (i.e. acoustic impedance ratio across the interface) are considered. An analytical model describing the triple-shock refraction is developed, which accurately predicts both the wave configurations as well as circulation deposition and velocity perturbation. Depending on  $Z_{{r}}$, three distinct patterns of transmitted waves can be anticipated: a triple-shock configuration; a four-shock configuration; a four-wave configuration. The underlying mechanism for the formation of these wave configurations is elucidated through shock polar analysis. A novel physical insight into the contribution of triple-shock refraction to the interface perturbation growth is provided. The results indicate that the reflected shock in an incident triple-shock configuration makes significant negative contribution to both circulation deposition and velocity perturbation. This investigation elucidates the underlying mechanism responsible for the relatively insignificant contribution of baroclinic circulation to the Richtmyer–Meshkov-like instability induced by a non-uniform shock, and provides an explanation for the decrease in growth rate of interface perturbation amplitude with increasing Atwood number.
$Z_{{r}}$, three distinct patterns of transmitted waves can be anticipated: a triple-shock configuration; a four-shock configuration; a four-wave configuration. The underlying mechanism for the formation of these wave configurations is elucidated through shock polar analysis. A novel physical insight into the contribution of triple-shock refraction to the interface perturbation growth is provided. The results indicate that the reflected shock in an incident triple-shock configuration makes significant negative contribution to both circulation deposition and velocity perturbation. This investigation elucidates the underlying mechanism responsible for the relatively insignificant contribution of baroclinic circulation to the Richtmyer–Meshkov-like instability induced by a non-uniform shock, and provides an explanation for the decrease in growth rate of interface perturbation amplitude with increasing Atwood number.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press





