Hostname: page-component-77c89778f8-gq7q9 Total loading time: 0 Render date: 2024-07-19T05:03:48.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-steady linked vortices with chaotic streamlines

Published online by Cambridge University Press:  14 October 2011

Oscar Velasco Fuentes  and
Angélica Romero Arteaga
Oscar Velasco Fuentes*
Affiliation:
Departamento de Oceanografía Física, CICESE, Ensenada, BC 22860, México
Angélica Romero Arteaga
Affiliation:
Departamento de Oceanografía Física, CICESE, Ensenada, BC 22860, México
*
†Email address for correspondence: ovelasco@cicese.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper describes the motion and the flow geometry of two or more linked ring vortices in an otherwise quiescent, ideal fluid. The vortices are thin tubes of near-circular shape which lie on the surface of an immaterial torus of small aspect ratio. Since the vortices are assumed to be identical and evenly distributed on any meridional section of the torus, the flow evolution depends only on the number of vortices () and the torus aspect ratio (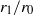, where 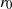is the centreline radius and 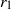is the cross-section radius). Numerical simulations based on the Biot–Savart law showed that a small number of vortices (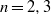) coiled on a thin torus (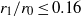) progressed along and rotated around the symmetry axis of the torus in an almost uniform manner while each vortex approximately preserved its shape. In the comoving frame the velocity field always possesses two stagnation points. The transverse intersection, along 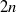streamlines, of the stream tube emanating from the front stagnation point and the stream tube ending at the rear stagnation point creates a three-dimensional chaotic tangle. It was found that the volume of the chaotic region increases with increasing torus aspect ratio and decreasing number of vortices.

JFM classification

Nonlinear Dynamical Systems: Chaos Vortex Flows: Vortex dynamics Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 687 , 25 November 2011 , pp. 571 - 583
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Baggaley, A. W. & Barenghi, C. F. 2011 Spectrum of turbulent Kelvin-waves cascade in superfluid helium. Phys. Rev. B 83 (13), 134509.CrossRefGoogle Scholar
2. Barenghi, C. F., Ricca, R. L. & Samuels, D. C. 2001 How tangled is a tangle? Physica D 157, 197–206.CrossRefGoogle Scholar
3. Helmholtz, H. 1858 Über Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen. J. Reine Angew. Math. 55, 25–55. English translation in Phil. Mag. 33 (1867), 485–512.Google Scholar
4. Kida, S. 1981 A vortex filament moving without change of form. J. Fluid Mech. 112, 397–409.CrossRefGoogle Scholar
5. Kimura, Y. & Koikari, S. 2004 Particle transport by a vortex soliton. J. Fluid Mech. 510, 201–218.CrossRefGoogle Scholar
6. Lamb, H. 1879 Treatise on the Mathematical Theory of the Motion of Fluids. Cambridge University Press.CrossRefGoogle Scholar
7. Maggioni, F., Alamri, S., Barenghi, C. F. & Ricca, R. L. 2010 Velocity, energy, and helicity of vortex knots and unknots. Phys. Rev. E 82 (2), 026309.CrossRefGoogle ScholarPubMed
8. Maxwell, J. C. & Harman, P. M. 1995 The Scientific Letters and Papers of James Clerk Maxwell: 1862–1873, vol. 2. Cambridge University Press. Letter to Peter Guthrie Tait, July 1868.Google Scholar
9. Ricca, R. L., Samuels, D. C. & Barenghi, C. F. 1999 Evolution of vortex knots. J. Fluid Mech. 391, 29–44.CrossRefGoogle Scholar
10. Rogers, W. B. 1858 On the formation of rotating rings by air and liquids under certain conditions of discharge. Am. J. Sci. Arts 26, 246–258.Google Scholar
11. Rom-Kedar, V., Leonard, A. & Wiggins, S. 1990 An analytical study of transport, mixing and chaos in an unsteady vortical flow. J. Fluid Mech. 214, 347–394.CrossRefGoogle Scholar
12. Romero Arteaga, A. 2011 Vórtices eslabonados cuasi-estacionarios. Master’s thesis, CICESE.Google Scholar
13. Saffman, P. G. 1995 Vortex Dynamics. Cambridge University Press.Google Scholar
14. Thompson, S. P. 1910 The Life of William Thomson Baron Kelvin of Largs, vol. 1. Macmillan.Google Scholar
15. Thomson, J. J. 1883 A Treatise on the Motion of Vortex Rings. Macmillan.Google Scholar
16. Thomson, W. (Lord Kelvin) 1867 On vortex atoms. Phil. Mag. 34, 15–24. Also in Mathematical and Physical Papers, vol. 4, pp. 1–12.CrossRefGoogle Scholar
17. Thomson, W. (Lord Kelvin) 1875 Vortex statics. Proc. R. Soc. Edin. 9, 59–73 Also in Mathematical and Physical Papers, vol. 4, pp. 115–128.CrossRefGoogle Scholar
18. Velasco Fuentes, O. 2010 Chaotic streamlines in the flow of knotted and unknotted vortices. Theor. Comput. Fluid Dyn. 24, 189–193.CrossRefGoogle Scholar
19. Wiggins, S. 1992 Chaotic Transport in Dynamical Systems. Springer.CrossRefGoogle Scholar