Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-23T09:11:56.462Z Has data issue: false hasContentIssue false
  • English
  • Français

Preferential frequency and size effect of the Brownian force acting on a nanoparticle

Published online by Cambridge University Press:  05 September 2017

Hanhui Jin Open the ORCID record for Hanhui Jin [Opens in a new window] ,
Ningning Liu ,
Xiaoke Ku  and
Jianren Fan Open the ORCID record for Jianren Fan [Opens in a new window]
Hanhui Jin
Affiliation:
School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, PR China Collaborative Innovation Center of Advanced Aero-Engine, Hangzhou 310027, PR China
Ningning Liu
Affiliation:
School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, PR China
Xiaoke Ku*
Affiliation:
School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, PR China
Jianren Fan
Affiliation:
State Key Laboratory of Clean Energy Utilization, Zhejiang University, Hangzhou 310027, PR China
*
†Email address for correspondence: xiaokeku@zju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

The Brownian motion of a nanoparticle in fluid depends on the molecular forces acting on it. Because of the small size and the high frequency, it is difficult to make experimental measurements of these forces. In the present work, Brownian forces acting on a nanoparticle are numerically investigated with the molecular dynamics method. Some new phenomena are disclosed. (i) The probability distribution shows that the Brownian forces conform to the Gaussian distribution and self-similarity of the probability distribution is also found for different 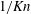$1/Kn$ numbers which are characterized with the particle radius and the mean path 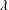$\unicode[STIX]{x1D706}$ of the gas molecule 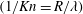$(1/Kn=R/\unicode[STIX]{x1D706})$. (ii) The frequency spectrum distribution of the Brownian force is not a white noise spectrum, which is different from the assumption commonly used in Langevin model. The preferential frequency of the Brownian force is found. (iii) The size effect relating to the Brownian forces is not monotonically varying with 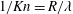$1/Kn=R/\unicode[STIX]{x1D706}$ and is also found. It first increases and then decreases after it reaches the maximum value at 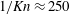$1/Kn\approx 250$. The variation process for 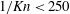$1/Kn<250$ observed in the present work has not been reported in previous research to date.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Rarefied Gas Flow: Molecular dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , pp. 648 - 660
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beeman, D. 1976 Some multistep methods for use in molecular dynamics calculations. J. Comput. Phys. 20 (2), 130–139.Google Scholar
Berendsen, H. J., Postma, J. V., van Gunsteren, W. F., Dinola, A. R. H. J. & Haak, J. R. 1984 Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81 (8), 3684–3690.Google Scholar
Berna, J., Leigh, D. A., Lubomska, M., Mendoza, S. M., Pérez, E. M., Rudolf, P. & Zerbetto, F. 2005 Macroscopic transport by synthetic molecular machines. Nat. Mater. 4 (9), 704–710.CrossRefGoogle ScholarPubMed
Blum, J., Bruns, S., Rademacher, D., Voss, A., Willenberg, B. & Krause, M. 2006 Measurement of the translational and rotational brownian motion of individual particles in a rarefied gas. Phys. Rev. Lett. 97 (23), 230601.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.CrossRefGoogle Scholar
Cleri, F. & Rosato, V. 1993 Tight-binding potentials for transition metals and alloys. Phys. Rev. B 48 (1), 22.Google Scholar
Einstein, A. 1905 Über die von der molekularkinetischen theorie der wärme geforderte bewegung von in ruhenden flüssigkeiten suspendierten teilchen. Ann. Phys. 322 (8), 549–560.CrossRefGoogle Scholar
Ermak, D. L. & McCammon, J. A. 1978 Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 69 (4), 1352–1360.CrossRefGoogle Scholar
Han, Y., Alsayed, A. M., Nobili, M., Zhang, J., Lubensky, T. C. & Yodh, A. G. 2006 Brownian motion of an ellipsoid. Science 314 (5799), 626–630.Google Scholar
Huang, R., Chavez, I., Taute, K. M., Luki, B., Jeney, S., Raizen, M. G. & Florin, E. L. 2011 Direct observation of the full transition from ballistic to diffusive brownian motion in a liquid. Nat. Phys. 7 (7), 576–580.Google Scholar
Langevin, P. 1908 Sur la théorie du mouvement brownien. C.R. Acad. Sci. Paris 146, 530–533.Google Scholar
Li, T., Kheifets, S., Medellin, D. & Raizen, M. G. 2010 Measurement of the instantaneous velocity of a brownian particle. Science 328 (5986), 1673–1675.CrossRefGoogle ScholarPubMed
Li, Z. & Wang, H. 2003 Drag force, diffusion coefficient, and electric mobility of small particles. ii. application. Phys. Rev. E 68 (6), 061207.Google Scholar
Li, Z. & Wang, H. 2005 Gas-nanoparticle scattering: a molecular view of momentum accommodation function. Phys. Rev. Lett. 95 (1), 014502.CrossRefGoogle ScholarPubMed
Pusey, P. N. 2011 Brownian motion goes ballistic. Science 332 (6031), 802–803.Google Scholar
Saffman, P. G. & Delbrück, M. 1975 Brownian motion in biological membranes. Proc. Natl Acad. Sci. 72 (8), 3111–3113.CrossRefGoogle ScholarPubMed
Thompson, J. R. & Wilson, J. R. 2016 Multifractal detrended fluctuation analysis: practical applications to financial time series. Math. Comput. Simul. 126, 63–88.Google Scholar
Tobias, D. J., Martyna, G. J. & Klein, M. L. 1993 Molecular dynamics simulations of a protein in the canonical ensemble. J. Phys. Chem. 5, 113–133.Google Scholar
Vorholz, J., Harismiadis, V. I., Rumpf, B., Panagiotopoulos, A. Z. & Maurer, G. 2000 Vapor + liquid equilibrium of water, carbon dioxide, and the binary system, water + carbon dioxide, from molecular simulation. Fluid Phase Equilib. 170 (2), 203–234.Google Scholar