Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ge, Jin
Zhang, Xin-ting
Li, Hai-feng
and
Tian, Bao-lin
2020.
Late-time turbulent mixing induced by multimode Richtmyer–Meshkov instability in cylindrical geometry.
Physics of Fluids,
Vol. 32,
Issue. 12,
Fu, Yaowei
Yu, Changping
and
Li, Xinliang
2020.
Energy transport characteristics of converging Richtmyer–Meshkov instability.
AIP Advances,
Vol. 10,
Issue. 10,
Wang, Dandan
and
Dong, Gang
2020.
Scalar characterisations of three-dimensional shock-flame interactions: similarity and inhomogeneity.
Journal of Turbulence,
Vol. 21,
Issue. 2,
p.
84.
Wang, Dandan
and
Dong, Gang
2020.
Three-dimensional inert and reactive shock-interface interactions: statistical flow characterisations.
Journal of Turbulence,
Vol. 21,
Issue. 4,
p.
209.
Li, Ming
Ding, Juchun
Zhai, Zhigang
Si, Ting
Liu, Naian
Huang, Shenghong
and
Luo, Xisheng
2020.
On divergent Richtmyer–Meshkov instability of a light/heavy interface.
Journal of Fluid Mechanics,
Vol. 901,
Issue. ,
Zhou, Ye
Groom, Michael
and
Thornber, Ben
2020.
Dependence of Enstrophy Transport and Mixed Mass on Dimensionality and Initial Conditions in the Richtmyer–Meshkov Instability Induced Flows1.
Journal of Fluids Engineering,
Vol. 142,
Issue. 12,
Xue, Kun
Shi, Xiaoliang
Zeng, Junsheng
Tian, Baolin
Han, Panpan
Li, Jiarui
Liu, Lan
Meng, Baoqing
Guo, Xiaohu
and
Bai, Chunhua
2020.
Explosion-driven interfacial instabilities of granular media.
Physics of Fluids,
Vol. 32,
Issue. 8,
Peng, Naifu
Yang, Yue
and
Xiao, Zuoli
2021.
Effects of the secondary baroclinic vorticity on the energy cascade in the Richtmyer–Meshkov instability.
Journal of Fluid Mechanics,
Vol. 925,
Issue. ,
Li, Xinliang
Fu, Yaowei
Yu, Changping
and
Li, Li
2021.
Statistical characteristics of turbulent mixing in spherical and cylindrical converging Richtmyer–Meshkov instabilities.
Journal of Fluid Mechanics,
Vol. 928,
Issue. ,
Brasseur, Mathieu
Vandenboomgaerde, Marc
Mariani, Christian
Barros, Diogo C.
Souffland, Denis
and
Jourdan, Georges
2021.
Experimental generation of spherical converging shock waves.
Experiments in Fluids,
Vol. 62,
Issue. 7,
Tang, Jinggang
Zhang, Fu
Luo, Xisheng
and
Zhai, Zhigang
2021.
Effect of Atwood number on convergent Richtmyer–Meshkov instability.
Acta Mechanica Sinica,
Vol. 37,
Issue. 3,
p.
434.
Duval, W. M. B.
Zhong, H.
and
Batur, C.
2021.
Mixing driven by transient buoyancy flows.II. Flow dynamics.
AIP Advances,
Vol. 11,
Issue. 8,
Zhang, Dejia
Xu, Aiguo
Zhang, Yudong
Gan, Yanbiao
and
Li, Yingjun
2022.
Discrete Boltzmann modeling of high-speed compressible flows with various depths of non-equilibrium.
Physics of Fluids,
Vol. 34,
Issue. 8,
Ge, Jin
Li, Haifeng
Zhang, Xinting
and
Tian, Baolin
2022.
Evaluating the stretching/compression effect of Richtmyer–Meshkov instability in convergent geometries.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Zheng, Chun
He, Yong
Zhang, Huanhao
and
Chen, Zhihua
2022.
Effects of the parameters of inner air cylinder on evolution of annular SF6 cylinder accelerated by a planar shock wave.
Physics of Fluids,
Vol. 34,
Issue. 12,
Guo, Wenxuan
and
Zhang, Qiang
2022.
Quantitative theory for spikes and bubbles in the Richtmyer−Meshkov instability at arbitrary density ratios in three dimensions.
Physics of Fluids,
Vol. 34,
Issue. 7,
Li, Jiarui
Xue, Kun
Zeng, Junsheng
Tian, Baolin
and
Guo, Xiaohu
2022.
Shock-induced interfacial instabilities of granular media.
Journal of Fluid Mechanics,
Vol. 930,
Issue. ,
Pei, Lei
Ma, Zongqiang
Zhang, Yang
Shi, Xiaofeng
Ma, Dongjun
Pan, Hao
and
Wang, Pei
2022.
Discrete element simulations on the damaged surface hydrodynamics of tungsten powders with inert Ar gas.
Journal of Applied Physics,
Vol. 131,
Issue. 2,
Shan, Yiming
Xu, Aiguo
Wang, Lifeng
and
Zhang, Yudong
2023.
Nonequilibrium kinetics effects in Richtmyer–Meshkov instability and reshock processes.
Communications in Theoretical Physics,
Vol. 75,
Issue. 11,
p.
115601.
Zhang, Dejia
Xu, Aiguo
Song, Jiahui
Gan, Yanbiao
Zhang, Yudong
and
Li, Yingjun
2023.
Specific-heat ratio effects on the interaction between shock wave and heavy-cylindrical bubble: Based on discrete Boltzmann method.
Computers & Fluids,
Vol. 265,
Issue. ,
p.
106021.
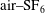 $\text{air}{-}\text{SF}_{6}$ interfaces with different amplitudes and wavelengths are considered. For all cases, the perturbation amplitude experiences a linear growth much longer than that in the planar geometry. A compressible linear model is derived by considering a constant uniform fluid compression, which shows a slight difference to the incompressible theory. However, both the linear models overestimate the perturbation growth from a very early stage due to the presence of strong nonlinearity. The nonlinear model of Wang et al. (Phys. Plasmas, vol. 22, 2015, 082702) is demonstrated to predict well the amplitude growth up to a normalized time of 1.0. The prolongation of the linear increment is mainly ascribed to the counteraction between the promotion by geometric convergence and the suppression by nonlinearity. Growths of the first three harmonics, obtained by a Fourier analysis of the interface contour, provide a first thorough validation of the nonlinear theory.
$\text{air}{-}\text{SF}_{6}$ interfaces with different amplitudes and wavelengths are considered. For all cases, the perturbation amplitude experiences a linear growth much longer than that in the planar geometry. A compressible linear model is derived by considering a constant uniform fluid compression, which shows a slight difference to the incompressible theory. However, both the linear models overestimate the perturbation growth from a very early stage due to the presence of strong nonlinearity. The nonlinear model of Wang et al. (Phys. Plasmas, vol. 22, 2015, 082702) is demonstrated to predict well the amplitude growth up to a normalized time of 1.0. The prolongation of the linear increment is mainly ascribed to the counteraction between the promotion by geometric convergence and the suppression by nonlinearity. Growths of the first three harmonics, obtained by a Fourier analysis of the interface contour, provide a first thorough validation of the nonlinear theory.



