Article contents
Liquid plug formation from heated binary mixtures in capillary tubes
Published online by Cambridge University Press: 24 February 2020
Abstract
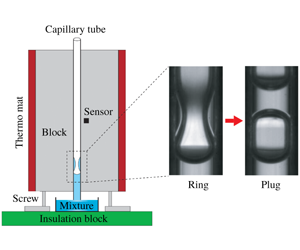
We study the formation of liquid plugs in a vertical heated tube in contact with a reservoir filled with a binary liquid mixture. Various morphologies, such as liquid films, rings and plugs, are observed. A key phenomenon is the transition between a liquid ring and a plug, which is described using the concept of a quasi-static minimal energy surface that becomes unstable when the liquid volume exceeds a specific value. The critical diameter of the liquid ring and the volume and the position of the formed plug are obtained from an analytical model. The inner diameter of the liquid ring obeys a  $d_{l}\sim (t_{0}-t)^{0.57\pm 0.02}$ scaling law shortly before forming a plug at time
$d_{l}\sim (t_{0}-t)^{0.57\pm 0.02}$ scaling law shortly before forming a plug at time  $t_{0}$. The height of the liquid column created develops according to
$t_{0}$. The height of the liquid column created develops according to  $X\sim (t-t_{0})^{0.5\pm 0.01}$ in the first moments. The subsequent time evolution is described by a damped harmonic oscillator based on a scaling analysis. The discoveries presented in this work could be of great importance for our understanding of thermally induced interfacial phenomena in confined space.
$X\sim (t-t_{0})^{0.5\pm 0.01}$ in the first moments. The subsequent time evolution is described by a damped harmonic oscillator based on a scaling analysis. The discoveries presented in this work could be of great importance for our understanding of thermally induced interfacial phenomena in confined space.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 5
- Cited by




