Article contents
Linear stability of magnetohydrodynamic flow in a perfectly conducting rectangular duct
Published online by Cambridge University Press: 10 August 2012
Abstract
We analyse numerically the linear stability of a liquid-metal flow in a rectangular duct with perfectly electrically conducting walls subject to a uniform transverse magnetic field. A non-standard three-dimensional vector stream-function/vorticity formulation is used with a Chebyshev collocation method to solve the eigenvalue problem for small-amplitude perturbations. A relatively weak magnetic field is found to render the flow linearly unstable as two weak jets appear close to the centre of the duct at the Hartmann number 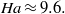 In a sufficiently strong magnetic field, the instability following the jets becomes confined in the layers of characteristic thickness
In a sufficiently strong magnetic field, the instability following the jets becomes confined in the layers of characteristic thickness 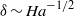 located at the walls parallel to the magnetic field. In this case the instability is determined by
located at the walls parallel to the magnetic field. In this case the instability is determined by 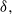 which results in both the critical Reynolds number and wavenumber scaling as
which results in both the critical Reynolds number and wavenumber scaling as 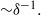 Instability modes can have one of the four different symmetry combinations along and across the magnetic field. The most unstable is a pair of modes with an even distribution of vorticity along the magnetic field. These two modes represent strongly non-uniform vortices aligned with the magnetic field, which rotate either in the same or opposite senses across the magnetic field. The former enhance while the latter weaken one another provided that the magnetic field is not too strong or the walls parallel to the field are not too far apart. In a strong magnetic field, when the vortices at the opposite walls are well separated by the core flow, the critical Reynolds number and wavenumber for both of these instability modes are the same:
Instability modes can have one of the four different symmetry combinations along and across the magnetic field. The most unstable is a pair of modes with an even distribution of vorticity along the magnetic field. These two modes represent strongly non-uniform vortices aligned with the magnetic field, which rotate either in the same or opposite senses across the magnetic field. The former enhance while the latter weaken one another provided that the magnetic field is not too strong or the walls parallel to the field are not too far apart. In a strong magnetic field, when the vortices at the opposite walls are well separated by the core flow, the critical Reynolds number and wavenumber for both of these instability modes are the same: 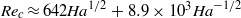 and
and 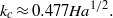 The other pair of modes, which differs from the previous one by an odd distribution of vorticity along the magnetic field, is more stable with an approximately four times higher critical Reynolds number.
The other pair of modes, which differs from the previous one by an odd distribution of vorticity along the magnetic field, is more stable with an approximately four times higher critical Reynolds number.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 18
- Cited by




