Article contents
Improved scaling laws for the shock-induced dispersal of a dense particle curtain
Published online by Cambridge University Press: 08 August 2019
Abstract
Experiments were performed within Sandia National Labs’ Multiphase Shock Tube to measure and quantify the shock-induced dispersal of a shock/dense particle curtain interaction. Following interaction with a planar travelling shock wave, schlieren imaging at 75 kHz was used to track the upstream and downstream edges of the curtain. Data were obtained for two particle diameter ranges (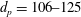 $d_{p}=106{-}125$,
$d_{p}=106{-}125$, 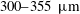 $300{-}355~\unicode[STIX]{x03BC}\text{m}$) across Mach numbers ranging from 1.24 to 2.02. Using these data, along with data compiled from the literature, the dispersion of a dense curtain was studied for multiple Mach numbers (1.2–2.6), particle sizes (
$300{-}355~\unicode[STIX]{x03BC}\text{m}$) across Mach numbers ranging from 1.24 to 2.02. Using these data, along with data compiled from the literature, the dispersion of a dense curtain was studied for multiple Mach numbers (1.2–2.6), particle sizes (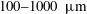 $100{-}1000~\unicode[STIX]{x03BC}\text{m}$) and volume fractions (9–32 %). Data were non-dimensionalized according to two different scaling methods found within the literature, with time scales defined based on either particle propagation time or pressure ratio across a reflected shock. The data show that spreading of the particle curtain is a function of the volume fraction, with the effectiveness of each time scale based on the proximity of a given curtain’s volume fraction to the dilute mixture regime. It is seen that volume fraction corrections applied to a traditional particle propagation time scale result in the best collapse of the data between the two time scales tested here. In addition, a constant-thickness regime has been identified, which has not been noted within previous literature.
$100{-}1000~\unicode[STIX]{x03BC}\text{m}$) and volume fractions (9–32 %). Data were non-dimensionalized according to two different scaling methods found within the literature, with time scales defined based on either particle propagation time or pressure ratio across a reflected shock. The data show that spreading of the particle curtain is a function of the volume fraction, with the effectiveness of each time scale based on the proximity of a given curtain’s volume fraction to the dilute mixture regime. It is seen that volume fraction corrections applied to a traditional particle propagation time scale result in the best collapse of the data between the two time scales tested here. In addition, a constant-thickness regime has been identified, which has not been noted within previous literature.
- Type
- JFM Papers
- Information
- Creative Commons
- This is a work of the U.S. Government and is not subject to copyright protection in the United States.
- Copyright
- © 2019 Cambridge University Press
References
- 19
- Cited by




