Article contents
Gyrotactic trapping of micro-swimmers in simple shear flows: a study directly from the fundamental Smoluchowski equation
Published online by Cambridge University Press: 31 March 2022
Abstract
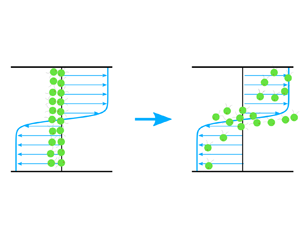
Thin phytoplankton layers with vertically compressed structures found in stratified lakes and coastal water bodies have been a hot-spot in marine science and fluid mechanics. Although extensive efforts have been made to explore gyrotactic trapping as a possible mechanism, obvious inconsistencies remain there between the generalised Taylor dispersion method and individual-based model. In this work, a study directly from the fundamental Smoluchowski equation is carried out on the gyrotactic trapping mechanism in representative simple shear flows. With no approximation made to the fundamental equation and applying a biorthogonal expansion to the local moments of the probability density function, the evolution and steady state of the transport process are in good agreement with results of individual-based model, thus removing the gap between the continuum approach and individual-based model. The influences of strongly varying shear rate and boundary effect are reasonably scrutinised. The average swimming orientation with fixed local shear is highlighted as time-dependent rather than steady as previously assumed. The variations of characteristic time of the transient thin layer as functions of the flow intensity, gyrotaxis intensity and swimming ability are characterised. Sedimentation of the micro-swimmers is considered in some cases to reflect that micro-organisms are possibly negatively buoyant, with corresponding boundary conditions devised. A steady thin layer can be realised in the solution by adding a small settling speed to counteract the gravitactic focusing at the upper surface.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 10
- Cited by





