Article contents
Fluid invasion of an unsaturated leaky porous layer
Published online by Cambridge University Press: 21 July 2015
Abstract
We study the flow and leakage of gravity currents injected into an unsaturated (dry), vertically confined porous layer containing a localized outlet or leakage point in its lower boundary. The leakage is driven by the combination of the gravitational hydrostatic pressure head of the current above the outlet and the pressure build-up from driving fluid downstream of the leakage point. Model solutions illustrate transitions towards one of three long-term regimes of flow, depending on the value of a dimensionless parameter 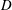 $D$, which, when positive, represents the ratio of the hydrostatic head above the outlet for which gravity-driven leakage balances the input flux, to the depth of the medium. If
$D$, which, when positive, represents the ratio of the hydrostatic head above the outlet for which gravity-driven leakage balances the input flux, to the depth of the medium. If 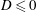 $D\leqslant 0$, the input flux is insufficient to accumulate any fluid above the outlet and fluid migrates directly through the leakage pathway. If
$D\leqslant 0$, the input flux is insufficient to accumulate any fluid above the outlet and fluid migrates directly through the leakage pathway. If 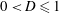 $0<D\leqslant 1$, some fluid propagates downstream of the outlet but retains a free surface above it. The leakage rate subsequently approaches the input flux asymptotically but much more gradually than if
$0<D\leqslant 1$, some fluid propagates downstream of the outlet but retains a free surface above it. The leakage rate subsequently approaches the input flux asymptotically but much more gradually than if 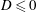 $D\leqslant 0$. If
$D\leqslant 0$. If 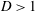 $D>1$, the current fills the entire depth of the medium above the outlet. Confinement then fixes gravity-driven leakage at a constant rate but introduces a new force driving leakage in the form of the pressure build-up associated with mobilizing fluid downstream of the outlet. This causes the leakage rate to approach the injection rate faster than would occur in the absence of the confining boundary. This conclusion is in complete contrast to fluid-saturated media, where confinement can potentially reduce long-term leakage by orders of magnitude. Data from a new series of laboratory experiments confirm these predictions.
$D>1$, the current fills the entire depth of the medium above the outlet. Confinement then fixes gravity-driven leakage at a constant rate but introduces a new force driving leakage in the form of the pressure build-up associated with mobilizing fluid downstream of the outlet. This causes the leakage rate to approach the injection rate faster than would occur in the absence of the confining boundary. This conclusion is in complete contrast to fluid-saturated media, where confinement can potentially reduce long-term leakage by orders of magnitude. Data from a new series of laboratory experiments confirm these predictions.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 2
- Cited by





