Article contents
Flow regimes for a square cross-section cylinder in oscillatory flow
Published online by Cambridge University Press: 17 January 2017
Abstract
Two-dimensional direct numerical simulation and Floquet stability analysis have been performed at moderate Keulegan–Carpenter number (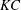 $KC$) and low Reynolds number (
$KC$) and low Reynolds number (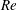 $Re$) for a square cross-section cylinder with its face normal to the oscillatory flow. Based on the numerical simulations a map of flow regimes is formed and compared to the map of flow around an oscillating circular cylinder by Tatsuno & Bearman (J. Fluid Mech., vol. 211, 1990, pp. 157–182). Two new flow regimes have been observed, namely A
$Re$) for a square cross-section cylinder with its face normal to the oscillatory flow. Based on the numerical simulations a map of flow regimes is formed and compared to the map of flow around an oscillating circular cylinder by Tatsuno & Bearman (J. Fluid Mech., vol. 211, 1990, pp. 157–182). Two new flow regimes have been observed, namely A $^{\prime }$ and F
$^{\prime }$ and F $^{\prime }$. The regime A
$^{\prime }$. The regime A $^{\prime }$ found at low
$^{\prime }$ found at low 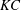 $KC$ is characterised by the transverse convection of fluid particles perpendicular to the motion; and the regime F
$KC$ is characterised by the transverse convection of fluid particles perpendicular to the motion; and the regime F $^{\prime }$ found at high
$^{\prime }$ found at high 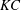 $KC$ shows a quasi-periodic feature with a well-defined secondary period, which is larger than the oscillation period. The Floquet analysis demonstrates that when the two-dimensional flow breaks the reflection symmetry about the axis of oscillation, the quasi-periodic instability and the synchronous instability with the imposed oscillation occur alternately for the square cylinder along the curve of marginal stability. This alternate pattern in instabilities leads to four distinct flow regimes. When compared to the vortex shedding in otherwise unidirectional flow, the two quasi-periodic flow regimes are observed when the oscillation frequency is close to the Strouhal frequency (or to half of it). Both the flow regimes and marginal stability curve shift in the
$KC$ shows a quasi-periodic feature with a well-defined secondary period, which is larger than the oscillation period. The Floquet analysis demonstrates that when the two-dimensional flow breaks the reflection symmetry about the axis of oscillation, the quasi-periodic instability and the synchronous instability with the imposed oscillation occur alternately for the square cylinder along the curve of marginal stability. This alternate pattern in instabilities leads to four distinct flow regimes. When compared to the vortex shedding in otherwise unidirectional flow, the two quasi-periodic flow regimes are observed when the oscillation frequency is close to the Strouhal frequency (or to half of it). Both the flow regimes and marginal stability curve shift in the 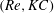 $(Re,KC)$-space compared to the oscillatory flow around a circular cylinder and this shift appears to be consistent with the change in vortex formation time associated with the lower Strouhal frequency of the square cylinder.
$(Re,KC)$-space compared to the oscillatory flow around a circular cylinder and this shift appears to be consistent with the change in vortex formation time associated with the lower Strouhal frequency of the square cylinder.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 15
- Cited by



