Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-17T10:54:32.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of poles in two-dimensional hydrodynamics with free surface: new constants of motion

Published online by Cambridge University Press:  12 July 2019

A. I. Dyachenko Open the ORCID record for A. I. Dyachenko [Opens in a new window] ,
S. A. Dyachenko Open the ORCID record for S. A. Dyachenko [Opens in a new window] ,
P. M. Lushnikov Open the ORCID record for P. M. Lushnikov [Opens in a new window]  and
V. E. Zakharov
A. I. Dyachenko
Affiliation:
Landau Institute for Theoretical Physics, Chernogolovka, 142432, Russia Center for Advanced Studies, Skoltech, Moscow, 143026, Russia
S. A. Dyachenko
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA Department of Applied Mathematics, University of Washington, Seattle, WA 98195, USA
P. M. Lushnikov*
Affiliation:
Landau Institute for Theoretical Physics, Chernogolovka, 142432, Russia Department of Mathematics and Statistics, University of New Mexico, Albuquerque, NM 87131, USA
V. E. Zakharov
Affiliation:
Landau Institute for Theoretical Physics, Chernogolovka, 142432, Russia Center for Advanced Studies, Skoltech, Moscow, 143026, Russia Department of Mathematics, University of Arizona, Tucson, AZ 85721, USA
*
†Email address for correspondence: plushnik@math.unm.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We address the problem of the potential motion of an ideal incompressible fluid with a free surface and infinite depth in a two-dimensional geometry. We admit the presence of gravity forces and surface tension. A time-dependent conformal mapping 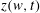$z(w,t)$ of the lower complex half-plane of the variable 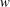$w$ into the area filled with fluid is performed with the real line of 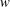$w$ mapped into the free fluid’s surface. We study the dynamics of singularities of both 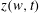$z(w,t)$ and the complex fluid potential 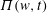$\unicode[STIX]{x1D6F1}(w,t)$ in the upper complex half-plane of 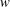$w$. 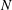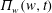We show the existence of solutions with an arbitrary finite number $N$ of complex poles in $z_{w}(w,t)$ and $\unicode[STIX]{x1D6F1}_{w}(w,t)$ which are the derivatives of 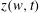$z(w,t)$ and 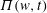$\unicode[STIX]{x1D6F1}(w,t)$ over 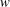$w$. We stress that these solutions are not purely rational because they generally have branch points at other positions of the upper complex half-plane. The orders of poles can be arbitrary for zero surface tension while all orders are even for non-zero surface tension. We find that the residues of 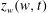$z_{w}(w,t)$ at these 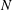$N$ points are new, previously unknown, constants of motion, see also Zakharov & Dyachenko (2012, authors’ unpublished observations, arXiv:1206.2046) for the preliminary results. All these constants of motion commute with each other in the sense of the underlying Hamiltonian dynamics. In the absence of both gravity and surface tension, the residues of 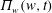$\unicode[STIX]{x1D6F1}_{w}(w,t)$ are also the constants of motion while non-zero gravity 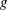$g$ ensures a trivial linear dependence of these residues on time. A Laurent series expansion of both 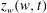$z_{w}(w,t)$ and 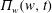$\unicode[STIX]{x1D6F1}_{w}(w,t)$ at each poles position reveals the existence of additional integrals of motion for poles of the second order. If all poles are simple then the number of independent real integrals of motion is 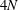$4N$ for zero gravity and 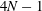$4N-1$ for non-zero gravity. For the second-order poles we found 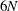$6N$ motion integrals for zero gravity and 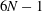$6N-1$ for non-zero gravity. We suggest that the existence of these non-trivial constants of motion provides an argument in support of the conjecture of complete integrability of free surface hydrodynamics in deep water. Analytical results are solidly supported by high precision numerics.

JFM classification

Mathematical Foundations: General fluid mechanics Mathematical Foundations: Hamiltonian theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 891 - 925
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alpert, B., Greengard, L. & Hagstrom, T. 2000 Rapid evaluation of nonreflecting boundary kernels for time-domain wave propagation. SIAM J. Numer. Anal. 37, 1138–1164.10.1137/S0036142998336916Google Scholar
Arnold, V. I. 1989 Mathematical Methods of Classical Mechanics. Springer.10.1007/978-1-4757-2063-1Google Scholar
Baker, G., Caflisch, R. E. & Siegel, M. 1993 Singularity formation during Rayleigh–Taylor instability. J. Fluid Mech. 252, 51–78.10.1017/S0022112093003660Google Scholar
Baker, G. R., Meiron, D. I. & Orszag, S. A. 1982 Generalized vortex methods for free-surface flow problems. J. Fluid Mech. 123, 477–501.10.1017/S0022112082003164Google Scholar
Baker, G. R. & Shelley, M. J. 1990 On the connection between thin vortex layers and vortex sheets. J. Fluid Mech. 215, 161–194.10.1017/S0022112090002609Google Scholar
Baker, G. R. & Xie, C. 2011 Singularities in the complex physical plane for deep water waves. J. Fluid Mech. 685, 83–116.Google Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods: Second Revised Edition. Dover Publications.Google Scholar
Caflisch, R. & Orellana, O. 1989 Singular solutions and ill–posedness for the evolution of vortex sheets. SIAM J. Math. Anal. 20 (2), 293–307.Google Scholar
Caflisch, R., Orellana, O. & Siegel, M. 1990 A localized approximation method for vortical flows. SIAM J. Appl. Maths 50 (6), 1517–1532.Google Scholar
Caflisch, R. E., Ercolani, N., Hou, T. Y. & Landis, Y. 1993 Multi-valued solutions and branch point singularities for nonlinear hyperbolic or elliptic systems. Commun. Pure Appl. Maths 46 (4), 453–499.10.1002/cpa.3160460402Google Scholar
Chalikov, D. & Sheinin, D. 1998 Direct modeling of one-dimensional nonlinear potential waves. Adv. Fluid Mech. 17, 207–258.Google Scholar
Chalikov, D. & Sheinin, D. 2005 Modeling of extreme waves based on equation of potential flow with a free surface. J. Comput. Phys. 210, 247–273.Google Scholar
Chalikov, D. V. 2016 Numerical Modeling of Sea Waves. Springer.10.1007/978-3-319-32916-1Google Scholar
Cowley, S. J., Baker, G. R. & Tanveer, S. 1999 On the formation of Moore curvature singularities in vortex sheets. J. Fluid Mech. 378, 233–267.10.1017/S0022112098003334Google Scholar
Crowdy, D. G. 2002 On a class of geometry-driven free boundary problems. SIAM. J. Appl. Maths 62, 945–954.Google Scholar
Dubrovin, B. A., Fomenko, A. T. & Novikov, S. P. 1985 Modern Geometry: Methods and Applications: Part II: The Geometry and Topology of Manifolds. Springer.Google Scholar
Dyachenko, A. I. 2001 On the dynamics of an ideal fluid with a free surface. Dokl. Math. 63 (1), 115–117.Google Scholar
Dyachenko, A. I., Kachulin, D. I. & Zakharov, V. E. 2013a On the nonintegrability of the free surface hydrodynamics. JETP Lett. 98, 43–47.Google Scholar
Dyachenko, A. I., Kuznetsov, E. A., Spector, M. & Zakharov, V. E. 1996 Analytical description of the free surface dynamics of an ideal fluid (canonical formalism and conformal mapping). Phys. Lett. A 221, 73–79.10.1016/0375-9601(96)00417-3Google Scholar
Dyachenko, A. I., Lushnikov, P. M. & Zakharov, V. E. 2019 Non-canonical Hamiltonian structure and Poisson bracket for two-dimensional hydrodynamics with free surface. J. Fluid Mech. 869, 526–552.10.1017/jfm.2019.219Google Scholar
Dyachenko, A. I. & Zakharov, V. E. 1994 Is free surface hydrodynamics an integrable system? Phys. Lett. A 190 (2), 144–148.Google Scholar
Dyachenko, S. & Newell, A. C. 2016 Whitecapping. Stud. Appl. Maths 137, 199–213.Google Scholar
Dyachenko, S. A., Lushnikov, P. M. & Korotkevich, A. O. 2013b The complex singularity of a Stokes wave. JETP Lett. 98 (11), 675–679.Google Scholar
Dyachenko, S. A., Lushnikov, P. M. & Korotkevich, A. O. 2016 Branch cuts of Stokes wave on deep water. Part I. Numerical solution and Padé approximation. Stud. Appl. Maths 137, 419–472.10.1111/sapm.12128Google Scholar
Baker, G. A. Jr & Graves-Morris, P. R. 1996 Padé Approximants, 2nd edn. Cambridge University Press.Google Scholar
Gardner, C. S., Greene, J. M., Kruskal, M. D. & Miura, R. M. 1967 Method for solving the Korteweg-deVries equation. Phys. Rev. Lett. 19, 1095–1097.Google Scholar
Gonnet, P., Pachon, R. & Trefethen, L. N. 2011 Robust rational interpolation and least-squares. Elec. Trans. Numer. Anal. 1388, 146–167.Google Scholar
Grant, M. A. 1973 The singularity at the crest of a finite amplitude progressive Stokes wave. J. Fluid Mech. 59 (2), 257–262.Google Scholar
Karabut, E. A. & Zhuravleva, E. N. 2014 Unsteady flows with a zero acceleration on the free boundary. J. Fluid Mech. 754, 308–331.10.1017/jfm.2014.401Google Scholar
Krasny, R. 1986 A study of singularity formation in a vortex sheet by the point–vortex approximation. J. Fluid Mech. 167, 65–93.10.1017/S0022112086002732Google Scholar
Kuznetsov, E. A., Spector, M. D. & Zakharov, V. E. 1993 Surface singularities of ideal fluid. Phys. Lett. A 182 (4–6), 387–393.Google Scholar
Kuznetsov, E. A., Spector, M. D. & Zakharov, V. E. 1994 Formation of singularities on the free surface of an ideal fluid. Phys. Rev. E 49, 1283–1290.10.1103/PhysRevE.49.1283Google Scholar
Lamb, H. 1945 Hydrodynamics. Dover Books on Physics.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1989 Fluid Mechanics, 3rd edn. vol. 6. Pergamon.Google Scholar
Lushnikov, P. M. & Zubarev, N. M. 2018 Exact solutions for nonlinear development of a Kelvin–Helmholtz instability for the counterflow of superfluid and normal components of Helium II. Phys. Rev. Lett. 120, 204504.10.1103/PhysRevLett.120.204504Google Scholar
Lushnikov, P. M. 2004 Exactly integrable dynamics of interface between ideal fluid and light viscous fluid. Phys. Lett. A 329, 49–54.Google Scholar
Lushnikov, P. M. 2016 Structure and location of branch point singularities for Stokes waves on deep water. J. Fluid Mech. 800, 557–594.10.1017/jfm.2016.405Google Scholar
Lushnikov, P. M., Dyachenko, S. A. & Silantyev, D. A. 2017 New conformal mapping for adaptive resolving of the complex singularities of Stokes wave. Proc. R. Soc. Lond. A 473, 20170198.Google Scholar
Meiron, D. I., Baker, G. R. & Orszag, S. A. 1982 Analytic structure of vortex sheet dynamics. Part 1. Kelvin–Helmholtz instability. J. Fluid Mech. 114, 283–298.Google Scholar
Meison, D., Orzag, S. & Izraely, M. 1981 Applications of numerical conformal mapping. J. Comput. Phys. 40, 345–360.Google Scholar
Mineev-Weinstein, M., Wiegmann, P. B. & Zabrodin, A. 2000 Integrable structure of interface dynamics. Phys. Rev. Lett. 84 (22), 5106–5109.Google Scholar
Moore, D. W. 1979 The spontaneous appearance of a singularity in the shape of an evolving vortex sheet. Proc. R. Soc. Lond. A 365 (1720), 105–119.Google Scholar
Novikov, S., Manakov, S. V., Pitaevskii, L. P. & Zakharov, V. E. 1984 Theory of Solitons: The Inverse Scattering Method. Springer.Google Scholar
Ovsyannikov, L. V. 1973 Dynamics of a fluid. M.A. Lavrent’ev Institute of Hydrodynamics Sib. Branch USSR Ac. Sci. 15, 104–125.Google Scholar
Richardson, S. 1972 Hele Shaw flows with a free boundary produced by the injection of fluid into a narrow channel. J. Fluid Mech. 56, 609–618.Google Scholar
Shelley, M. J. 1992 A study of singularity formation in vortex–sheet motion by a spectrally accurate vortex method. J. Fluid Mech. 244, 493–526.Google Scholar
Stokes, G. G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–455.Google Scholar
Stokes, G. G. 1880 On the theory of oscillatory waves. Math. Phys. Papers 1, 197–229.Google Scholar
Tanveer, S. 1991 Singularities in water waves and Rayleigh–Taylor instability. Proc. R. Soc. Lond. A 435, 137–158.Google Scholar
Tanveer, S. 1993 Singularities in the classical Rayleigh–Taylor flow: formation and subsequent motion. Proc. R. Soc. Lond. A 441, 501–525.Google Scholar
Weinstein, A. 1983 The local structure of Poisson manifolds. J. Differ. Geom. 18, 523–557.10.4310/jdg/1214437787Google Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on a surface. J. Appl. Mech. Tech. Phys. 9 (2), 190–194.Google Scholar
Zakharov, V. E. & Dyachenko, A. I.2012 Free-surface hydrodynamics in the conformal variables, authors’ unpublished observations, arXiv:1206.2046.Google Scholar
Zakharov, V. E., Dyachenko, A. I. & Vasiliev, O. A. 2002 New method for numerical simulation of nonstationary potential flow of incompressible fluid with a free surface. Eur. J. Mech. (B/Fluids) 21, 283–291.10.1016/S0997-7546(02)01189-5Google Scholar
Zakharov, V. E. & Faddeev, L. D. 1971 Korteweg-de Vries equation: A completely integrable Hamiltonian system. Funct. Anal. Applics 5, 280–287.Google Scholar
Zakharov, V. E. & Shabat, A. B. 1972 Exact theory of 2-dimensional sef-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 34, 62.Google Scholar
Zubarev, N. M. 2000 Charged-surface instability development in liquid helium: an exact solution. JETP Lett. 71, 367–369.Google Scholar
Zubarev, N. M. 2002 Exact solutions of the equations of motion of liquid helium with a charged free surface. J. Expl Theor. Phys. 94, 534–544.10.1134/1.1469153Google Scholar
Zubarev, N. M. 2008 Formation of singularities on the charged surface of a liquid-helium layer with a finite depth. J. Expl Theor. Phys. 107, 668–678.Google Scholar
Zubarev, N. M. & Karabut, E. A. 2018 Exact local solutions for the formation of singularities on the free surface of an ideal fluid. JETP Lett. 107, 412–417.10.1134/S0021364018070135Google Scholar
Zubarev, N. M. & Kuznetsov, E. A. 2014 Singularity formation on a fluid interface during the Kelvin–Helmholtz instability development. J. Expl Theor. Phys. 119, 169–178.10.1134/S1063776114060077Google Scholar