Article contents
Drag force in granular shear flows: regimes, scaling laws and implications for segregation
Published online by Cambridge University Press: 08 September 2022
Abstract
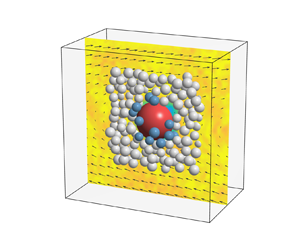
The drag force on a spherical intruder in dense granular shear flows is studied using discrete element method simulations. Three regimes of the intruder dynamics are observed depending on the magnitude of the drag force (or the corresponding intruder velocity) and the flow inertial number: a fluctuation-dominated regime for small drag forces; a viscous regime for intermediate drag forces; and an inertial (cavity formation) regime for large drag forces. The transition from the viscous regime (linear force-velocity relation) to the inertial regime (quadratic force-velocity relation) depends further on the inertial number. Despite these distinct intruder dynamics, we find a quantitative similarity between the intruder drag in granular shear flows and the Stokesian drag on a sphere in a viscous fluid for intruder Reynolds numbers spanning five orders of magnitude. Beyond this first-order description, a modified Stokes drag model is developed that accounts for the secondary dependence of the drag coefficient on the inertial number and the intruder size and density ratios. When the drag model is coupled with a segregation force model for intruders in dense granular flows, it is possible to predict the velocity of gravity-driven segregation of an intruder particle in shear flow simulations.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
Footnotes
Present address: Institute for Ocean Engineering, Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, PR China.
References
REFERENCES
Jing et al. Supplementary Movie 1
Vertical position of an intruder particle vs. time (left panel) and the corresponding animation (right panel) showing the intruder (red) and its contacting (blue) and non-contacting (grey) neighboring bed particles in an annular region around the intruder. The intruder has the same size and density as the bed particles ($R=1$ and $R_\rho=1$). The flow conditions are $P_0=1000\ \textrm{Pa}$ and $\dot\gamma_0=10\ \textrm{s}^{-1}$ ($I=0.08$), and the drag force (or, equivalently, the external driving force) is $F_d/P_0d_i^2=0.05$. Note the significant fluctuations and intermittency of the intruder position due to particle collisions at this small driving force.
- 3
- Cited by





