Article contents
Direct numerical simulation of quasi-two-dimensional MHD turbulent shear flows
Published online by Cambridge University Press: 01 April 2021
Abstract
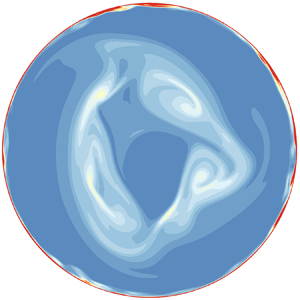
High-resolution direct numerical simulations are performed to study the turbulent shear flow of liquid metal in a cylindrical container. The flow is driven by an azimuthal Lorentz force induced by the interaction between the radial electric currents injected through electrodes placed at the bottom wall and a magnetic field imposed in the axial direction. All physical parameters, are aligned with the experiment by Messadek & Moreau (J. Fluid Mech. vol. 456, 2002, pp. 137–159). The simulations recover the variations of angular momentum, velocity profiles, boundary layer thickness and turbulent spectra found experimentally to a very good precision. They further reveal a transition to small scale turbulence in the wall side layer when the Reynolds number based on Hartmann layer thickness  $R$ exceeds 121, and a separation of this layer for
$R$ exceeds 121, and a separation of this layer for  $R \geq 145.2$. Ekman recirculations significantly influence these quantities and determine global dissipation. This phenomenology well captured by the 2-D PSM model (Pothérat, Sommeria & Moreau, J. Fluid Mech. vol. 424, 2000, pp. 75–100) until small-scale turbulence appears and incurs significant extra dissipation only captured by 3-D simulations. Secondly, we recover the theoretical law for the cutoff scale separating large quasi-two-dimensional (Q2-D) scales from small three-dimensional ones (Sommeria & Moreau, J. Fluid Mech. vol. 118, 1982, pp. 507–518), and thus establish its validity in sheared magnetohydrodynamics (MHD) turbulence. We further find that three-componentality and three-dimensionality appear concurrently and that both the frequency corresponding to the Q2-D cutoff scale and the mean energy associated with he axial component of velocity scale with the true interaction parameter
$R \geq 145.2$. Ekman recirculations significantly influence these quantities and determine global dissipation. This phenomenology well captured by the 2-D PSM model (Pothérat, Sommeria & Moreau, J. Fluid Mech. vol. 424, 2000, pp. 75–100) until small-scale turbulence appears and incurs significant extra dissipation only captured by 3-D simulations. Secondly, we recover the theoretical law for the cutoff scale separating large quasi-two-dimensional (Q2-D) scales from small three-dimensional ones (Sommeria & Moreau, J. Fluid Mech. vol. 118, 1982, pp. 507–518), and thus establish its validity in sheared magnetohydrodynamics (MHD) turbulence. We further find that three-componentality and three-dimensionality appear concurrently and that both the frequency corresponding to the Q2-D cutoff scale and the mean energy associated with he axial component of velocity scale with the true interaction parameter  $N_t$, respectively, as
$N_t$, respectively, as  $0.063 N_t^{0.37}$ and
$0.063 N_t^{0.37}$ and  $0.126N_t^{-0.92}$.
$0.126N_t^{-0.92}$.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 12
- Cited by





