Article contents
Direct numerical simulation of elastic turbulence in the Taylor–Couette flow: transition pathway and mechanistic insight
Published online by Cambridge University Press: 06 October 2022
Abstract
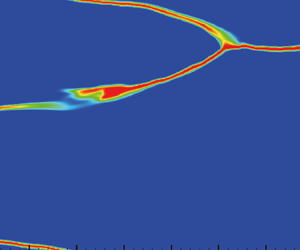
Three-dimensional elastic turbulence in Taylor–Couette flows of dilute polymer solutions has been realized and thoroughly investigated via direct numerical simulations. A novel flow transition pathway from elastically dominated turbulence to solitary vortex pairs (or diwhirls) and eventually to elastic turbulence is observed by decreasing the fluid inertia ( $Re$) over seven orders of magnitude, i.e. from
$Re$) over seven orders of magnitude, i.e. from  $Re=1000$ to
$Re=1000$ to  $0.0001$. The dominant spatio-temporal flow features in the elastic turbulence regime are those of large-scale unsteady diwhirls and small-scale axial and azimuthal travelling waves in the outer and inner halves of the gap, respectively. Moreover, it is conclusively shown that production of turbulent kinetic energy in purely elastic turbulence solely arises due to the stochastic nature of polymer stretch/relaxation. Overall, based on this comprehensive numerical investigation, the differences in the underlying fluid physics that give rise to turbulent fluctuations in elastically dominated and purely elastic turbulence have been delineated.
$0.0001$. The dominant spatio-temporal flow features in the elastic turbulence regime are those of large-scale unsteady diwhirls and small-scale axial and azimuthal travelling waves in the outer and inner halves of the gap, respectively. Moreover, it is conclusively shown that production of turbulent kinetic energy in purely elastic turbulence solely arises due to the stochastic nature of polymer stretch/relaxation. Overall, based on this comprehensive numerical investigation, the differences in the underlying fluid physics that give rise to turbulent fluctuations in elastically dominated and purely elastic turbulence have been delineated.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 9
- Cited by





