Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Jianming
Ding, Juchun
Si, Ting
and
Luo, Xisheng
2020.
Convergent Richtmyer–Meshkov instability of light gas layer with perturbed outer surface.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Sun, Rui
Ding, Juchun
Zhai, Zhigang
Si, Ting
and
Luo, Xisheng
2020.
Convergent Richtmyer–Meshkov instability of heavy gas layer with perturbed inner surface.
Journal of Fluid Mechanics,
Vol. 902,
Issue. ,
Liang, Yu
Liu, Lili
Zhai, Zhigang
Si, Ting
and
Wen, Chih-Yung
2020.
Evolution of shock-accelerated heavy gas layer.
Journal of Fluid Mechanics,
Vol. 886,
Issue. ,
Fu, Yaowei
Yu, Changping
and
Li, Xinliang
2020.
Energy transport characteristics of converging Richtmyer–Meshkov instability.
AIP Advances,
Vol. 10,
Issue. 10,
Pfeiffer, Patricia
Zeng, Qingyun
Tan, Beng Hau
and
Ohl, Claus-Dieter
2020.
Merging of soap bubbles and why surfactant matters.
Applied Physics Letters,
Vol. 116,
Issue. 10,
Li, Xinliang
Fu, Yaowei
Yu, Changping
and
Li, Li
2021.
Statistical characteristics of turbulent mixing in spherical and cylindrical converging Richtmyer–Meshkov instabilities.
Journal of Fluid Mechanics,
Vol. 928,
Issue. ,
Ding, Juchun
Deng, Xiaoming
and
Luo, Xisheng
2021.
Convergent Richtmyer–Meshkov instability on a light gas layer with perturbed inner and outer surfaces.
Physics of Fluids,
Vol. 33,
Issue. 10,
Liang, Yu
and
Luo, Xisheng
2021.
Shock-induced dual-layer evolution.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Feng, Lili
Xu, Jinru
Zhai, Zhigang
and
Luo, Xisheng
2021.
Evolution of shock-accelerated double-layer gas cylinder.
Physics of Fluids,
Vol. 33,
Issue. 8,
Liang, Yu
and
Luo, Xisheng
2021.
On shock-induced heavy-fluid-layer evolution.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Li, Jianming
Ding, Juchun
Luo, Xisheng
and
Zou, Liyong
2022.
Instability of a heavy gas layer induced by a cylindrical convergent shock.
Physics of Fluids,
Vol. 34,
Issue. 4,
Liang, Yu
2022.
The phase effect on the Richtmyer–Meshkov instability of a fluid layer.
Physics of Fluids,
Vol. 34,
Issue. 3,
Liang, Yu
2022.
Fundamental Studies of Shock-Driven Hydrodynamic Instabilities.
p.
1.
Zheng, Chun
He, Yong
Zhang, Huanhao
and
Chen, Zhihua
2022.
Effects of the parameters of inner air cylinder on evolution of annular SF6 cylinder accelerated by a planar shock wave.
Physics of Fluids,
Vol. 34,
Issue. 12,
Dang, Zi-Han
Zheng, Chun
Zhang, Huan-Hao
and
Chen, Zhi-Hua
2022.
Evolution mechanism of double-layer heavy gas column interface with sinusoidal disturbance induced by convergent shock wave.
Acta Physica Sinica,
Vol. 71,
Issue. 21,
p.
214703.
Liang, Yu
and
Luo, Xisheng
2022.
On shock-induced evolution of a gas layer with two fast/slow interfaces.
Journal of Fluid Mechanics,
Vol. 939,
Issue. ,
Liang, Yu
and
Luo, Xisheng
2022.
On shock-induced light-fluid-layer evolution.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Yan, Zheng
Fu, Yaowei
Wang, Lifeng
Yu, Changping
and
Li, Xinliang
2022.
Effect of chemical reaction on mixing transition and turbulent statistics of cylindrical Richtmyer–Meshkov instability.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Zhang, Duo
Ding, Juchun
Si, Ting
and
Luo, Xisheng
2023.
Divergent Richtmyer–Meshkov instability on a heavy gas layer.
Journal of Fluid Mechanics,
Vol. 959,
Issue. ,
Wang, Tao
Zhong, Min
Wang, Bing
Li, Ping
and
Bai, Jingsong
2023.
Evolution of turbulent mixing driven by implosion in spherical geometry.
Journal of Turbulence,
Vol. 24,
Issue. 9-10,
p.
419.
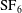 $\text{SF}_{6}$ layer surrounded by air is experimentally studied in a semi-annular convergent shock tube by high-speed schlieren photography. The gas layer with a sinusoidal outer interface and a circular inner interface is realized by the soap-film technique such that the initial condition is well controlled. Results show that the thicker the gas layer, the weaker the interface–coupling effect and the slower the evolution of the outer interface. Induced by the distorted transmitted shock and the interface coupling, the inner interface exhibits a slow perturbation growth which can be largely suppressed by reducing the layer thickness. After the reshock, the inner perturbation increases linearly at a growth rate independent of the initial layer thickness as well as of the outer perturbation amplitude and wavelength, and the growth rate can be well predicted by the model of Mikaelian (Physica D, vol. 36, 1989, pp. 343–357) with an empirical coefficient of 0.31. After the linear stage, the growth rate decreases continuously, and finally the perturbation freezes at a constant amplitude caused by the successive stagnation of spikes and bubbles. The convergent geometry constraint as well as the very weak compressibility at late stages are responsible for this instability freeze-out.
$\text{SF}_{6}$ layer surrounded by air is experimentally studied in a semi-annular convergent shock tube by high-speed schlieren photography. The gas layer with a sinusoidal outer interface and a circular inner interface is realized by the soap-film technique such that the initial condition is well controlled. Results show that the thicker the gas layer, the weaker the interface–coupling effect and the slower the evolution of the outer interface. Induced by the distorted transmitted shock and the interface coupling, the inner interface exhibits a slow perturbation growth which can be largely suppressed by reducing the layer thickness. After the reshock, the inner perturbation increases linearly at a growth rate independent of the initial layer thickness as well as of the outer perturbation amplitude and wavelength, and the growth rate can be well predicted by the model of Mikaelian (Physica D, vol. 36, 1989, pp. 343–357) with an empirical coefficient of 0.31. After the linear stage, the growth rate decreases continuously, and finally the perturbation freezes at a constant amplitude caused by the successive stagnation of spikes and bubbles. The convergent geometry constraint as well as the very weak compressibility at late stages are responsible for this instability freeze-out.



