Article contents
The bypass transition mechanism of the Stokes boundary layer in the intermittently turbulent regime
Published online by Cambridge University Press: 27 May 2020
Abstract
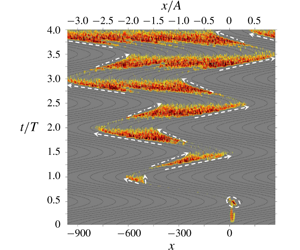
This numerical study focuses on the coherent structures and bypass transition mechanism of the Stokes boundary layer in the intermittently turbulent regime. In particular, the initial disturbance is produced by a temporary roughness element that is removed immediately after triggering a two-dimensional vortex tube under an inflection-point instability. The present study reveals a complete scenario of self-induced motion of a vortex tube after rollup from the boundary layer. The trajectory of the vortex tube is reasonably described based on the Helmholtz point-vortex equation. The three-dimensional transition of the vortex tube is attributed to the Crow instability, which leads to a sinusoidal disturbance that eventually evolves into a ring-like structure, especially for the weaker vortex. Further investigation demonstrates that three-dimensional or quasi-three-dimensional vortex perturbations in the free stream play a critical role in the boundary layer transition through a bypass mechanism, which is featured by the non-modal and explosive transient growth of the subsequent boundary layer instabilities. This transition scenario is found to be analogous to the oblique transition in the steady boundary layer, both of which are characterised by the formation of streaks, rollup of hairpin-like vortices and burst into turbulent spots. In addition, the streamwise propagation of turbulent spots is discussed in detail. To shed more light on the nature of the intermittently turbulent Stokes boundary layer, a conceptual model is proposed for the periodically self-sustaining mechanism of the turbulent spots based on the present numerical results and experimental evidence reported in the literature.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
Xiong et al. supplementary movie 1
(fig. 18) The video illustrating the propagation of turbulent spots in the moving reference frame $\hat{S}$. Case 16, $Re = 600$ and $h=0.5$.
- 8
- Cited by




