Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Guo, Xu
Zhai, Zhigang
Si, Ting
and
Luo, Xisheng
2019.
Bubble merger in initial Richtmyer-Meshkov instability on inverse-chevron interface.
Physical Review Fluids,
Vol. 4,
Issue. 9,
Desjardins, T.R.
Di Stefano, C.A.
Day, T.
Schmidt, D.
Merritt, E.C.
Doss, F.W.
Flippo, K.A.
Cardenas, T.
DeVolder, B.
Donovan, P.
Edwards, S.
Fierro, F.
Gonzales, R.
Goodwin, L.
Hamilton, C.
Quintana, T.
Randolph, R.
Rasmus, A.M.
Sedillo, T.
Wilson, C.
and
Welser-Sherrill, L.
2019.
A platform for thin-layer Richtmyer-Meshkov at OMEGA and the NIF.
High Energy Density Physics,
Vol. 33,
Issue. ,
p.
100705.
Cobos-Campos, F.
and
Wouchuk, J. G.
2019.
Analytic solution for the zero-order postshock profiles when an incident planar shock hits a planar contact surface.
Physical Review E,
Vol. 100,
Issue. 3,
Luo, Xisheng
Li, Ming
Ding, Juchun
Zhai, Zhigang
and
Si, Ting
2019.
Nonlinear behaviour of convergent Richtmyer–Meshkov instability.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
130.
Liang, Yu
Zhai, Zhigang
Ding, Juchun
and
Luo, Xisheng
2019.
Richtmyer–Meshkov instability on a quasi-single-mode interface.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
729.
Carter, John
Pathikonda, Gokul
Jiang, Naibo
Felver, Josef J.
Roy, Sukesh
and
Ranjan, Devesh
2019.
Time-Resolved Measurements of Turbulent Mixing in Shock-Driven Variable-Density Flows.
Scientific Reports,
Vol. 9,
Issue. 1,
Huang, Shenghong
Xu, Jianyu
Luo, Yifan
Sun, Pengyue
Luo, Xisheng
and
Ding, Juchun
2020.
Smoothed particle hydrodynamics simulation of converging Richtmyer–Meshkov instability.
Physics of Fluids,
Vol. 32,
Issue. 8,
Liang, Yu
Zhai, Zhigang
Luo, Xisheng
and
Wen, Chih-yung
2020.
Interfacial instability at a heavy/light interface induced by rarefaction waves.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
Mansoor, M. M.
Dalton, S. M.
Martinez, A. A.
Desjardins, T.
Charonko, J. J.
and
Prestridge, K. P.
2020.
The effect of initial conditions on mixing transition of the Richtmyer–Meshkov instability.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Sun, Rui
Ding, Juchun
Zhai, Zhigang
Si, Ting
and
Luo, Xisheng
2020.
Convergent Richtmyer–Meshkov instability of heavy gas layer with perturbed inner surface.
Journal of Fluid Mechanics,
Vol. 902,
Issue. ,
Guan, Ben
Wang, Dayi
Wang, Ge
Fan, E.
and
Wen, Chih-Yung
2020.
Numerical study of the Richtmyer–Meshkov instability of a three-dimensional minimum-surface featured SF6/air interface.
Physics of Fluids,
Vol. 32,
Issue. 2,
Liang, Yu
Liu, Lili
Zhai, Zhigang
Si, Ting
and
Wen, Chih-Yung
2020.
Evolution of shock-accelerated heavy gas layer.
Journal of Fluid Mechanics,
Vol. 886,
Issue. ,
Li, Ming
Ding, Juchun
Zhai, Zhigang
Si, Ting
Liu, Naian
Huang, Shenghong
and
Luo, Xisheng
2020.
On divergent Richtmyer–Meshkov instability of a light/heavy interface.
Journal of Fluid Mechanics,
Vol. 901,
Issue. ,
Bury, Yannick
Graumer, Pierre
Jamme, Stéphane
and
Griffond, Jérôme
2020.
Turbulent transition of a gaseous mixing zone induced by the Richtmyer-Meshkov instability.
Physical Review Fluids,
Vol. 5,
Issue. 2,
Luo, Xisheng
Liu, Lili
Liang, Yu
Ding, Juchun
and
Wen, Chih-yung
2020.
Richtmyer–Meshkov instability on a dual-mode interface.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Sun, Pengyue
Ding, Juchun
Huang, Shenghong
Luo, Xisheng
and
Cheng, Wan
2020.
Microscopic Richtmyer–Meshkov instability under strong shock.
Physics of Fluids,
Vol. 32,
Issue. 2,
Zhou, Zhangbo
Ding, Juchun
Zhai, Zhigang
Cheng, Wan
and
Luo, Xisheng
2020.
Mode coupling in converging Richtmyer–Meshkov instability of dual-mode interface.
Acta Mechanica Sinica,
Vol. 36,
Issue. 2,
p.
356.
Guo, Xu
Zhai, Zhigang
Ding, Juchun
Si, Ting
and
Luo, Xisheng
2020.
Effects of transverse shock waves on early evolution of multi-mode chevron interface.
Physics of Fluids,
Vol. 32,
Issue. 10,
Probyn, M.G.
Williams, R.J.R.
Thornber, B.
Drikakis, D.
and
Youngs, D.L.
2021.
2D single-mode Richtmyer–Meshkov instability.
Physica D: Nonlinear Phenomena,
Vol. 418,
Issue. ,
p.
132827.
Dimonte, Guy
2021.
A modal wave-packet model for the multi-mode Richtmyer–Meshkov instability.
Physics of Fluids,
Vol. 33,
Issue. 1,
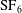 $\text{SF}_{6}$ interface are carried out at weak shock conditions. The soap-film technique is extended to create single-mode gaseous interfaces which are free of small-wavelength perturbations, diffusion layers and three-dimensionality. The interfacial morphologies captured show that the instability evolution evidently involves the smallest experimental uncertainty among all existing results. The performances of the impulsive model and other nonlinear models are thoroughly examined through temporal variations of the perturbation amplitude. The individual growth of bubbles or spikes demonstrates that all nonlinear models can provide a reliable forecast of bubble development, but only the model of Zhang & Guo (J. Fluid Mech., vol. 786, 2016, pp. 47–61) can reasonably predict spike development. The distinct images of the interface morphology obtained also provide a rare opportunity to extract interface contours such that a spectral analysis of the interfacial contours can be performed, which realizes the first direct validation of the high-order nonlinear models of Zhang & Sohn (Phys. Fluids, vol. 9, 1997, pp. 1106–1124) and Vandenboomgaerde et al. (Phys. Fluids, vol. 14 (3), 2002, pp. 1111–1122) in terms of the fundamental mode and high-order harmonics. It is found that both models show a very good and almost identical accuracy in predicting the first two modes. However, the model of Zhang & Sohn (1997) becomes much more accurate in modelling the third-order harmonics due to the fewer simplifications used.
$\text{SF}_{6}$ interface are carried out at weak shock conditions. The soap-film technique is extended to create single-mode gaseous interfaces which are free of small-wavelength perturbations, diffusion layers and three-dimensionality. The interfacial morphologies captured show that the instability evolution evidently involves the smallest experimental uncertainty among all existing results. The performances of the impulsive model and other nonlinear models are thoroughly examined through temporal variations of the perturbation amplitude. The individual growth of bubbles or spikes demonstrates that all nonlinear models can provide a reliable forecast of bubble development, but only the model of Zhang & Guo (J. Fluid Mech., vol. 786, 2016, pp. 47–61) can reasonably predict spike development. The distinct images of the interface morphology obtained also provide a rare opportunity to extract interface contours such that a spectral analysis of the interfacial contours can be performed, which realizes the first direct validation of the high-order nonlinear models of Zhang & Sohn (Phys. Fluids, vol. 9, 1997, pp. 1106–1124) and Vandenboomgaerde et al. (Phys. Fluids, vol. 14 (3), 2002, pp. 1111–1122) in terms of the fundamental mode and high-order harmonics. It is found that both models show a very good and almost identical accuracy in predicting the first two modes. However, the model of Zhang & Sohn (1997) becomes much more accurate in modelling the third-order harmonics due to the fewer simplifications used.

